Знакопостоянные ряды. Общее условие сходимости рядов с положительными членами.
Ряд 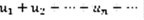 (1) называется знакопостоянным, если все его члены
(1) называется знакопостоянным, если все его члены 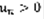 , либо если все его члены
, либо если все его члены 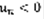 . Т.к. умножение ряда на (-1) не влияет на сходимость ряда, то в дальнейшем можно считать, что ряд (1) с положительными членами
. Т.к. умножение ряда на (-1) не влияет на сходимость ряда, то в дальнейшем можно считать, что ряд (1) с положительными членами 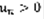 . Теорема 1: Общее условие сходимости рядов с положительными членами: для того, чтобы ряд (1) был сходящимся, необходимо и достаточно, чтобы все его частичные суммы
. Теорема 1: Общее условие сходимости рядов с положительными членами: для того, чтобы ряд (1) был сходящимся, необходимо и достаточно, чтобы все его частичные суммы 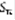 были ограничены сверху неким числом A.
были ограничены сверху неким числом A. 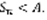 Док-во: Пусть ряд (1) сходящийся, S – сумма. (3) выполняется, если в качестве A взять S. Пусть (3) выполнено, т.к. члены ряда (1) – положительные, то его частичную сумму образует последовательность
Док-во: Пусть ряд (1) сходящийся, S – сумма. (3) выполняется, если в качестве A взять S. Пусть (3) выполнено, т.к. члены ряда (1) – положительные, то его частичную сумму образует последовательность 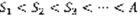 . Существует
. Существует 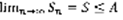 , значит все пределы сходящиеся.
, значит все пределы сходящиеся.
6. Признаки сравнения (в непредельной и предельной формах).
В непредельной форме: Рассмотрим два ряда с положительными членами: 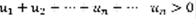 (1)
(1) 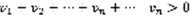 (2). Теорема 2: Предположим, что при всех натуральных n выполняется неравенство
(2). Теорема 2: Предположим, что при всех натуральных n выполняется неравенство 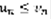 (3), тогда: 1) если (2) сходится, то и (1) сходится, 2)если (1) расходится, то (2) расходится. Док-во: Пусть (2) сходится, по Т1 (Общее условие сходимости рядов с положительными членами) тогда его частичные суммы
(3), тогда: 1) если (2) сходится, то и (1) сходится, 2)если (1) расходится, то (2) расходится. Док-во: Пусть (2) сходится, по Т1 (Общее условие сходимости рядов с положительными членами) тогда его частичные суммы 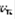 ограничены сверху некоторым числом A, т.е.
ограничены сверху некоторым числом A, т.е. 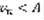 (4). Обозначим через
(4). Обозначим через 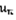 частичную сумму ряда (1) В силу (3)
частичную сумму ряда (1) В силу (3) 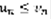 (5), по Т1 – ряд сходящийся. В предельной форме:
(5), по Т1 – ряд сходящийся. В предельной форме: 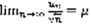 (6). Если
(6). Если 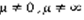 , тогда (1) и (2) сходятся или расходятся одновременно.
, тогда (1) и (2) сходятся или расходятся одновременно.  . Выберем два числа
. Выберем два числа 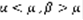 . Существует номер N такой, что для всех номеров
. Существует номер N такой, что для всех номеров 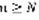 будет выполняться неравенство:
будет выполняться неравенство: 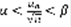 (7). Умножим
(7). Умножим 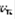 , тогда:
, тогда: 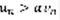 (8)
(8) 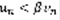 (9). Итак, пусть ряд (2) сходится, тогда сходится его N-ный остаток, значит сходится и ряд вида
(9). Итак, пусть ряд (2) сходится, тогда сходится его N-ный остаток, значит сходится и ряд вида 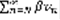 . В силу неравенства (9) следует, что по Т2, что будет сходиться и N-ный остаток ряда (1), а значит сходится и сам ряд (1). Пусть (2) расходится => N-ный остаток значит тоже расходится и ряд вида:
. В силу неравенства (9) следует, что по Т2, что будет сходиться и N-ный остаток ряда (1), а значит сходится и сам ряд (1). Пусть (2) расходится => N-ный остаток значит тоже расходится и ряд вида: 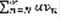 => будет расходиться N-ый остаток ряда (1), а значит и сам ряд (1) расходится. Замечание: признак сходимости в предельной форме обычно применяют в случае, когда N член ряда (1) имеет
=> будет расходиться N-ый остаток ряда (1), а значит и сам ряд (1) расходится. Замечание: признак сходимости в предельной форме обычно применяют в случае, когда N член ряда (1) имеет 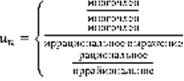 . В качестве ряда сравнения (2) берется такой ряд:
. В качестве ряда сравнения (2) берется такой ряд: 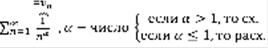
7. Признак Даламбера (в непредельной и предельной формах)
: Рассмотрим два ряда с положительными членами: 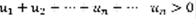 (1)
(1) 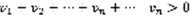 (2). Лемма: Если при всех
(2). Лемма: Если при всех 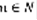 выполняется
выполняется 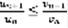 (3). Тогда: 1) если (2) расходится, то (1) тоже , 2) если (1) расходится, то (2) тоже. Доказательство: запишем (3) для различных n , начиная с n=1.
(3). Тогда: 1) если (2) расходится, то (1) тоже , 2) если (1) расходится, то (2) тоже. Доказательство: запишем (3) для различных n , начиная с n=1. 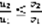 ,
, 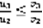 ,
, 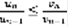 ,
, 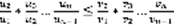 ,
, 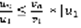 ,
, 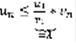 . Если (2) сходится, тогда и сходится
. Если (2) сходится, тогда и сходится 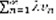 =>(1) сходится. Признак Даламбера в предельной форме: 1)Если при всех
=>(1) сходится. Признак Даламбера в предельной форме: 1)Если при всех 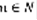 выполняются неравенства
выполняются неравенства 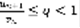 (5), то ряд (1) сходится. Теорема: Если при всех
(5), то ряд (1) сходится. Теорема: Если при всех 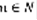 выполняются неравенства
выполняются неравенства 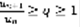 (6), то ряд (1) расходится. Доказательство 1: Рассмотрим геометрическую прогрессию вида:
(6), то ряд (1) расходится. Доказательство 1: Рассмотрим геометрическую прогрессию вида: 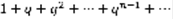 (7)
(7) 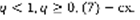
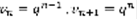 .
. 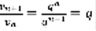 ,
, 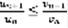 (8). Т.к. ряд (7) сходящийся и выполнено (8), то по Лемме, ряд (1) – сходящийся. Док-во 2:
(8). Т.к. ряд (7) сходящийся и выполнено (8), то по Лемме, ряд (1) – сходящийся. Док-во 2: 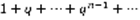 (9) ,
(9) , 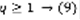 – расходящийся.
– расходящийся. 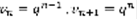 ,
, 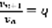 ,
, 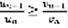 (10). На основании Леммы – ряд расходящийся. Теорема: пусть существует предел
(10). На основании Леммы – ряд расходящийся. Теорема: пусть существует предел 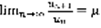 . 1)Если
. 1)Если 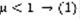 -сходящийся, 2)Если
-сходящийся, 2)Если 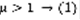 -расходящийся, 3)Если
-расходящийся, 3)Если  теорема ничего не утверждает. Док-во: 1)
теорема ничего не утверждает. Док-во: 1) 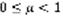 . Выберем q так, чтобы q:
. Выберем q так, чтобы q: 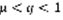 . Существует N,
. Существует N, 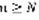 .
. 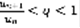 (11). На основании Т1 оттуда следует, что n-ый остаток ряда (1) сходится. 2) q:
(11). На основании Т1 оттуда следует, что n-ый остаток ряда (1) сходится. 2) q: 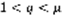 Существует номер N, такой, что для всех номеров, начиная с него
Существует номер N, такой, что для всех номеров, начиная с него 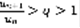 по Т1. N-ый остаток ряда (1) расходится.
по Т1. N-ый остаток ряда (1) расходится.
8. Интегральный признак Коши. Сходимость обобщенно гармонических рядов.
Рассмотрим ряд с положительными членами: 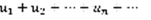 (1). Предположим дополнительно, что члены ряда (1) убывают с ростом номера.
(1). Предположим дополнительно, что члены ряда (1) убывают с ростом номера. 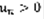 ,
, 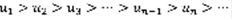 (2). Определение: функцией Коши, соответствующей ряду (1) называется числовая функция вещественной переменной x f(x), которая определена для
(2). Определение: функцией Коши, соответствующей ряду (1) называется числовая функция вещественной переменной x f(x), которая определена для 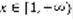 и обладает следующими свойствами: 1) f(x) – непрерывна 2)f(x) –убывает 3)
и обладает следующими свойствами: 1) f(x) – непрерывна 2)f(x) –убывает 3) 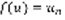 . Теорема: Пусть функция f(x) – функция Коши ряда (1), тогда сходимость ряда (1) эквивалентна сходимости несобственного интеграла. Сх-ть (1)
. Теорема: Пусть функция f(x) – функция Коши ряда (1), тогда сходимость ряда (1) эквивалентна сходимости несобственного интеграла. Сх-ть (1) 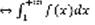 (3).
(3). 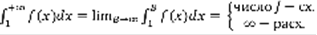 .
. 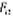 – площадь криволинейной трапеции под графиком функции f(x) с основанием от 1 до n.
– площадь криволинейной трапеции под графиком функции f(x) с основанием от 1 до n. 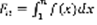 (4).
(4). 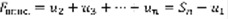 ,
, 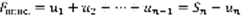 .
. 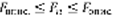 ,
, 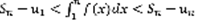 (5) ,
(5) , 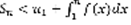 (6) ,
(6) , 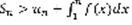 (7). Пусть (1) сходится, значит существует
(7). Пусть (1) сходится, значит существует 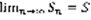 . Существует
. Существует 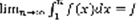 –число =>сходящийся. Пусть (1) –расходящийся, значит
–число =>сходящийся. Пусть (1) –расходящийся, значит 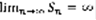 ,
, 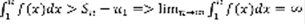 -расходящийся. Гармонический ряд:
-расходящийся. Гармонический ряд: 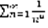 ,
, 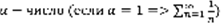 – гармонический ряд. Ряд расходящийся, если
– гармонический ряд. Ряд расходящийся, если 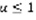 , сходящийся, если
, сходящийся, если 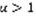 .
.
9. Знакочередующиеся ряды. Признак сходимости Лейбница.
Это ряд вида 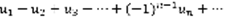 (1)
(1) 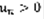 . Теорема: признак сходимости: пусть выполнены два условия: 1)Члены ряда (1) убывают по абсолютной величине с ростом номера. 2)
. Теорема: признак сходимости: пусть выполнены два условия: 1)Члены ряда (1) убывают по абсолютной величине с ростом номера. 2) 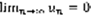 . Тогда ряд (1) сходится. Док-во: обозначим
. Тогда ряд (1) сходится. Док-во: обозначим 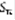 – n-ая частичная сумма ряда (1).
– n-ая частичная сумма ряда (1). 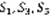 – частичная сумма с учетом номера.
– частичная сумма с учетом номера. 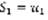 ,
,  ,
, 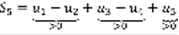 . 1)
. 1) 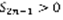 2)Покажем, что эти частичные суммы уменьшаются с ростом номера:
2)Покажем, что эти частичные суммы уменьшаются с ростом номера: 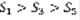 ,
, 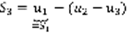 ,
, 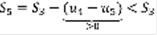 . Существует предел:
. Существует предел: 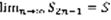 ,
, 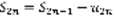 ,
, 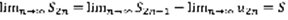 => Если
=> Если 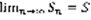 – ряд расходящийся. Если
– ряд расходящийся. Если 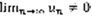 => (1) – расходящийся.
=> (1) – расходящийся.
10. Сходимость ряда при условии сходимости ряда абсолютных величин его членов. Абсолютно и не абсолютно сходящиеся ряды. Основные свойства абсолютно сходящихся рядов.
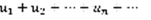 (1) не делая никаких предположений относительно знаков его членов. Такой ряд называется знакопеременным рядом. Рассмотрим
(1) не делая никаких предположений относительно знаков его членов. Такой ряд называется знакопеременным рядом. Рассмотрим 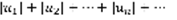 (2) – с положительными членами.
(2) – с положительными членами. 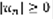 . Лемма: пусть n-вещественное число, тогда: 1) Если взять абсолютную величину числа, добавить или вычесть его, разделить на 2, будет
. Лемма: пусть n-вещественное число, тогда: 1) Если взять абсолютную величину числа, добавить или вычесть его, разделить на 2, будет 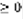 .
. 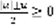 (3) . 2)
(3) . 2) 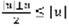 (4) . Теорема: Если (2) сходится, то (1) тоже сходится. Рассмотрим 2 вспомогательных ряда:
(4) . Теорема: Если (2) сходится, то (1) тоже сходится. Рассмотрим 2 вспомогательных ряда: 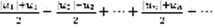 (5)
(5) 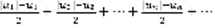 (6). На основании леммы
(6). На основании леммы 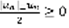 , значит, ряды (5) и (6) с неотрицательными членами. На основании той же леммы
, значит, ряды (5) и (6) с неотрицательными членами. На основании той же леммы 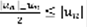 . То есть, члены рядов (5) и (6) не превосходят членов ряда (2). Т.к. ряд (2) – сходящийся, то по признаку сравнения рядов с положительными членам, ряды (5) и (6) тоже сходящиеся. Сходящиеся ряды можно почленно вычитать, при этом получится снова сходящийся ряд (5)-(6). Ряд (1) – сходящийся. Утверждение, обратное теореме неверно, из сходимости ряда (1) не следует сходимость ряда (2). При исследовании сходимости рядов (1) и (2) возможны следующие случаи: 1) Ряд (2) сходящийся, тогда по Теореме ряд (1) тоже сходится. Ряд (1) называется абсолютно сходящимся. 2)Ряд (2) – расходящийся, а ряд (1) – сходящийся. Ряд (1) называется не абсолютно (условно) сходящимся. 3) Ряд (1) –расх. ((2)-расх.). Свойства абсолютно сходящихся рядов: 1)пусть ряд (1) – абсолютно сходящийся и имеет сумму S, тогда в таком ряде можно произвольным образом менять порядок следования слагаемых, при этом полученный ряд снова будет абсолютно сходящийся и имеет сумму S. 2) Пусть ряд (1) абсолютно сходящийся и имеет сумму S. И имеется еще один абсолютно сходящийся ряд
. То есть, члены рядов (5) и (6) не превосходят членов ряда (2). Т.к. ряд (2) – сходящийся, то по признаку сравнения рядов с положительными членам, ряды (5) и (6) тоже сходящиеся. Сходящиеся ряды можно почленно вычитать, при этом получится снова сходящийся ряд (5)-(6). Ряд (1) – сходящийся. Утверждение, обратное теореме неверно, из сходимости ряда (1) не следует сходимость ряда (2). При исследовании сходимости рядов (1) и (2) возможны следующие случаи: 1) Ряд (2) сходящийся, тогда по Теореме ряд (1) тоже сходится. Ряд (1) называется абсолютно сходящимся. 2)Ряд (2) – расходящийся, а ряд (1) – сходящийся. Ряд (1) называется не абсолютно (условно) сходящимся. 3) Ряд (1) –расх. ((2)-расх.). Свойства абсолютно сходящихся рядов: 1)пусть ряд (1) – абсолютно сходящийся и имеет сумму S, тогда в таком ряде можно произвольным образом менять порядок следования слагаемых, при этом полученный ряд снова будет абсолютно сходящийся и имеет сумму S. 2) Пусть ряд (1) абсолютно сходящийся и имеет сумму S. И имеется еще один абсолютно сходящийся ряд  и имеет сумму T. Тогда при почленном перемножении рядов (1) и (7) получится абсолютно сходящийся ряд с суммой =S*T.
и имеет сумму T. Тогда при почленном перемножении рядов (1) и (7) получится абсолютно сходящийся ряд с суммой =S*T. 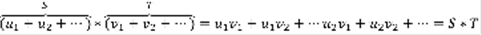 . Теорема Римана: пусть ряд (1) – условно сходящийся, тогда: 1)за счет перестановки членов ряда (1) можно получить либо ряд расходящийся, либо ряд сходящийся, но сумма которого не равна сумме исходного ряда. 2) Существует два условно сходящихся ряда (1) и (7), для которого их почленное произведение окажется либо расходящимся рядом, либо сходящимся, но суммой, не равной S*T. Если в ряде (1) все
. Теорема Римана: пусть ряд (1) – условно сходящийся, тогда: 1)за счет перестановки членов ряда (1) можно получить либо ряд расходящийся, либо ряд сходящийся, но сумма которого не равна сумме исходного ряда. 2) Существует два условно сходящихся ряда (1) и (7), для которого их почленное произведение окажется либо расходящимся рядом, либо сходящимся, но суммой, не равной S*T. Если в ряде (1) все 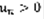 , то
, то  , то есть ряд (2) = (1) и для таких рядов понятие сходимости совпадает с понятием абсолютной сходимости.
, то есть ряд (2) = (1) и для таких рядов понятие сходимости совпадает с понятием абсолютной сходимости.
