Представление «обобщенного» вектора на комплексной плоскости

Обобщенный вектор, как и любой вектор на комплексной плоскости, можно представить алгебраической формой записи комплексного числа.

Обычно это делают, совмещая вещественную ось с осью обмотки в фазе «А».

Тогда 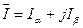. (55)

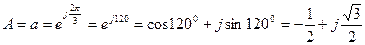. (56)

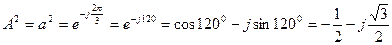. (57)

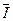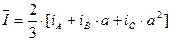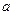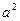Подставляя в выражение для ( ) значения операторов поворота и , записанные в алгебраической форме, и разделяя вещественную и мнимую части получим

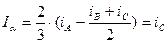. (58)

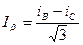. (59)

Переход от представления обобщенного вектора 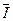через проекции на оси трехфазных обмоток к представлению через проекции на оси комплексной плоскости эквивалентен преобразованию трехфазной системы обмоток в эквивалентную двухфазную.

В матричной форме преобразование от трехфазной системы обмоток к эквивалентной двухфазной можно записать в виде

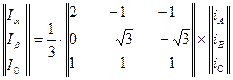. (60)

Обратное преобразование координат обобщенного вектора 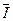от проекций на оси комплексной плоскости к представлению через проекции трехфазных обмоток осуществляется по следующей матричной формуле

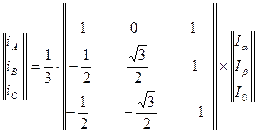. (61)

13.10. Преобразование «обобщенного» вектора на комплексной плоскости в разных системах координат

В соответствии с выражением (51) преобразование обобщенного вектора 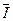, записанного в системе координат « 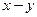», в вектор 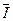, записанной в системе координат « 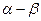», сдвинутой на угол « 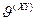» относительно системы координат « 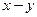», можно представить в развернутом виде следующим образом:

.

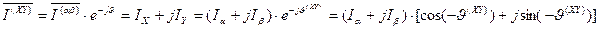Раскрывая скобки и преобразуя полученное алгебраическое выражение, получим:

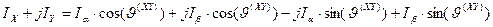. (62)

Приравнивая действительные и мнимые части в правой и левой частях выражения (62), получим:

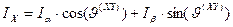. (63)

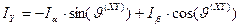. (64)

Можно также найти составляющие вектора 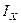и 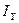в матричной форме.

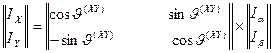. (65)

Обратное преобразование для определения проекций в системе координат « 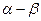» по известным проекциям в системе координат « 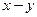» производится по следующей матричной формуле.

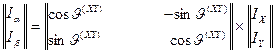. (66)

Обратное преобразование координат в развернутом виде выглядит в следующем виде.

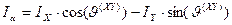. (67)

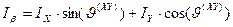. (68)

13.11. Преобразование «обобщенных» векторов потокосцеплений статора и ротора АД при записи в другой системе координат

В выражениях (47) и (48) для потокосцеплени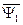й и 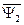векторы тока статора и ротора записаны в различных системах координат. Так, в выражении для потокосцепления 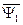ток статора записан в неподвижной системе координат « 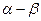», связанной со статором, а ток ротора во вращающейся системе координат « 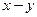», связанной с ротором (смещенной на текущий угол « 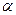» ). Полная запись выражения для потокосцепления 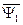с учетом индексов систем координат выглядит следующим образом.

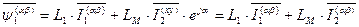. (69)

Если обе части выражения (69) умножить на оператор поворота 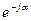, то получим:

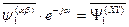. (70)

Запишем выражение (70) в развернутом виде с учетом выражения (51).

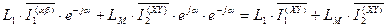. (71)

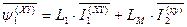. (72)

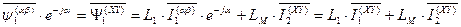. (73)

Тогда окончательно потокосцепления статора с учетом всех токов АД и независимо от выбранной системы координат можно представить в виде

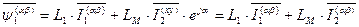. (74)

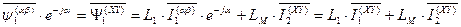. (75)

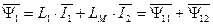. (76)

По аналогии также можно записать потокосцепления ротора с учетом всех токов АД независимо от выбранной системы координат.

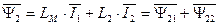. (77)

В уравнениях (76) и (77) все коэффициенты являются постоянными величинами и не зависят от взаимного расположения обмоток статора и ротора, т.к токи статора и ротора записаны в одной и той же системе координат.

Из выражений следует, что потокосцепления статора и ротора раскладываются на составляющие, обусловленные собственным током ( 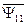и 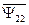) и током другой части АД ( 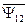и ).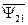

Пользуясь тем, что сумма токов статора и ротора образует ток намагничивания АД (см. рис. 12), т.е. 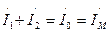, потокосцепления статора 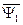и ротора 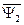можно также представить через потокосцепление основного магнитного потока 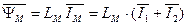и потокосцепления рассеяния статора 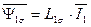и ротора .

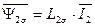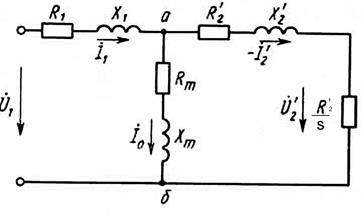
Рис. 12. Схема замещения АД

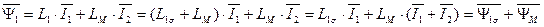. (78)

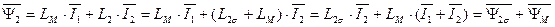. (79)

13.12. Преобразование уравнений статора и ротора для записи в общей системе координат

Уравнения для цепи статора и ротора с применением обобщенных векторов тока, напряжения и потокосцепления имеют следующий вид.

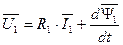. (80)

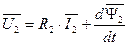. (81)

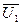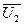Уравнения для и записаны в разных системах координат. Уравнение для статорной цепи 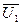записано в неподвижной системе координат с осями 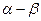. Уравнение для роторной цепи 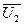записано во вращающейся системе координат с осями 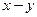. Для перевода и записи уравнения для роторной цепи 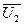в неподвижной системе координат « 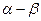» умножим обе его части на оператор поворота 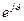. Умножение уравнения для 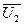на оператор поворота 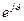осуществляет поворот системы координат « 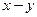» на текущий угол поворота 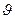. Представим в производной ( 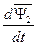) вектор потокосцепления ротора ( 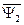) в системе координат « 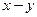» как 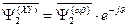. (82)

После преобразований с учетом выражения (82), опуская индексы координатной системы, получим уравнение ротора в векторной форме в системе координат статора « ».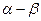

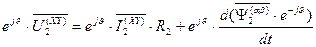. (83)

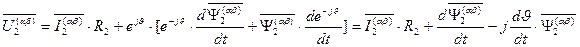. (84)

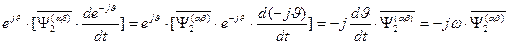. (85)

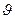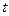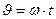Если угол поворота изменяется прямо пропорционально времени , т.е , то 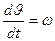– текущая скорость вращения ротора.

Таким образом, уравнение ротора в векторной форме в неподвижной системе координат статора « 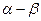» выглядит так.

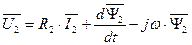. (86)