Вопрос 7.2. Базис на плоскости и в пространстве. Координаты вектора

Определение 7.6. Линейной комбинацией векторов

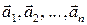
называется выражение вида

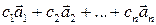
Числа

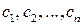
называются коэффициентами линейной комбинации.

Определение 7.7. Вектора

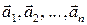
называются линейно независимыми, если их линейная комбинация равна нулевому вектору только тогда, когда все ее коэффициенты одновременно равны 0.

Определение 7.8. Вектора

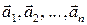
называются линейно зависимыми, если их линейная комбинация равна нулевому вектору хотя бы при одном не равном нулю коэффициенте.

Лемма 7.1. Если среди векторов есть нулевой вектор, то такие вектора являются линейно зависимыми.

Докажите лемму самостоятельно.

Определение 7.9. Базисом называются n линейно независимых векторов, таких, что любой вектор может быть представлен в виде их линейной комбинации. Коэффициенты этой линейной комбинации называются координатами вектора относительно данного базиса.

Теорема 7.1. Координаты вектора относительно данного базиса единственны.

Доказательство. Пусть вектор 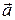разложен двумя способами по базису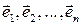

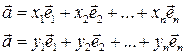
Вычтем из первого уравнения второе, тогда получим

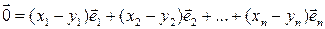
откуда, в силу линейной независимости базисных векторов, следуют равенства

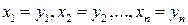
Конец доказательства.

Теорема 7.2. При сложении векторов их координаты складываются, а при вычитании ‑ вычитаются. При умножении на число координаты вектора умножаются на это число.

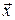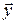Доказательство. Если вектора и разложены по базису, то

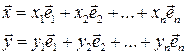
Складывая вектора 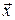и 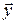, получим

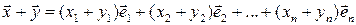
Аналогично доказываются два последних утверждения.

Конец доказательства.

Определение 7.10. Параллельные друг другу вектора называются коллинеарными.

Очевидно, что если вектора 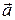и 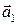коллинеарны, то 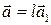. При этом 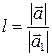, если вектора 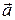и 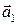одинаково направлены и 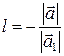в противном случае. Отсюда следует, что два коллинеарных вектора линейно зависимы, так как можно записать

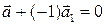
Справедливо обратное утверждение: два линейно зависимых вектора коллинеарны. Действительно, пусть

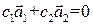
и, например, коэффициент 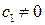, тогда

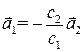
Из выше сказанного следует, что два неколлинеарных вектора линейно независимы.

Определение 7.11. Три вектора, параллельные одной и той же плоскости, называются компланарными.

Теорема 7.3. На плоскости любые два неколлинеарных вектора образуют базис.

Доказательство. Пусть даны два произвольных неколлинеарных вектора 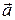и 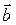, лежащие в одной плоскости. Покажем, что произвольный плоский вектор 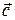можно разложить по этим векторам. Проведем через конец вектора 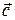две прямые, параллельные векторам 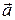и 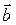. Тогда вектор 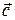есть сумма векторов 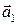и 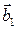(см. рис. 2).

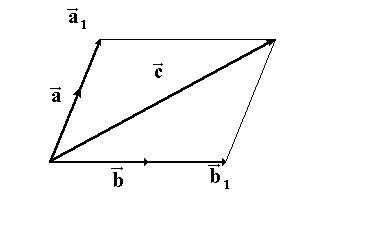
Рис. 2. К доказательству теоремы 3.

Но вектора 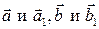коллинеарны, поэтому 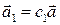и 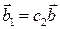. Тогда 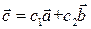. Кроме того, вектора 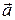и 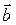как неколлинеарные линейно независимы. Таким образом, произвольный вектор 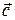разлагается по линейно независимым векторам 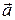и 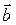. Следовательно, вектора 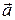и 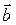образуют базис на плоскости.

Конец доказательства.

Можно доказать следующую теорему:

ТЕОРЕМА 7.4. В пространстве любые три некомпланарных вектора образуют базис.

Определение 7.12. Системой координат называется базис и выделенная точка (начало системы координат). Прямые, проходящие через начало системы координат параллельно базисным векторам, называются координатными осями.

Определение 7.13. Координатами точки M называются координаты радиус-вектора, соединяющего начало координат с точкой M.

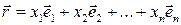
где 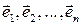‑ базис.

Пользуясь этим определением легко доказать теорему

Теорема 7.5. Координаты вектора 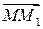равны разности координат его начала и конца.

Доказательство. Пусть 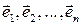‑ базис. Тогда, если точки 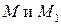соединяются радиус-векторами 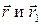, то 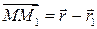. Разложим радиус-вектора по базису, тогда

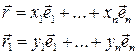
Или вычитая из второго равенства первое, получим

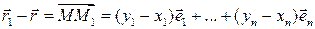
Что и требовалось доказать.

Конец доказательства.