Необходимый признак сходимости числового ряда.

Гармонический ряд.

Нахождение n -й частичной суммы 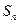и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости . Первым из них, как правило, является необходимый признак сходимости.

Теорема.

Если ряд 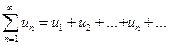сходится, то его общий член 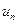стремится к нулю, т.е. .

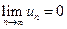Пусть ряд 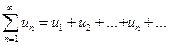сходится и 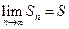. Тогда и 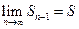. Учитывая, что 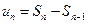при n>1 , получаем:

.

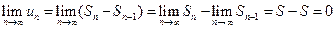Следствие (достаточное условие расходимости ряда)

Если 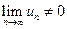или этот предел не существует, то ряд расходится.

Действительно, если бы ряд сходился, то (по теореме) 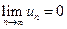. Но это противоречит условию. Значит, ряд расходится.

Теорема о сходимости дает необходимое условие сходимости ряда, но не достаточное: из условия 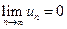не следует, что ряд сходится. Это означает, что существуют расходящиеся ряды, для которых .

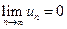В качестве примера рассмотрим так называемый гармонический ряд

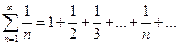
Очевидно, что 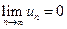. Однако ряд расходится.

Как известно, 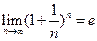. Отсюда следует, что при любом 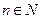имеет место неравенство 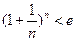. Логарифмируя это неравенство по основанию е , получим:

,

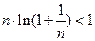т.е. ,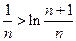

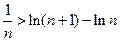
Подставляя в полученное неравенство поочередно n=1, 2, …, n – 1, n , получим:

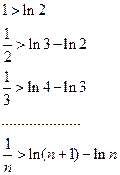
Сложив почленно эти неравенства, получаем 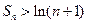. Поскольку 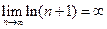, получаем 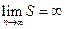, т.е. гармонический ряд 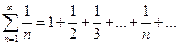расходится.

Достаточные признаки сходимости знакопостоянных рядов.

Необходимый признак сходимости не дает возможности судить о том, сходится ли данный ряд или нет. Сходимость и расходимость ряда во многих случаях можно установить с помощью так называемых достаточных признаков .

Рассмотрим некоторые из них для знакоположительных рядов, т.е. рядов с неотрицательными членами.

Признаки сравнения рядов.

Сходимость или расходимость знакоположительного ряда часто устанавливают путем сравнения его с другим рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.

Теорема1.

Пусть даны два знакоположительных ряда

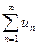
и

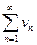
Если для всех n выполняется неравенство

,

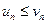то из сходимости ряда 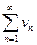следует сходимость ряда 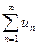, из расходимости ряда 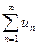следует расходимость ряда .

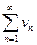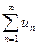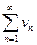Обозначим n -е частичные суммы рядов и соответственно через 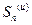и 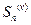. Из неравенства 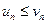следует, что

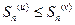
Пусть ряд 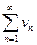сходится и его сумма равна 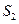. Тогда 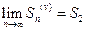. Члены ряда 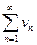положительны, поэтому 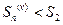и, следовательно, с учетом неравенства 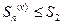. таким образом, последовательность 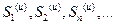( 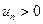) монотонно возрастает ( 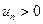) и ограничена сверху числом 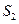. По признаку существования предела последовательность 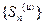имеет предел 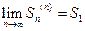, т.е. ряд 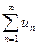сходится.

Пусть теперь ряд 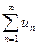расходится. Так как члены ряда неотрицательны, в этом случае имеем 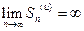. Тогда с учетом неравенства 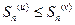получаем 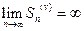, т.е. ряд 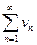расходится.

Теорема2 (предельный признак сравнения)

Пусть даны два знакоположительных ряда 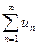и 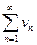. Если существует конечный, отличный от 0, предел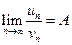 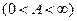, то ряды сходятся или расходятся одновременно.

По определению предела последовательности для всех n , кроме, возможно, конечного числа их, для любого 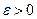выполняется неравенство 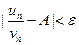, или .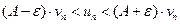

Если ряд 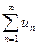сходится, то из левого неравенства 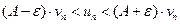и теоремы1 вытекает, что ряд 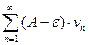также сходится. Но тогда, согласно свойству1 числовых рядов, ряд 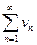сходится.

Если ряд 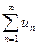расходится, то из правого неравенства 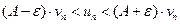, теоремы1, свойства 1 вытекает, что ряд 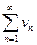расходится.

Аналогично, если ряд 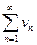сходится (расходится), то сходящимся (расходящимся) будет и ряд .

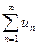Признак Даламбера

В отличии от признаков сравнения признак Даламбера позволяет часто решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом.

Теорема

Пусть дан ряд 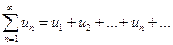с положительными членами и существует конечный или бесконечный предел .

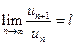Тогда ряд сходится при l<1 и расходится при l>1 .

Так как 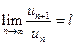, то по определению предела для любого 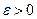найдется натуральное число N такое, что при n>N выполняется неравенство

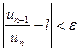или .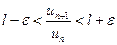

Пусть l<1 . Можно подобрать 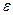так, что число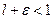 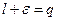, 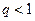. Обозначим 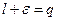, 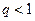. Тогда из правой части неравенства 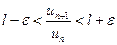получаем 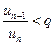, или 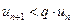. В силу свойства 3 числовых рядов можно считать, что 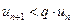для всех n=1, 2, 3,… Давая номеру n эти значения, получим серию неравенств:

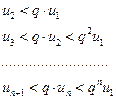
т.е. члены ряда 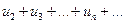меньше соответствующих членов ряда 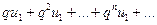, который сходится как ряд геометрической прогрессии со знаменателем 0<q<1 . Но тогда, на основании признака сравнения, сходится ряд 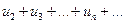, следовательно, сходится и исходный ряд .

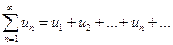Пусть l>1 . В этом случае 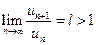. Отсюда следует, что начиная с некоторого номера N , выполняется неравенство 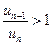, или 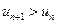, т.е. члены ряда возрастают с увеличением номера n . Поэтому 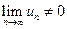. На основании следствия из необходимого признака ряд 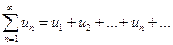расходится.

Если l=1 , то ряд 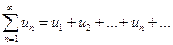может быть как сходящимся, так и расходящимся.

Радикальный признак Коши

Теорема.

Пусть дан ряд 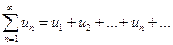с положительными членами и существует конечный или бесконечный предел 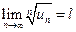. Тогда ряд сходится при 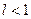и расходится при .

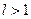Как и для признака Даламбера, в случае, когда l=1 , вопрос о сходимости ряда остается открытым. Доказательство теоремы аналогично доказательству признака Даламбера.

Интегральный признак Коши