Обобщенный гармонический ряд

Теорема .

Если члены знакоположительного ряда 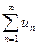могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке 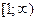функции 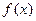так, что 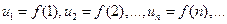, то:

1) если 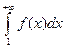сходится, то сходится и ряд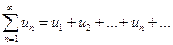

2) если 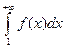расходится, то расходится также и ряд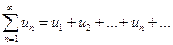

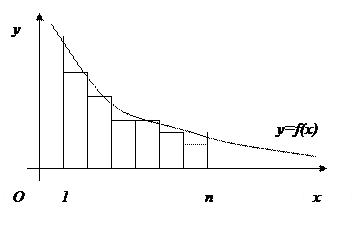
Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции y=f(x), основанием которой служит отрезок оси Ох от х=1 до х= n.

Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки [1;2],[2;3],... Учитывая геометрический смысл определенного интеграла, запишем:

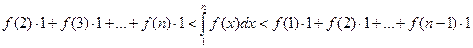
или

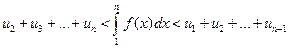
или

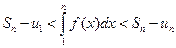
Случай 1 . Несобственный интеграл 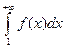сходится, т.е. 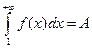. Поскольку 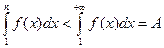, то с учетом неравенства 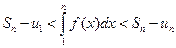имеем: 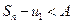, т.е. 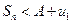. Так как последовательность частичных сумм монотонно возрастает и ограничена сверху (числом 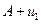), то, по признаку существования предела, имеет предел.

Следовательно, ряд 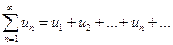сходится.

Случай 2. Несобственный интеграл 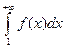расходится. Тогда 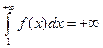и интегралы 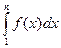неограниченно возрастают при 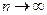. Учитывая, что 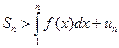, получаем, что 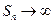при 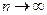. Следовательно, данный ряд 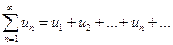расходится.

Ряд ,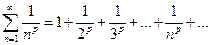

где p>0 – действительное число, называется обобщенным гармоническим рядом . Для исследования ряда на сходимость применим интегральный признак Коши.

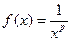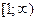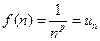Рассмотрим функцию . Эта функция непрерывна, монотонно убывает на промежутке и . При 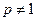имеем:

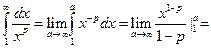
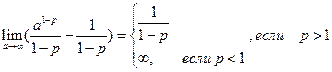
При p=1 имеем гармонический ряд 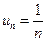, который расходится. Итак, ряд 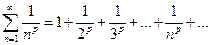сходится при 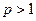, расходится при 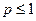. В частности, ряд 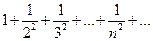сходится.

Знакочередующиеся и знакопеременные ряды

Знакочередующиеся ряды

Знакочередующимся рядом называется ряд вида

,

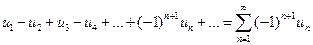где 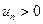для всех .

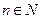Теорема(достаточный признак Лейбница сходимости знакочередующегося ряда).

Знакочередующийся ряд 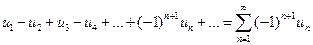сходится, если:

1. Последовательность абсолютных величин членов ряда монотонно убывает, т.е.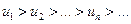

2. Общий член ряда стремится к нулю: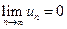

При этом сумма S ряда 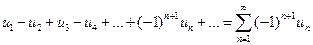удовлетворяет неравенствам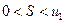

Рассмотрим сначала частичную сумму четного числа (2m ) членов ряда. Имеем

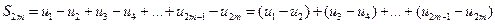
Выражение в каждой скобке, согласно первому условию теоремы, положительно. Следовательно, сумма 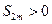и возрастает с возрастанием номера 2m.

С другой стороны, 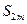можно переписать так:

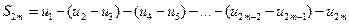
Легко видеть, что 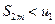. Таким образом, последовательность 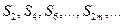возрастает и ограничена сверху. Следовательно, она имеет предел 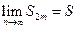, причем .

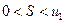Рассмотрим теперь частичные суммы нечетного числа ( 2m+1) членов ряда. Очевидно, что 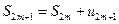. Отсюда следует, что 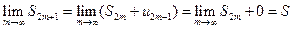, т.к. 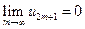в силу второго условия теоремы. Итак, 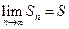как при четном n , так и при нечетном n . Следовательно, ряд 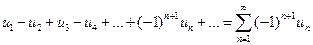сходится, причем .

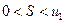Общий достаточный признак сходимости знакопеременных рядов

Знакочередующийся ряд является частным случаем знакопеременного ряда. Числовой ряд 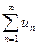, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называетсязнакопеременным.

Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема.

Пусть дан знакопеременный ряд

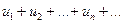
Если сходится ряд ,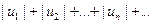

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд .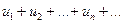

Рассмотрим вспомогательный ряд, составленный из членов рядов 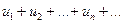и :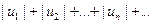

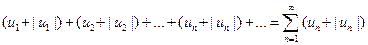
Очевидно, что 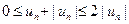для всех 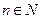. Но ряд 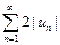сходится в силу условия теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд 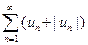. Поскольку данный знакопеременный ряд 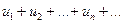представляет собой разность двух сходящихся рядов

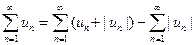
то, на основании свойства 2 числовых рядов, он сходится.

Обратное утверждение неверно.