Дифференцирование и интегрирование векторных функций

Пусть векторная функция r(t) определена на множестве {t}.

Говорят, что векторная функция r(t) имеет производную в точке t, если существует предел

lim (r(t+Dt)−r(t))/Dt при Dt ®0

Обозначения: r'(t)≡dr(t)/dt.

Геометрический смысл производной векторной функции ясен из рис. 11.

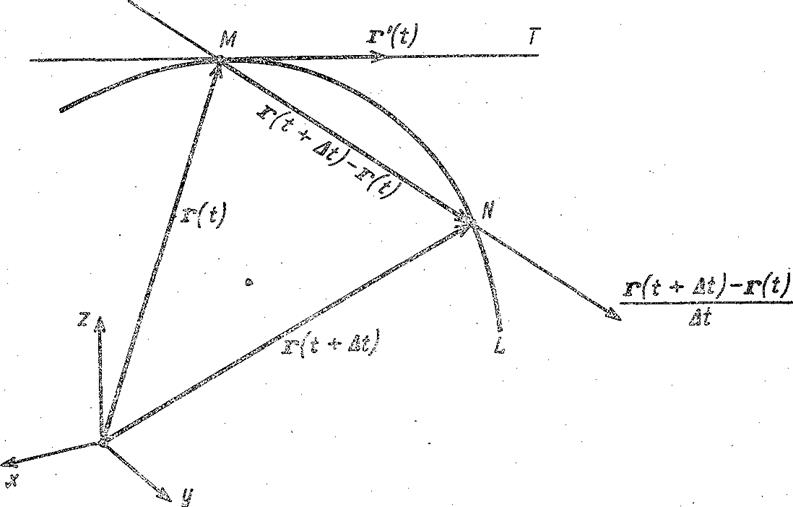
Рис. 11. Вектор r'(t) направлен по касательной к годографу векторной функции r=r(t) в точке М

Если r'(t)≠0, то существует касательная к годографу L векторной функции r(t) в точке М, отвечающей значению t параметра, и вектор r'(t) направлен по этой касательной.

Пусть j(t),y(t),χ(t) — координаты векторной функции r(t).

Если функция r(t) имеет производную в точке t, то каждая из функций j(t),y(t),χ(t) также имеет производную в точке t.

Верно и обратное: если функции j(t),y(t),χ(t) имеют производные в точке t, то и векторная функция r(t) имеет производную в этой точке.

Если каждая из функций r(t), R(t) и λ(t) имеет производную в точке t, то функции r(t)±R(t), λ(t)r(t), r(t)´R(t), r(t)•R(t)также имеют производные в этой точке, причем выполняются следующие соотношения:

(r ± R)' = r' ± R',(λ(t)r(t))' = λ(t)'r(t) + λ(t)r(t)',

Производная векторной функции r'(t) называется второй производной векторной функции r(t). Аналогично определяются третья и последующие производные.

Вторая и третья производные обозначаются соответственно через r"(t) и r'"(t).

Для производных n-го порядка обычно используются обозначения r⁽ⁿ⁾(t) или dⁿr(t)/dtⁿ.

Если j(t),y(t),χ(t) — координаты векторной функции r(t), то

r⁽ⁿ⁾(t) = j⁽ⁿ⁾(t)i+ y⁽ⁿ⁾(t)j+ χ⁽ⁿ⁾(t)k. (2)

Если у векторной функции r(t) существуют и непрерывны все производные до порядка n включительно, то пишут r(t)ÎCⁿ.

Пусть функция r(t)ÎC^n-1 в некоторой окрестности точки t₀ и существует производная rⁿ(t₀). Тогда для r(t) справедлива формула Тейлора[2]:

Формула (3) получается так.

Разложим координатные функции j(t),y(t),χ(t) вектора r(t) по формуле Тейлора с остаточным членом в форме Пеано[3] o((t-t₀)ⁿ)

Умножая первое соотношение на орт i, второе — на орт j, третье — на орт k, складывая и используя формулы (1) и (2), получим разложение (3).

Интеграл Римана 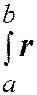(t)dt для векторной функции r(t), a£t£b, определяется как предел интегральных сумм.

Достаточные условия гладкости кривой

ТЕОРЕМА 1 (достаточные условия гладкости в точке).

Пусть кривая L задана векторной функцией r=r(t), имеющей в некоторой окрестности значения t₀Î{t} непрерывную производную r'(t), причем r'(t₀)≠0.

Тогда кривая L является гладкой кривой в точке М₀, отвечающей значению t₀.

ТЕОРЕМА 2 (достаточные условия гладкости кривой).

Пусть кривая L задана векторной функцией r=r(t), tÎ{t}, имеющей непрерывную производную r'(t). Если r'(t)≠0 для любого tÎ{t}, то кривая L гладкая.

Поскольку r'(t)≠0, то согласно теореме 1 кривая L является гладкой в любой своей точке. Из условия r'(t)≠0 и непрерывности r'(t) следует непрерывность касательной к кривой L. Значит, L — гладкая кривая.

Регулярные кривые

Пусть гладкая кривая L задана векторной функцией r=r(t). Если r(t)ÎCⁿ, n>2, то кривая L называется регулярной кривой (кривой класса С^п).

Достаточные условия регулярности кривой.

Для того чтобы заданная векторной функцией r(t), tÎ{t}, кривая L была регулярной, достаточно, чтобы на множестве {t} изменения параметра были выполнены следующие условия: r(t)ÎCⁿ, n>2, r'(t)≠0.

Эти условия вытекают из достаточных условий гладкости (теорема 2) и определения регулярности.

Замечание. Если производная r'(t) непрерывна и r'(t₀)≠0, то r'(t)≠0 в некоторой окрестности, значения t₀. Если, кроме того, r(t)ÎCⁿ, n>2, на множестве {t}, то в окрестности точки М₀, отвечающей значению t₀, кривая L регулярная. Тем самым условия r(t)ÎCⁿ, n>2, и r'(t₀)≠0 являются условиями локальной регулярности кривой.

ДЛИНА ДУГИ КРИВОЙ