Основные теоремы о пределах. Правила вычисления пределов
В этом разделе будут изложены теоремы, необходимые для вывода правил вычисления пределов. Сначала приведём некоторые определения.
Определение 3.1.Величина 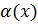 называется бесконечно малой (при
называется бесконечно малой (при 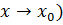 , если
, если 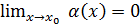 .
.
Определение 3.2.Величина 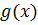 называется бесконечно большой (при
называется бесконечно большой (при 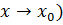 , если
, если 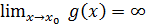 .
.
Определение 3.3.Величина 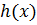 называется ограниченной на интервале
называется ограниченной на интервале 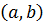 , если
, если 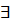 такая константа
такая константа 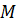 , что
, что 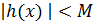 для всех
для всех 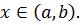
Определение 3.4.Величина 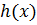 называется ограниченной сверху (снизу) на интервале
называется ограниченной сверху (снизу) на интервале 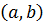 , если
, если 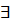 такая константа
такая константа 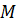 , что
, что 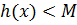 (
( 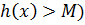 для всех
для всех 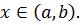
Определение 3.5.Величина 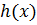 называется ограниченной, ограниченной сверху, ограниченной снизу при
называется ограниченной, ограниченной сверху, ограниченной снизу при 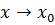 , если существует интервал
, если существует интервал 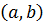 ,
,
-12-
содержащий точку 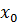 , на котором величина
, на котором величина 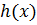 является таковой.
является таковой.
Очевидно, что функции 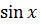 и
и  являются ограниченными на всей числовой оси, так как
являются ограниченными на всей числовой оси, так как 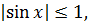
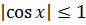 . Функции
. Функции 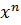 ограниченны на любом интервале
ограниченны на любом интервале 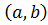 при
при 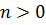 и
и 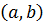 таком, что
таком, что 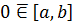 при
при 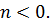
Очевидно, что величина 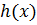 является ограниченной тогда и только тогда, когда она ограниченна и сверху, и снизу.
является ограниченной тогда и только тогда, когда она ограниченна и сверху, и снизу.
Очевидно, что бесконечно малая величина является ограниченной.
Примеры бесконечно малых, бесконечно больших и ограниченных величин будут приведены ниже.
Теорема 3.1.Сумма, разность, произведение бесконечно малых величин являются бесконечно малыми.
Теорема 3.2.Произведение бесконечно малой величины на ограниченную является бесконечно малой.
Теорема 3.3.Если 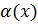 - бесконечно малая, то
- бесконечно малая, то 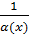 - бесконечно большая.
- бесконечно большая.
Теорема 3.4.Если 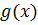 - бесконечно большая, то
- бесконечно большая, то 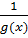 - бесконечно малая.
- бесконечно малая.
Теорема 3.5.Если 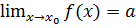 и
и 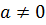 , то
, то 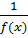 – ограниченная величина.
– ограниченная величина.
Теорема 3.6. 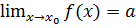 тогда и только тогда, когда
тогда и только тогда, когда 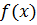 представима в виде
представима в виде 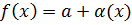 , где .
, где . 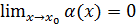 , т.е.
, т.е. 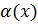 - бесконечно малая.
- бесконечно малая.
Пример 3.1.При 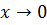 величина
величина 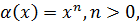 является бесконечно малой, а величина
является бесконечно малой, а величина 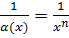 бесконечно большая.
бесконечно большая.
Пример 3.2.Поскольку величина  является ограниченной на всей числовой оси, то при
является ограниченной на всей числовой оси, то при 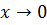 величина
величина 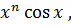
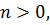 является бесконечно малой.
является бесконечно малой.
Пример 3.3.При 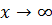 величина
величина 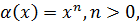 является бесконечно большой, а величины
является бесконечно большой, а величины 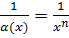 ,
, 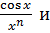
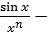 бесконечно малыми.
бесконечно малыми.
Из приведённых выше теорем вытекает следующая теорема о правилах
-13-
вычисления пределов.
Теорема 3.7.Пусть 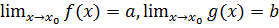 , тогда:
, тогда:
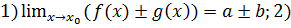
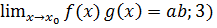 если b
если b 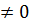 , то
, то 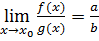 .
.
Замечание 3.1.Поскольку 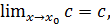 где
где 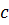 - константа, то из пункта 2) теоремы 3.7 вытекает, что
- константа, то из пункта 2) теоремы 3.7 вытекает, что 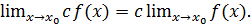
Приведём ещё несколько теорем о пределах для полноты изложения.
Теорема 3.7 ( о сжатой переменной).Если 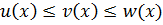 и
и 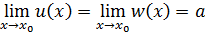 , то
, то 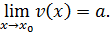
Теорема 3.8.Если 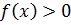 (
( 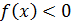 ) и
) и 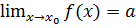 , то
, то 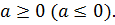
Теорема 3.9.Если 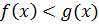 и
и 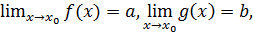 то
то 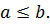
Определение 3.6.Функция 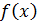 называется монотонно возрастающей на интервале
называется монотонно возрастающей на интервале 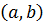 , если из того, что
, если из того, что 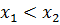 ,
, 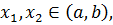 следует, что
следует, что 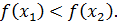
Теорема 3.10.Если функция 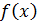 является монотонно возрастающей и ограниченной сверху, т.е.
является монотонно возрастающей и ограниченной сверху, т.е. 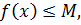 (снизу, т.е.
(снизу, т.е. 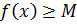 ) на интервале
) на интервале 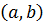 , то существует конечный предел
, то существует конечный предел 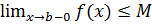 (
( 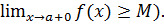
Замечание 3.2.В теореме 3.10 границы интервала 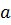 и
и 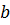 могут быть равными также
могут быть равными также 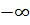 и
и 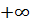 соответственно.
соответственно.
Непрерывные функции.
Определение 4.1.Функция 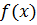 называется непрерывной в точке
называется непрерывной в точке 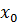 , если
, если 
Определение 4.2.Функция 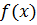 называется непрерывной слева (справа) в точке
называется непрерывной слева (справа) в точке 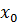 , если
, если 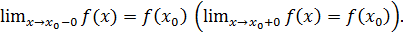
Определение 4.3.Функция 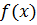 называется непрерывной на интервале
называется непрерывной на интервале 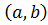 , если она непрерывна в каждой точке этого интервала. -14-
, если она непрерывна в каждой точке этого интервала. -14-
Определение 4.4.Функция 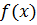 называется непрерывной на интервале
называется непрерывной на интервале 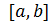 , если она непрерывна на интервале
, если она непрерывна на интервале 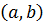 , непрерывна справа в точке
, непрерывна справа в точке 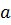 и непрерывна слева в точке
и непрерывна слева в точке 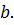
Определение 4.5.Если функция 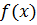 не является непрерывной в точк
не является непрерывной в точк 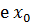 , то она называется разрывной в этой точке.
, то она называется разрывной в этой точке.
Пример 4.1.Функция 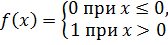 непрерывна всюду, кроме точки
непрерывна всюду, кроме точки 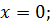 в точке
в точке 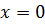 она является непрерывной слева.
она является непрерывной слева.
Теорема 4.1.Всякая элементарная функция непрерывна в каждой точке своей области определения.
Теорема 4.2.Пусть 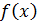 и
и 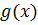 непрерывны. Тогда
непрерывны. Тогда 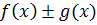 ,
, 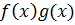 непрерывны;
непрерывны; 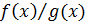 непрерывна, если
непрерывна, если 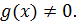
Теорема 4.3.Если функция 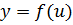 непрерывна в точке
непрерывна в точке 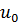 , а функция
, а функция 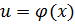 непрерывна в точке
непрерывна в точке 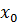 , причём
, причём 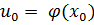 , то функция
, то функция 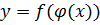 непрерывна в точке
непрерывна в точке 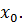
Т.е. сложная функция непрерывных функций является непрерывной функцией.
Геометрически непрерывность функции означает, что её график является сплошной, неразрывной линией.
