Понятие предела функции в точке. Теоремы о пределах. Виды пределов

Ответ:

Предел функции в заданной точке — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.

теоремы:

Если значения функций в окрестности некоторой точки равны, то и их пределы в этой точке совпадают

Если функция имеет предел, то он единственный.

Предел константы равен этой константе

Непрерывность функции в точке и на промежутке. Точки разрыва функции

Ответ:

Функция называется непрерывной в точке, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
функция имеет точку разрыва первого рода при, если в это точке существуют левосторонний предел и правосторонний предел, эти односторонние пределы конечны.
Функция имеет точку разрыва второго рода при, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Раскрытие неопределенностей

Ответ:

Неопределенность типа 𝟎𝟎

Пусть заданы две функции f(x) и g(x) , такие, что

𝐥𝐢𝐦𝒙→𝒂𝐟(𝐱)=𝟎 и 𝐥𝐢𝐦𝒙→𝒂𝐠(𝐱)=𝟎

В этом случае говорят, что функция 𝒇(𝒙)𝒈(𝒙) имеет неопределённость 𝟎𝟎 в точке x=a. Чтобы найти предел при х=а, когда функция 𝒇(𝒙)𝒈(𝒙) содержит неопределённость 𝟎𝟎, нужно разложить на множители численность и/или знаменатель и затем сократить члены, стремящиеся к нулю. Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя.

Неопределенность типа ∞∞

Пусть две функции f(x) и g(x) обладают свойством

𝐥𝐢𝐦𝒙→𝒂𝐟(𝐱)=±∞ и 𝐥𝐢𝐦𝒙→𝒂𝐠(𝐱)=±∞

Где a является действительным числом, либо стремится к + или -∞. В Этом случае функция имеет в точке а неопределённость типа ∞∞. Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.

Неопределенности типа ∞−∞, 0*∞, ∞^0, 1^∞

Неопределённости этих типов сводятся к рассмотренным выше неопределённостям типа 𝟎𝟎 и ∞∞.

5.

6.Асимптоты графика функции

Ответ:

Асимптота – это прямая, к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.

1) Вертикальные асимптоты, которые задаются уравнением вида 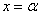, где «альфа» – действительное число. Популярная представительница 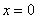определяет саму ось ординат, вспоминаем гиперболу .

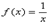Таким образом, чтобы установить наличие вертикальной асимптоты 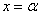в точке x=0 достаточно показать, что хотя бы один из односторонних пределов 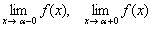бесконечен. Чаще всего это точка, где знаменатель функции равен нулю.

2)Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом 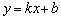. Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты 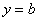. Например, та же гипербола с асимптотой 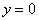.Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше двух наклонных асимптот. 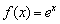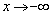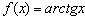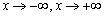Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при , а график арктангенса при – двумя такими асимптотами, причём различными. Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью 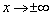. Например,: .

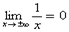Общее практическое правило:Если существуют два конечных предела 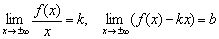, то прямая 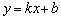является наклонной асимптотой графика функци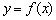и при 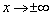. Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.

3) Горизонтальные асимптоты

Если существует конечный предел 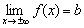, то прямая 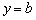является горизонтальной асимптотой графика функци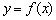и при .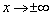

Нетрудно заметить, что числитель и знаменатель функции 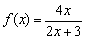одного порядка роста, а значит, искомый предел будет конечным:

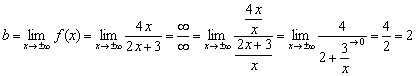
Поведение на бесконечности

Исследуем поведение функции на бесконечности, то есть при .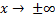

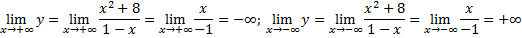
7.

8.

9.

10.

11.

12.

13.

14.Возрастание и убывание функций.

Ответ:

Определение возрастающей функции: Функция 𝑓(𝑥) называется возрастающей на некотором интервале, если для любых двух точек 𝑥1 и 𝑥2 этого интервала, таких что 𝑥1<𝑥2, справедливо 𝑓(𝑥1)<𝑓(𝑥2). Другими словами, большему значению аргумента соответствует большее значение функции.

Определение убывающей функции: Функция 𝑓(𝑥) называется убывающей на некотором интервале, если для любых двух точек 𝑥1 и 𝑥2 этого интервала, таких что 𝑥1<𝑥2, справедливо 𝑓(𝑥1)>𝑓(𝑥2). Другими словами, большему значению аргумента соответствует меньшее значение функции.