Уравнения прямой и плоскости в пространстве

Расстояние между двумя точками 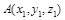и :

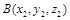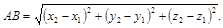(14)

Деление отрезка 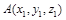, 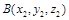точкой 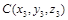в заданном отношении :

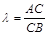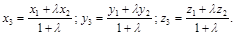(15)

Уравнение прямой, которая проходит через точку 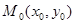в заданном направлении:

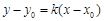, (16)

где k – ее угловой коэффициент.

Если прямая параллельна оси 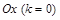, то ее уравнение 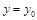, если прямая параллельная оси 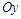, то ее уравнение .

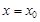Уравнение прямой, которая проходит через две точки 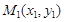и :

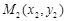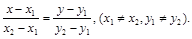(17)

Пересечение двух прямых находится по формуле:

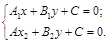(18)

Система имеет единое решение, если .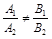

Если 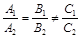, то прямые параллельны. (19)

Если 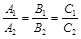, то прямые совпадают. . (20)

Каноническое уравнение прямой в пространстве:

,

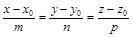где 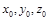– координаты точки, через которую проходит прямая, а m, n, p – направляющие коэффициенты прямой, которые являются проекциями на координатные оси Ox, Oy, Oz направляющего вектора прямой.

Острый угол между прямой 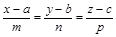и плоскостью :

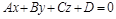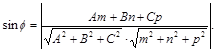(21)

Уравнение прямой, которая проходит через две данные точкиА (х₁, b₁, z₁) и B (x₂, y₂, x₂):

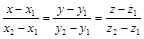. (22)

Условие параллельности прямой и плоскости:

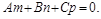(23)

Условие перпендикулярности прямой и плоскости:

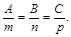(24)

Общее уравнение плоскости:

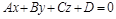. (25)

Вектор 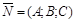, перпендикулярный плоскости, называется нормальным вектором плоскости.

Уравнение плоскости, которая проходит через точку 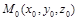перпендикулярно вектору :

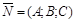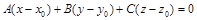. (26)

Уравнение плоскости, проходящей через три точки , , :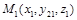

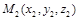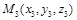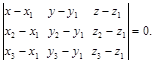(27)

Уравнение плоскости в отрезках на осях:

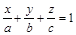, (28)

где a, b, и с – величины отрезков, которые отсекает плоскость на осях координат.

Уравнение связки плоскостей, проходящих через точку :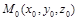

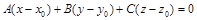. (29)

Коэффициенты А, В, С определяют разные плоскости, которые проходят через данную точку.

Угол 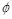между плоскостям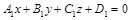и и :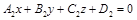

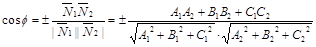. (30)

Условие параллельности плоскостей:

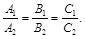(31)

Условие перпендикулярности плоскостей:

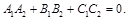(32)

Расстояние от точки 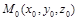до плоскости :

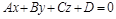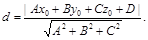(33)

Пример 1. Составить уравнение прямой, которая проходит через точки А (3; – 4) и В (4; 5).

Решение. За первую примем, например, точку А, тогда, х₁ = 3, х₂ = 4, b₁ = – 4, b₂ = 5.

Имеем

.

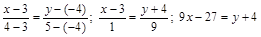Общее уравнение прямой

.

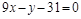Пример 2.Составить уравнение прямой, которая проходит через точку А(3; –4) параллельно прямой 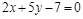, и перпендикулярно ей.

Решение. Угловой коэффициент данной прямой 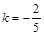. Соответственно условиям параллельности и перпендикулярности двух прямых угловой коэффициент параллельной прямой 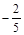, а перпендикулярной прямой 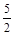, тогда уравнения искомых прямых имеют вид:

параллельной –

,

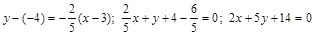перпендикулярной –

.

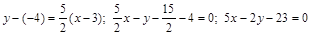Пример 2.Определить расстояние от точки 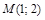до прямой .

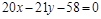Решение. Имеем

.

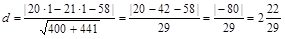Пример 3. Найти расстояние от точки 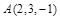до плоскости .

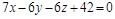Решение. Подставив в формулу расстояния от точки до плоскости значения А = 7; В = – 6; Z = – 6; х₁ = 2; b₁ = 3; z₁ = –1, имеем:

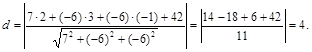
Пример 4. Уравнение плоскости 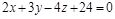преобразовать в формулу отрезков на осях.

Решение. Перенесем свободный член 24 в правую часть уравнения и получим .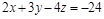

Разделив обе части на – 24, получим:

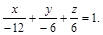
Пример 3. Найти острый угол между плоскостями:

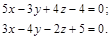
Решение. По формуле угла между плоскостями получим, если учесть, что

А₁= 5; В₁ = – 3; Z₁ = 4; и А₂ =3; В₂ = – 4; Z₂ = –2:

; ; ; .

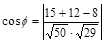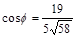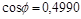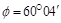В формуле следует взять абсолютную величину правой части, так как надо найти острый угол между плоскостями и, значит, .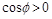

Пример 6.Вычислить объем тетраэдра с вершинам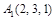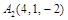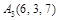и , , и 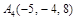, и его высоту, опущенную из вершины 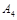на грань .

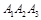Решение. Из вершины 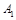проведем векторы 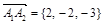, 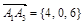и .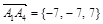

В соответствии с геометрическим смыслом смешанного произведения

.

С другой стороны,

,

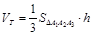где соответственно геометрическому смыслу векторного произведения

.

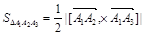Тогда

.

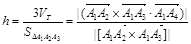Вычисляем смешанное произведение:

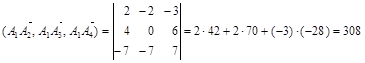
и находим объем тетраэдра

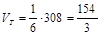(ед. длины)³.

Вычисляем координаты векторного произведения:

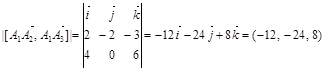
и его модуль

.

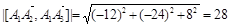Находим высоту:

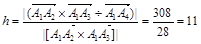(ед. длины).

Итак, 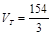(ед. длины)³, 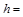11 (ед. длины).