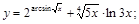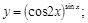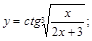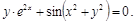Производные и дифференциалы высших порядков
Определение 1. Производной второго порядка (второй производной функции) 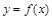 в точке х называется производная от ее первой производной
в точке х называется производная от ее первой производной 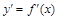 при условии, что
при условии, что 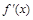 дифференцируема в точке х. Она обозначается такими символами:
дифференцируема в точке х. Она обозначается такими символами:
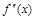 ,
, 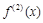 ,
, 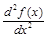 ,
, 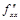 ,
, 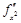 .
.
Определение 2. Производной п-го порядка функции 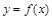 называется производная от производной (п-1) порядка:
называется производная от производной (п-1) порядка:
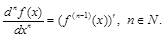
Определение 3.Производную, для которой существует п-я производная в точке х, называют п раз дифференцируемой в этой точке.
Основные формулы вычисления производных высших порядков
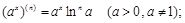 (1)
(1)
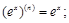 (2)
(2)
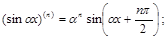 (3)
(3)
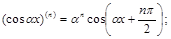 (4)
(4)
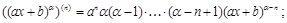 (5)
(5)
в частности,
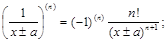 (6)
(6)
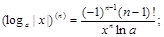 (7)
(7)
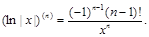 (8)
(8)
Основные правила вычисления производных
Если функции 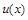 и
и 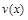 п раз дифференцированы, тогда имеют место такие равенства:
п раз дифференцированы, тогда имеют место такие равенства:
1) 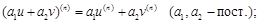 (9)
(9)
2) 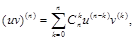 (формула Лейбница)(10)
(формула Лейбница)(10)
где 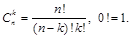
Вычисление производных высших порядков функций,
Заданных параметрически
Если функция задана параметрически уравнениями 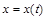 ,
, 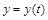 , тогда производные
, тогда производные 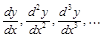 вычисляются по формулам:
вычисляются по формулам:
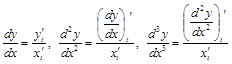 и т.д. (11)
и т.д. (11)
Для производной второго порядка имеет место формула:
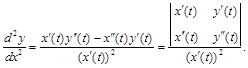 (12)
(12)
Дифференциалы высших порядков
Определение 4. Дифференциалом второго порядка дважды дифференцируемой функции 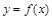 называют дифференциал от дифференциала первого порядка функции
называют дифференциал от дифференциала первого порядка функции 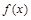 , т.е.
, т.е. 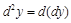 .
.
В случае, когда х – независимая переменная, дифференциалы вычисляются по формулам:
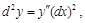
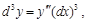
………………......
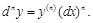 (13)
(13)
Если же х — некоторая функция от t, 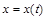 , тогда
, тогда
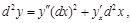 (14)
(14)
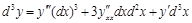 и т.д. (15)
и т.д. (15)
Если для функций 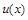 и
и 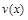 , где х – независимая перемен-ная, существуют дифференциалы
, где х – независимая перемен-ная, существуют дифференциалы 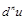 и
и 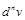 , тогда
, тогда
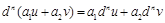 (
( 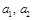 — постоянные), (16)
— постоянные), (16)
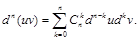 (17)
(17)
Пример 1. Найти производную второго порядка функции, заданной параметрически 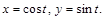
Решение.
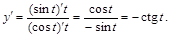
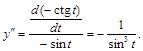
Пример 2. Найти производную второго порядка функции
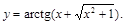
Решение.Сначала находится первая производная от сложной функции:
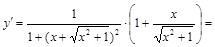
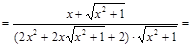
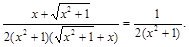
Тогда вторая производная равняется:
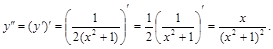
Пример 3. Найти дифференциал второго порядка функции 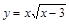 в точке
в точке 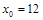 .
.
Решение.Согласно формуле для вычисления дифференциала второго порядка 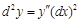 вычисляется
вычисляется 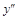 :
:
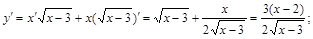
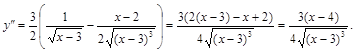
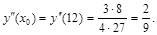
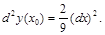
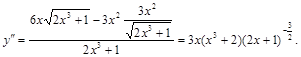
Упражнения к разделу 3.2
Найти производные функций:
1). 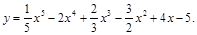
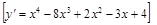
2). 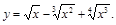
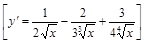
3). 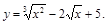
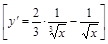
4). 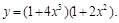
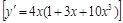
5). 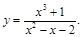
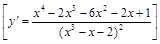
6). 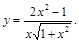
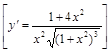
Найти производные сложных функций:
7). 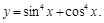
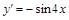
8). 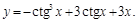
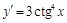
9). 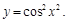
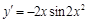
10). 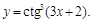
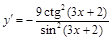
Найти производную функций:
11). 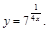
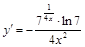
12). 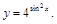
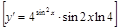
13). 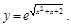
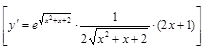
14). 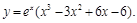
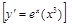
15). 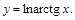
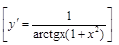
Найти производные функций, которые заданы неявно:
16). 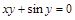 .
. 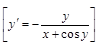
17). 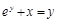 .
. 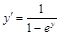
18). 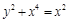 .
. 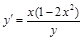
Найти производную функции, которая задана параметрически:
19). 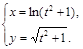
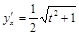
20). 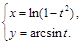
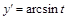
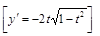
21). 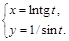
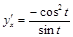
Найти производные функций, логарифмируя их:
22). 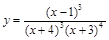 .
. 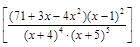
23). 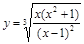 .
. 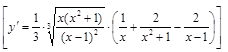
24). 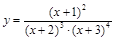 .
. 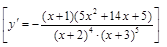
Найти уравнение касательной и нормали к графику функции 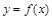 в точке
в точке 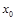 .
.
25). 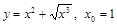 .
. 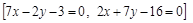
26). 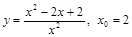 .
. 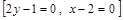
Найти точки, в которых касательные к графику функции 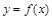 параллельны оси абсцисс:
параллельны оси абсцисс:
27). 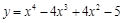 .
. 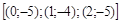
Написать уравнение касательной и нормали к кривой
28) 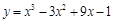 в точке
в точке 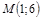 .
.
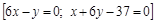
Найти производные второго порядка функций:
29). 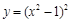 .
. 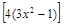
30). 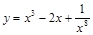 .
. 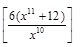
31). 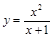 .
. 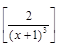
Вычислить производные функций, заданных неявно:
32). 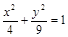 .
. 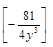
33). 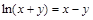 .
. 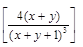
Задания для индивидуальной семестровой работы студентов к разделу 3.2
Найти производные функций:
1). 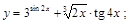
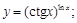
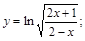
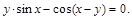
2). 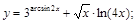
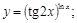
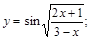
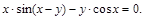
3). 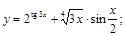
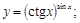
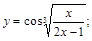
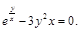
4). 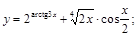
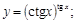
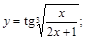
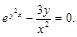
5). 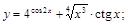
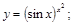
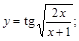
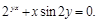
6). 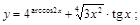
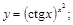
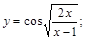
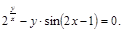
7). 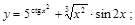
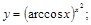
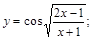
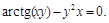
8). 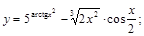
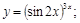
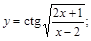
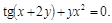
9). 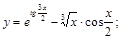
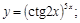
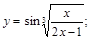
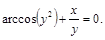
10). 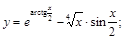
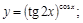
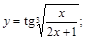
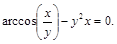
11). 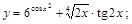
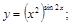
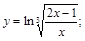
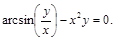
12). 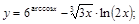
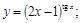
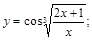
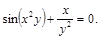
13). 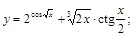
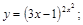
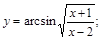
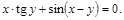
14). 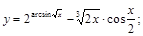
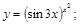
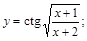
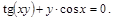
15). 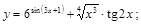
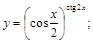
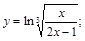
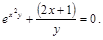
16). 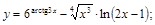
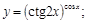
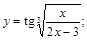
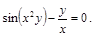
17). 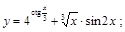
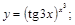
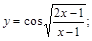
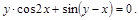
18). 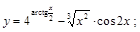
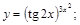
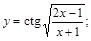
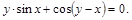
19). 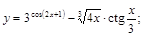
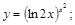
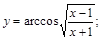
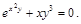
20). 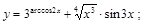
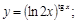
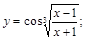
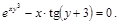
21). 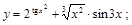
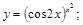
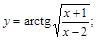
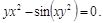
22). 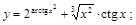
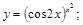
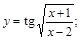
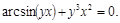
23). 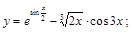
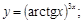

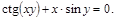
24). 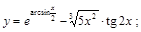
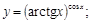
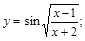
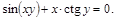
25). 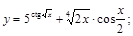
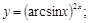
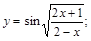
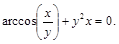
26). 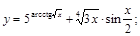
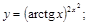
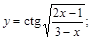
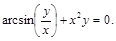
27). 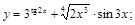
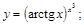
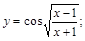
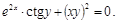
28). 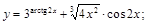
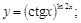
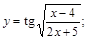
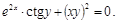
29). 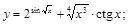
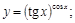
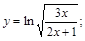
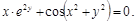
30).