Предел последовательности
Последовательность 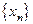 называется сходящейся, если существует вещественное число
называется сходящейся, если существует вещественное число 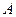 такое, что для любого
такое, что для любого 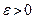 найдется число
найдется число 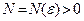 (возможно не целое и зависящее от
(возможно не целое и зависящее от 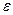 ), что при выполнении условия
), что при выполнении условия 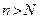 имеет место неравенство
имеет место неравенство 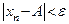 . При этом число
. При этом число 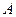 называется пределом последовательностии обозначается
называется пределом последовательностии обозначается
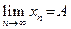 .
.
Определение предела последовательности с помощью кванторов можно записать так:
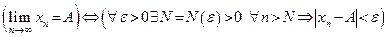 .
.
Геометрическая иллюстрация приведена на рис. 1. Если число 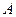 является пределом последовательности
является пределом последовательности 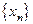 , то для любого числа
, то для любого числа 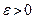 вне промежутка
вне промежутка 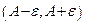 содержится лишь конечное количество членов последовательности
содержится лишь конечное количество членов последовательности 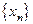 . На рис. 1 членам последовательности соответствуют точки, а промежутке
. На рис. 1 членам последовательности соответствуют точки, а промежутке 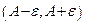 – светлая полоса.
– светлая полоса.
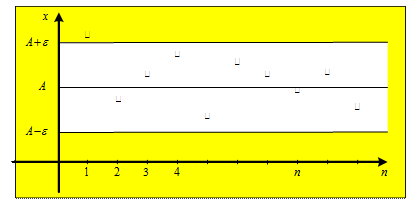
Рис. 1
Непосредственно из определения сходящейся последовательности, следует следующее утверждение.
Теорема 4.1. Всякая сходящаяся последовательность является ограниченной.
Замечание 4.1. Из ограниченности последовательности не следует ее сходимость. Например, последовательность
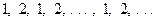 (4.1)
(4.1)
является ограниченной, но она не является сходящейся. Однако справедливо следующее утверждение.
Теорема 4.2 (Больцано-Вейерштрасса). Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Для последовательности (4.1) любая подпоследовательность, у которой начиная с некоторого номера все члены равны 1 (или равны 2), является примером сходящейся подпоследовательности.
Бесконечно малая величина
В теории числовых последовательностей важную роль играет бесконечно малая величина.
Последовательность 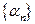 называется бесконечно малой величиной, если она сходящаяся и её предел равен нулю:
называется бесконечно малой величиной, если она сходящаяся и её предел равен нулю:
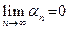 .
.
Пример 5.1. Последовательность 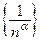 , где
, где 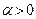 – произвольное число, является бесконечно малой величиной:
– произвольное число, является бесконечно малой величиной:
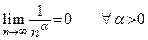 .
.
Пример 5.2. Последовательность 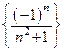 –бесконечно малая величина:
–бесконечно малая величина:
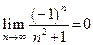 .
.
Отметим два важных свойств бесконечно малых величин.
Свойство 5.1. Сумма двух бесконечно малых величин является бесконечно малой величиной.
Следствие 5.1. Сумма любого конечного числа бесконечно малых величин является бесконечно малой величиной.
Свойство 5.2. Произведение бесконечно малой величины на ограниченную величину является бесконечно малой величиной.
Связь между сходящейся последовательности, её пределом и бесконечно малой величины приводится в следующей теореме.
Теорема 5.1. Для того, что последовательность 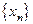 являлась сходящейся с пределом равным
являлась сходящейся с пределом равным 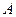 , необходимо и достаточно, чтобы имело место представление
, необходимо и достаточно, чтобы имело место представление
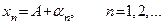 ,
,
где 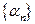 – некоторая бесконечно малая величина.
– некоторая бесконечно малая величина.
