Логарифмическое дифференцирование

Практикум

По математическому анализу

Для студентов вечернего отделения

Го курса

(Часть II)

Учебно-методическое пособие

Москва, 2006 г.

УДК 512.8:516

ББК С42

Рецензенты: к.ф.-м.н., доцент Каролинская С.Н. (МАИ им. С.Орджоникидзе); к.ф.-м.н., доцент Краснослободцева Т.П. (МИТХТ им. М.В. Ломоносова).

Скворцова М.И., Мудракова О.А., Кротов Г.С. Практикум по математическому анализу для студентов вечернего отделения 1-го курса (Часть II). Учебно-методическое пособие — М.: МИТХТ, 2006 г, 32 стр., рис. 3.

Пособие представляет собой конспекты шести практических занятий по курсу математического анализа для студентов вечернего отделения МИТХТ им. М. В. Ломоносова. Оно является продолжением части I одноименного учебно-методического пособия тех же авторов. В часть II включены следующие разделы: «Производная функции одной переменной», «Исследование функций и построение их графиков».

Каждое занятие посвящено отдельной теме. Конспекты пяти занятий содержат краткое изложение соответствующей теории, типовые примеры и задачи для самостоятельного решения (с ответами). В конспекте занятия №10 приведен образец варианта контрольной работы (с решениями), проводимой на этом занятии. Дан перечень 40 вариантов домашней контрольной работы по теме «Исследование функций и построение их графиков».

Пособие предназначено для студентов вечернего отделения вузов химического профиля.

© МИТХТ им. М.В. Ломоносова, 2006 г.

Оглавление

Занятие 7. Производная функции одной переменной. Производная сложной функции. Логарифмическое дифференцирование……………..4

Занятие 8. Уравнения касательной и нормали к кривой. Угол между кривыми. Дифференциал функции. Приближённое вычисление значения функции в точке ..………….………………………………………………..8

Занятие 9.Правило Лопиталя для вычисления пределов. Производная функции, заданной параметрически...…….………………………………12

Занятие 10.Контрольная работа №2 по теме "Производная функции одной переменной». Вариант-образец……………………………………16

Занятие 11.Исследование функций (нахождение интервалов возрастания (убывания) функций, экстремумов, интервалов выпуклости (вогнутости), точек перегиба, асимптот графика функции)….………..18

Занятие 12.Общая схема исследования функций и построения их графиков……………………..…………………….……….………...........23

Перечень вариантов домашней контрольной работы по теме «Исследование функций и построение их графиков»………………….29

Литература…………………………………………….……………........32

Занятие 7.

Производная функции одной переменной.

Производная сложной функции.

Логарифмическое дифференцирование.

Определение. Приращением функции 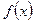в точке 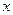называется следующая разность:

,

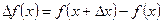где 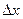— приращение аргумента в точке .

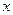Определение. Производной 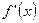функции 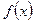в точке 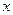называется следующий предел:

.

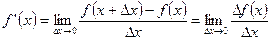Свойства производной

1) 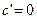( 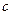— константа);

2) 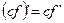( 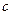— константа);

3) ;

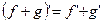4) ;

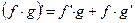5) ;

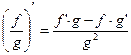Таблица производных

основных элементарных функций

1) ;

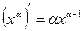2) ; ;

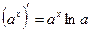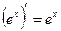3) ; ;

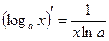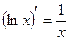4) ;

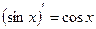5) ;

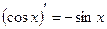6) ;

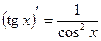7) ;

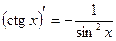8) ;

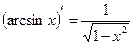9) ;

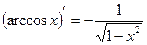10) ;

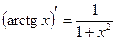11) .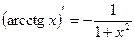