II. Элементы математического анализа
I. Элементы линейной алгебры
1.Решить матричное уравнение: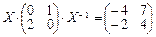 
Ответ: 1.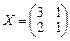 
2. 
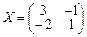
3. 
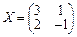
2.Найти определитель матрицы: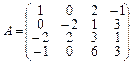 
Ответ:1.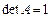 
2. 
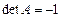
3. 
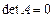
3.Найти наибольшее значение определителей 3-го порядка составленных из чисел 0 и 1.
Ответ:1. наибольшее значение равно 1
2. наибольшее значение равно 2
3. наибольшее значение равно 3
4.Какой из следующих векторов является собственным для матрицы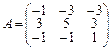 
Ответ:1.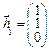 
2. 
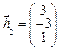
3. 
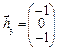
5.При каком из приведенных значений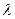 
квадратичная форма 
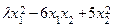является положительно определённой?
Ответ:1.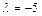 
2. 
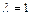
3. 
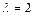
6.При каком из приведенных значений 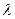последовательность векторов 
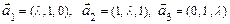является базисом 3-х мерного пространства 
?
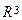Ответ:1.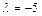
2. 
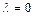
3. 
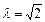
7.Выяснить, в каком из указанных ниже случаев функция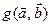 
, определённая для любых векторов 
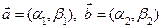, может служить скалярным умножением в пространстве 
.
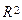Ответ:1.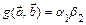 
2. 
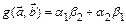
3. 
.
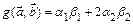8.Выяснить, какая из указанных ниже последовательностей векторов является ортонормированным базисом подпространства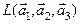 
, порождённого векторами 
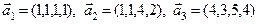некоторого четырёхмерного евклидова пространства V. Считаем, что координаты векторов заданы в некотором ортонормированном базисе пространства V.
Ответ:1.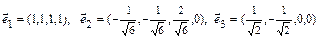 
2. 
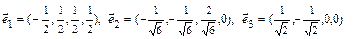
3. 
.
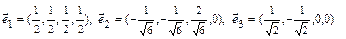II. Элементы математического анализа
9.Для функции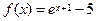 
найти область определения её обратной функции ( 
).
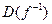Ответ:1.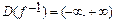 
2. 
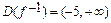
3. 
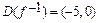
10.Вычислить предел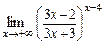 
.
Ответ:1.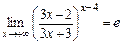 
2. 
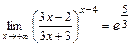
3. 
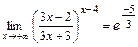
11.Определить характер разрыва функции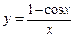 
в точке 
.
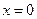Ответ:1.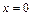 
– точка устранимого разрыва
2. в точке 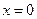– разрыв типа «скачок»
3. в точке 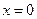– разрыв 2-го рода
12.Определить, какое из приведённых ниже уравнений является уравнением наклонной асимптоты к графику функции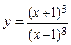 
?
Ответ:1.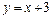 
2. 
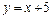
3. 
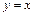
13.Определить, на каком из указанных ниже интервалов функция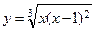 
является монотонной?
Ответ:1.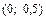 
2. 
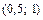
3. 
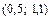
14.Определить число точек перегиба функции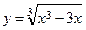 
.
Ответ:1. одна точка перегиба
2. две точка перегиба
3. три точка перегиба
15.Вычислить неопределённый интеграл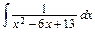 
Ответ:1.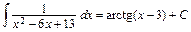 
2. 
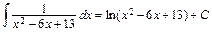
3. 
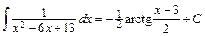
16.Определить коэффициент перед слагаемым, содержащим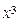 
в разложении функции 
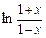в ряд по степеням x (разложение в ряд Маклорена).
Ответ:1. коэффициент перед 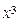равен 
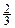
2. коэффициент перед 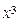равен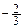 
3. коэффициент перед 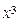равен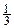 
17.Для функции двух переменных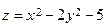 
найти градиент в точке 
( 
).
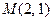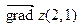Ответ:1.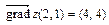 
2. 
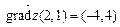
3. 
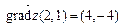
18.Для функции двух переменных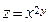 
найти смешанную частную производную 
.
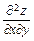Ответ:1.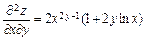 
2. 
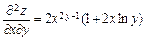
3. 
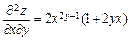
III. Некоторые вопросы оптимизации
19.Определить наибольшее значение функции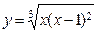 
на интервале 
.
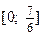Ответ:1.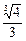 
2. 
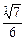
3. 
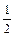
20.Определить, какая из указанных ниже точек является точкой локального минимума функции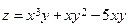 
?
Ответ:1.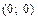 
2. 
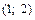
3. 
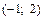
21.Определить, для какой из приведённых ниже функций точка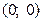 
не является точкой экстремума?
Ответ:1.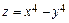 
2. 
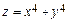
3. 
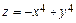
22.Дана функция трёх переменных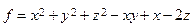 
и точка 
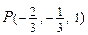. Определить, какому из перечисленных ниже условий удовлетворяет точка Р?
Ответ:1. Р – точка максимума
2. Р – точка минимума
3. Р – не является точкой экстремума
23.Найти, если они есть, точки экстремума функции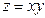 
при условии, что точки 
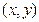лежат на прямой 
.
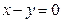Ответ:1. точек экстремума нет.
2. 
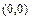– точка экстремума
3. 
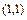– точка экстремума
24.Найти минимум функции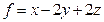 
на сфере 
.
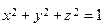Ответ:1.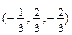 
2. 
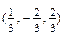
3. 
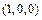
25.Найти наибольшее значение функции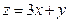 
в области плоскости, которая задаётся условием: 
.
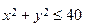Ответ:1. 22
2. 18
3. 20