Элементы математического анализа
Пределы и непрерывность
Отметим некоторые теоремы о пределах, которые часто применяются для решения задач.
Если существуют конечные пределы 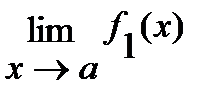 и
и 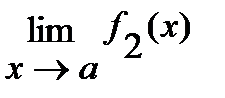 , то
, то
1) 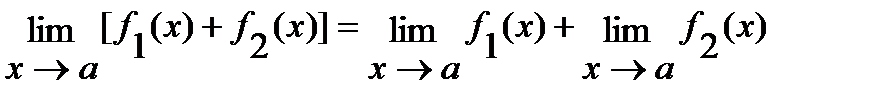 ;
;
2) 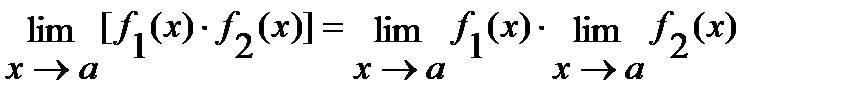 ;
;
3) 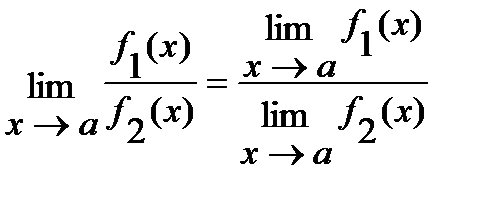 ( если
( если 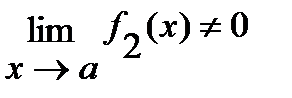 ).
).
Отметим еще два замечательных предела и следствия из них:
1) 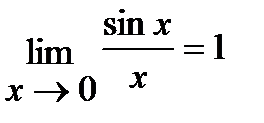 ;
;
2) 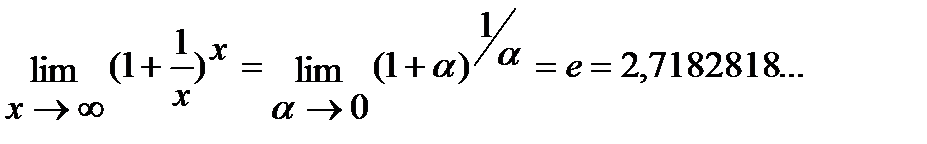 ;
;
3) 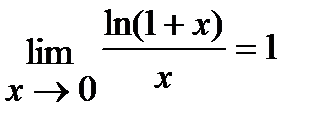 ; 4)
; 4) 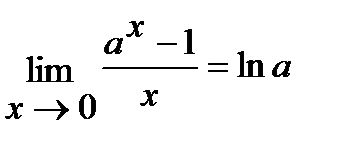 ; 5)
; 5) 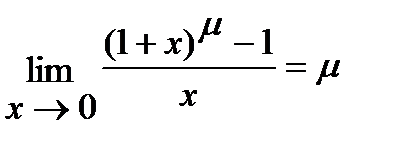 .
.
Задача. Найти указанные пределы, не пользуясь правилом Лопиталя:
а) 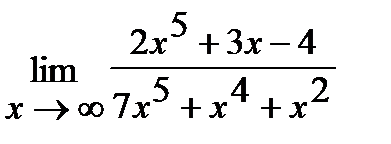 ;
;
б) 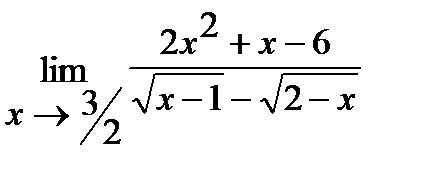 ;
;
в) 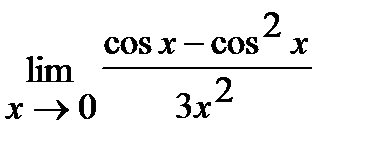 ;
;
г) 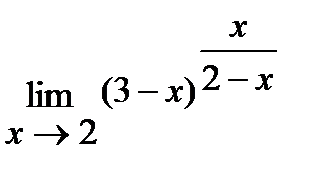 ;
;
д) 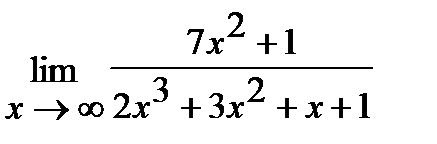 ;
;
е) 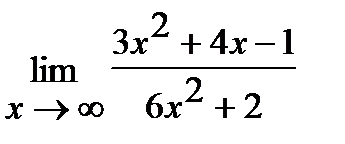 . ж)
. ж) 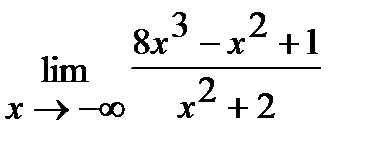 .
.
Решение. а) Если 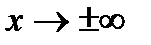 , то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на
, то для нахождения предела частного двух многочленов достаточно разделить и числитель, и знаменатель дроби, стоящей под знаком предела, на 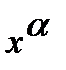 , где
, где 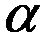 - степень многочлена, стоящего в знаменателе:
- степень многочлена, стоящего в знаменателе: 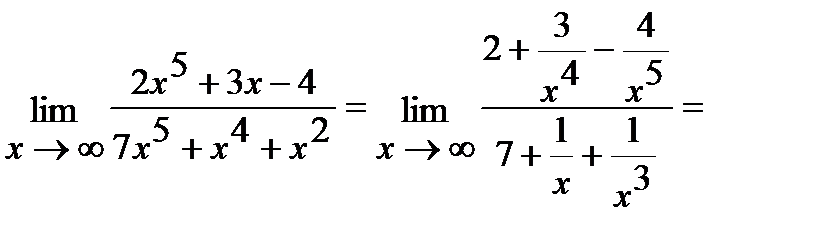
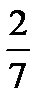 .
.
б) Умножим числитель и знаменатель дроби на 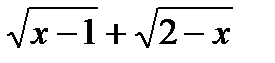 , избавившись тем самым от иррациональности в знаменателе. Итак,
, избавившись тем самым от иррациональности в знаменателе. Итак,
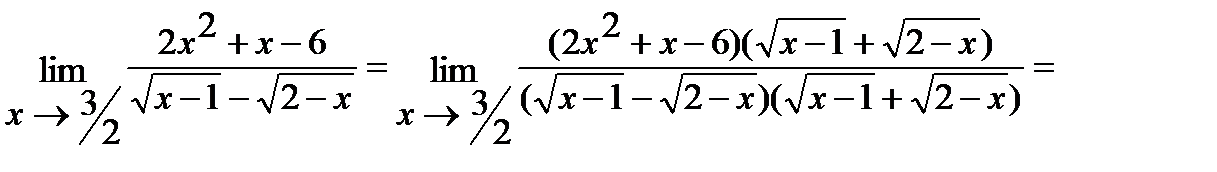
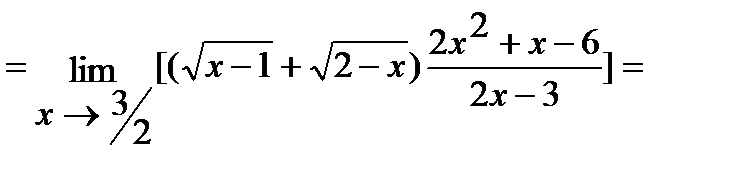
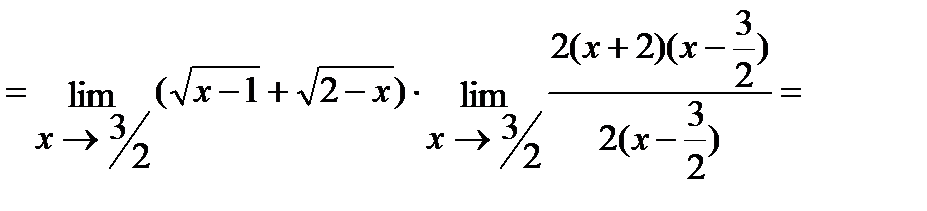
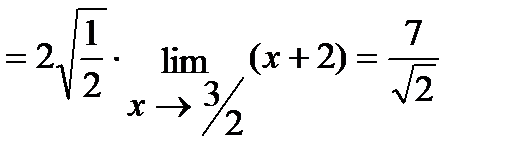 .
.
в) Для решения этой задачи воспользуемся первым замечательным пределом:
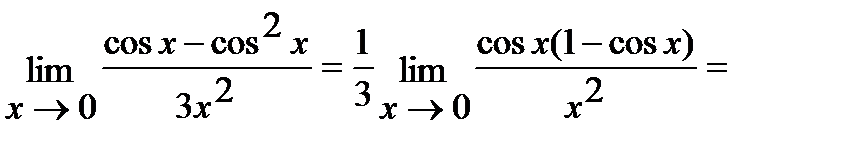
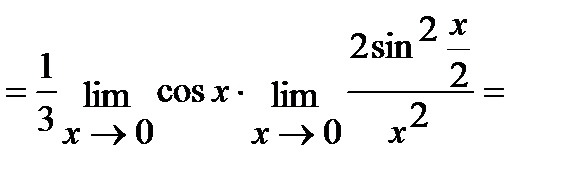
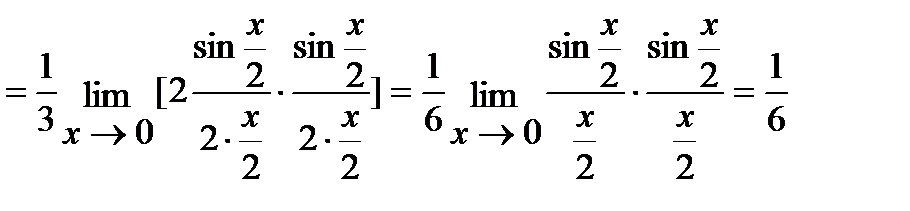
(Так как 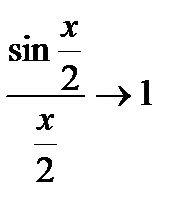 при
при 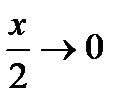 ).
).
г) Для решения данной задачи воспользуемся вторым замечательным пределом:
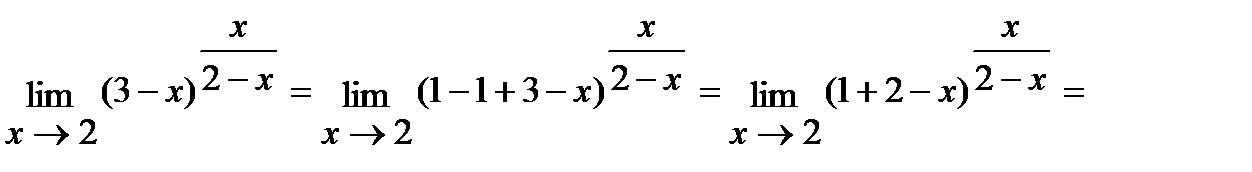
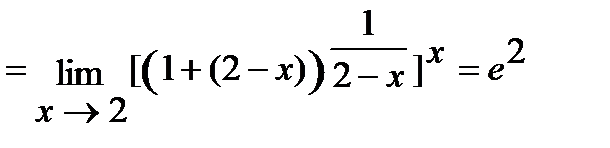 .
.
Последнее равенство вытекает из того, что в квадратной скобке стоит 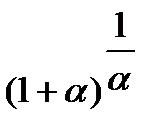 , где
, где 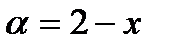 .
.
Решения задач е, ж аналогичны решению задачи а.
Например, задача ж имеет следующее решение:
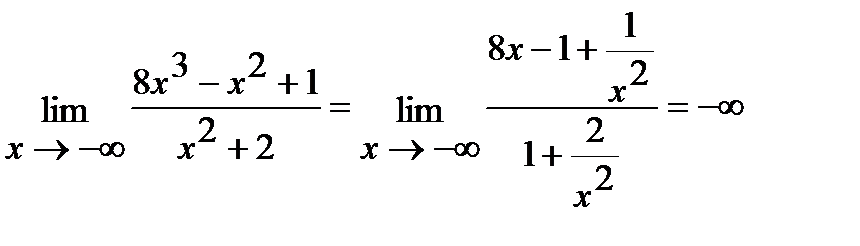 .
.
Производная функции
Производная функция 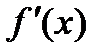 от функции
от функции 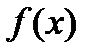 в данной точке
в данной точке 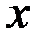 определяется равенством
определяется равенством
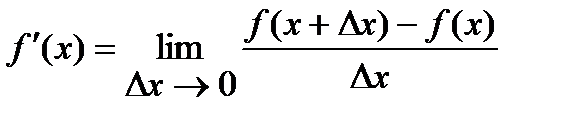 .
.
Таблица производных выглядит следующим образом:
1. 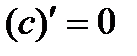 . 2.
. 2. 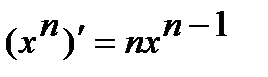 .
.
3. 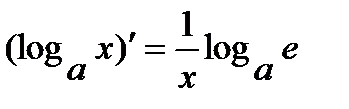 , в частности
, в частности 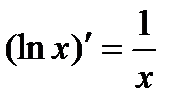 .
.
4. 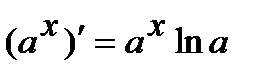 , в частности
, в частности 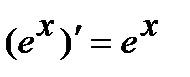 .
.
5. 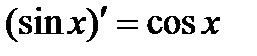 . 9.
. 9. 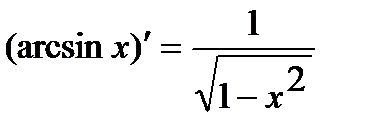 .
.
6. 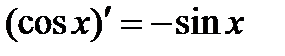 . 10.
. 10. 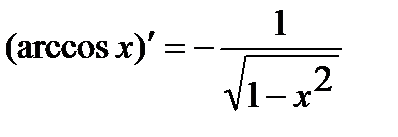 .
.
7. 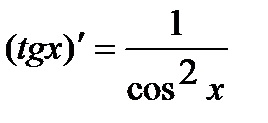 . 11.
. 11. 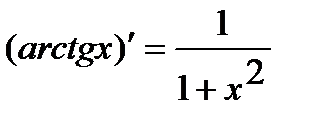 .
.
8. 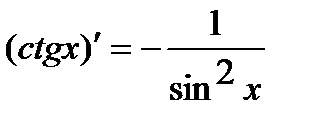 . 12.
. 12. 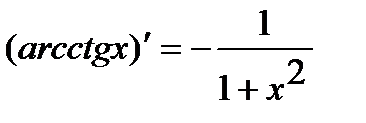 .
.
Основные правила дифференцирования
1. 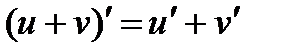 2.
2. 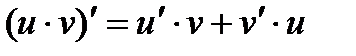 ,в частности,
,в частности,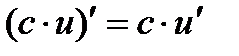 3.
3. 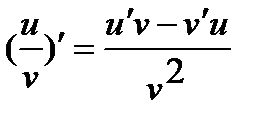 ,где
,где 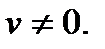
Задача. Найти производные следующих функций:
а) 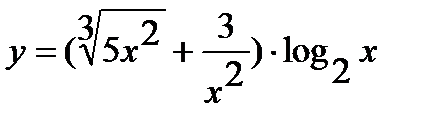 ; б)
; б) 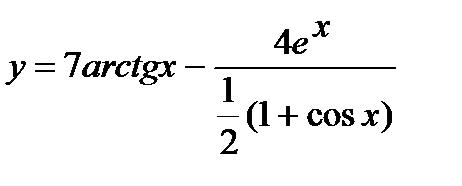 .
.
Решение. а) Преобразуем выражение в скобках, переходя к дробным и отрицательным показателям. Получим
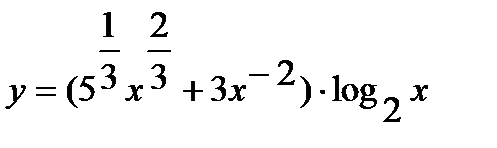 .
.
Используя правило дифференцирования произведения и суммы находим 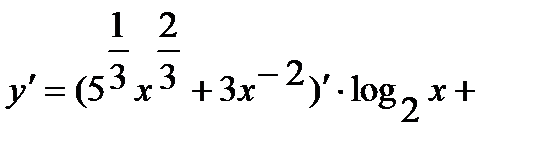
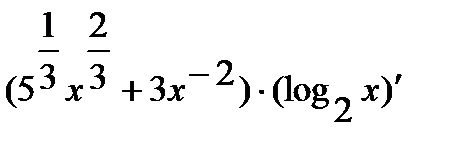 =
=
= 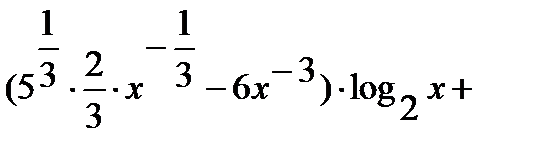
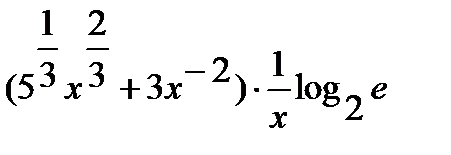 .
.
б) Проведем предварительное преобразование функции:
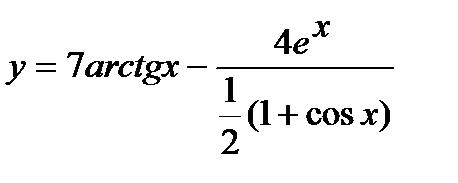 =
= 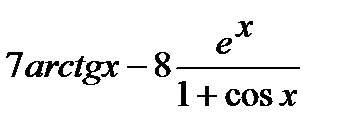 .
.
Используя правила дифференцирования произведения, суммы и частного, получим
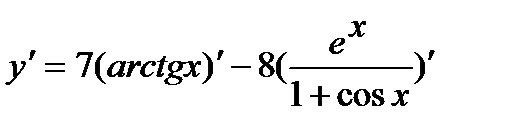 =
=
= 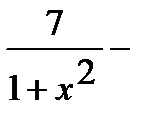
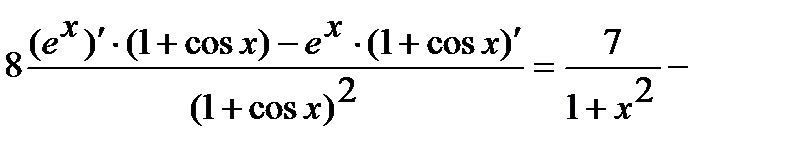
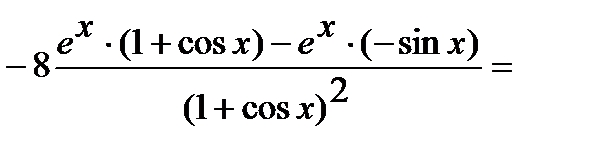
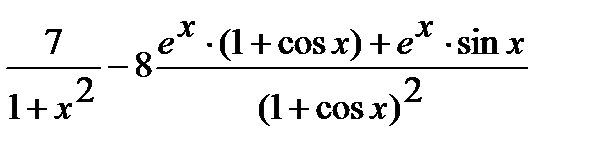 .
.
Дифференцирование сложной функции
Если функция 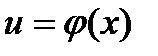 дифференцируема в точке
дифференцируема в точке 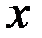 , а функция
, а функция 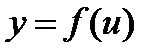 дифференцируема в точке
дифференцируема в точке 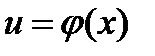 , то сложная функция
, то сложная функция 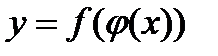 дифференцируема в точке
дифференцируема в точке 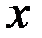 и
и
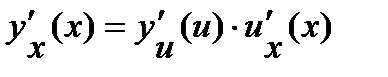 ,
,
где индекс внизу показывает, по какой переменной берется производная.
Задача. Найти производные следующих функций:
а) 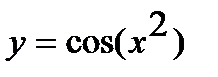 ; г)
; г) 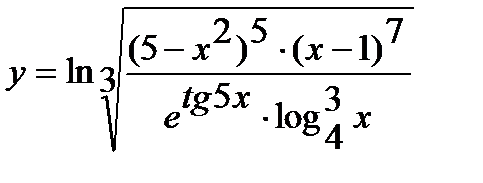 ;
;
б) 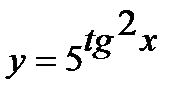 ;
;
в) 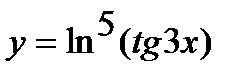 ;
;
Решение. а) Функцию 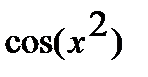 представим как композицию функций
представим как композицию функций 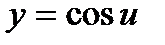 и
и 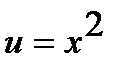 . Используя таблицу производных, находим:
. Используя таблицу производных, находим: 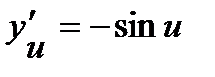 ,
, 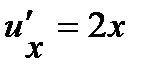 .
.
Тогда
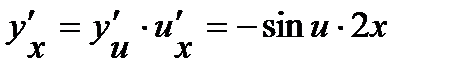
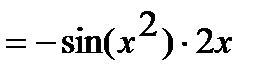 .
.
б) Функцию 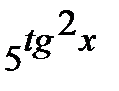 представим как композицию функций
представим как композицию функций 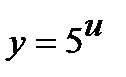 ,
,
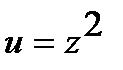 и
и 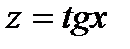 .Найдем производные по промежуточным аргументам:
.Найдем производные по промежуточным аргументам: 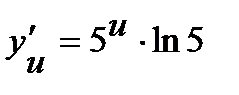 ,
, 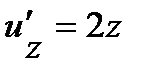 и
и 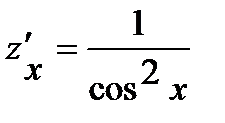 .
.
Производную сложной функции находим по формуле 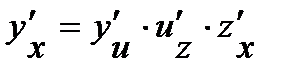 . Окончательно получим
. Окончательно получим 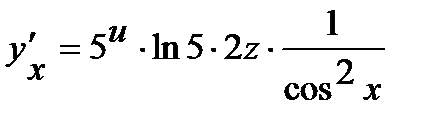 =
= 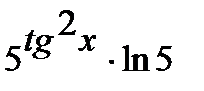
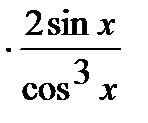 .
.
Аналогично решается задача в:
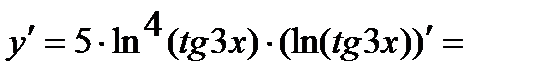
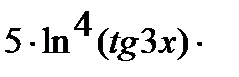
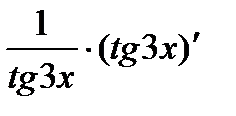 =
=
= 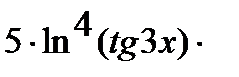
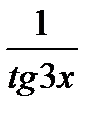

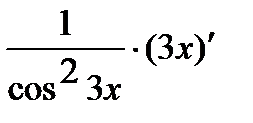 =
= 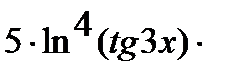
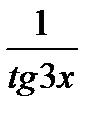
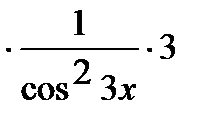 .
.
г) Предварительно упростив выражение, определяющее функцию, до вида
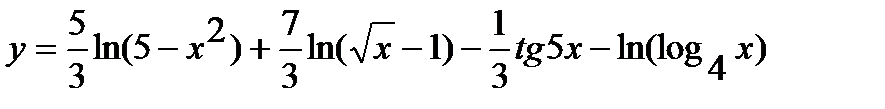 ,
,
находим производную:
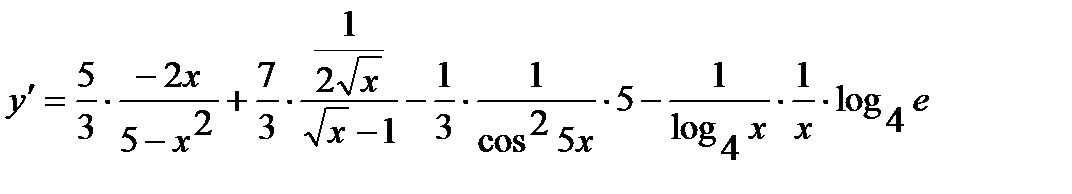 .
.
Методические указания к выполнению
Контрольной работы № 2
