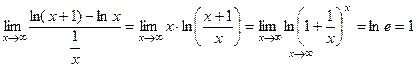Функция. предел функции

3.1. Понятие функции. Основные определения.

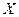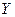О п р е д е л е н и е 1. Пусть даны два числовых множества и . Если каждому 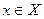по некоторому правилу поставлено некото- рое число 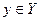, то говорят, что на множестве 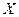задана функция и записывают : 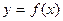, или 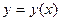. При этом множество 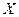называется областью определения функции, а множество 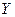- областью значений функции. 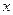называется независимой переменной, или аргументом; 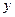- зависимой переменной.

ПРИМЕРЫ:

1. 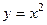- функция заданная на всей числовой прямой

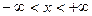. Множество значений этой функции - промежуток 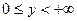. (см. рис. 1)

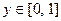2. - эта функция задана на отрезке ; область её значений - . (см. рис. 2)

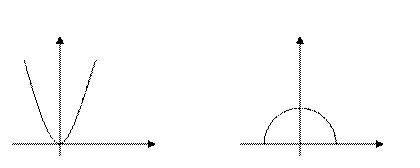
y y

0 x -1 0 1 x

Рис. 1 Рис. 2

3. Эта функция задана на множестве натуральных чисел Множество значений этой функции 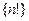содержится в множестве натуральных чисел.

4. Функция Дирихле

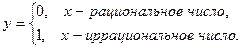
Эта функция задана на всей числовой прямой , а область её значений состоит из двух точек 0 и 1.

5. Функция задана на всей числовой прямой , а множество её значений состоит из тёх точек: -1, 0, +1 (см. рис. 3)

6. 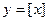- это целая часть действительного числа 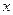. Область определения этой функции - вся числовая прямая, область значений - целые числа. (см. рис. 4)

Y y

1 1

0 x -3 -2 -1 0 1 2 3 4 x

-1

(Рис. 3) (Рис. 4)

3.2 Способы задания функций.

1 Аналитический: Это означает что функция задаётся с помощью какой – либо формулы. Примеры функций из предыдущего пункта заданы аналитически.

2 Табличный. Зависимость между 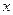и 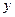задаётся с помощью некоторой таблицы, например,

			….
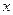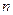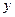	0,34	0,25	…..	0,67

Такие таблицы чаще всего возникают при лабораторных исследования некоторых процессов, чаще всего в физике, химии и т.п. Они задают некоторую закономерность, которую иногда удаётся отобразить аналитически, т.е. удаётся установить закономерность.

3. Графический.. Чаще всего встречается в физике, меди -цине и т.п., когда зависимость между переменными опреде -ляяется с помощью так называемых самопишущих приборов, например, графики на осциллографе, кардиограмма, запись гелиографа, барографа и т.д.

3.3 Классификация функций.

1. Основные элементарные функции:

1) 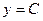- постоянная функция, которая при всех значениях 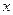принимает одно и то же значение.

2) Степенная функция , где 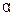- любое действительное число.

3) Показательные функции , в частности, .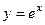

4) Логарифмические функции , , в частности, .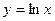

5) Тригонометрические функции: .

6) Обратные тригонометрические функции: .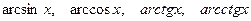

1. Элементарные функции. - это функции, которые получаются из основных элементарных алгебраических операций, или с помощью суперпозиции этих функций. Например: .

Отдельно среди элементарных функций выделяют многочлены, т.е. функции вида:

;

рациональные дроби: , где и 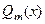- многочлены степен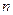и и 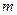, соответственно

и иррациональные функции, т.е. функции, которые содержат хотя бы один корень любого порядка, например, 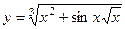и т.п.

3.4. Предел функции

О п р е д е л е н и е 1 Число 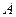называется пределом функции в точке (или при 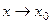), если

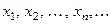для любой сходящейся к точке последовательности значений аргумента 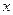( ), соответствующая последовательность 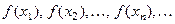значений функции в этих точках сходится к числу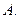

О п р е д е л е н и е 2 Число 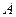называется пределом функции в точке (или при 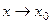), если для любого наперёд заданного 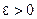можно найти 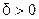, такое что для всех 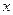( 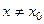), удовлетворяющих неравенству 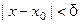, выполняется неравенство .

Можно доказать, что оба эти определения предела последовательности равносильны.

Для обозначения предела функции используется следую- щий символ: .

Замечание. Функция может иметь в точке только один предел, так как последовательность 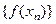может иметь только один предел.

Свойства предела функции.

Пусть 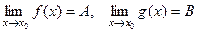. Тогда

1. Функции также имеют пределы в точке , равные соответственно, .
2. Если для всех точек из некоторой окрестности точки выполняется неравенство: 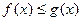, то и для пределов выполняется такое же неравенство, т.е. .
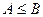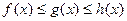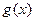3. Если для всех точек некоторой окрестности точки выполняется неравенство и кроме того , то предел функции в точке также существует и равен

Эти свойства автоматически получаются из соответствую- щих свойств предела последовательности, на основании определения 1 предела функции.

3.5. Односторонние пределы.

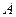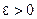О п р е е д е л е н и е 3 Число называется правым (левым) пределом функции в точке , если для любого существует 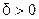такое, что для всех 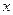, удовлетворяющих неравенству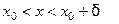 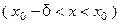, выполняется неравенство .

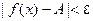Обозначают односторонние пределы следующим образом:

Связь между односторонними пределами и пределом функции устанавливает следующая теорема.

ТЕОРЕМА 1. Функция имеет в точке

предел тогда и только тогда, когда в этой

точке существуют оба односторонних предела

и они равны между собой и равны пределу

функции в этой точке.

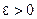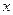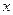Доказательство. Пусть Тогда, согласно определению предела функции, слева и справа, для любого существуют числа и , такие что для всех , удовлетворяющих неравен- ству , и для всех , удовлетворяющих неравенству 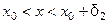, выполняется неравенство 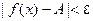. Возьмём 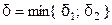. Тогда для всех

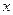, удовлетворяющих неравенствам 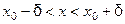, , 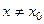или неравенству 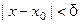, выполняется нера- венство , а это, согласно определению 2, и означает, что . Обратное утверждение оче -видно: если существует предел функции в точке , то существуют и односторонние пределы в этой точке и они равны между собой.

3.6. Предел функции при .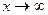

О п р е д е л е н и е 4. Число 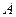называется пределом функции при 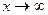, если для любой беско -нечно большой последовательности значений аргу -мента соответствующая последовательность 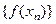зна- чений этой функции сходится к .

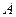Равносильное определение.

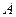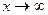О п р е д е л е н и е 5. Число называется пределом функции при , если для любого 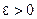существует 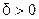, такое что для всех 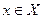, удовле -творяющих неравенству , выполняется неравенство

.

3.7. Два замечательных предела.

! Первый замечательный предел: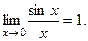

С помощью 1-го замечательного предела можно вычислить многие другие пределы, например:

1)

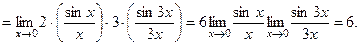
2) сделаем замену переменной

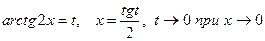, получим

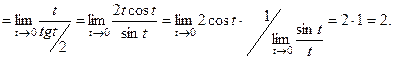
2 Второй замечательный предел.

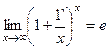, или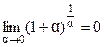

легко получается тз определения числа 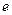(см. 2,4)

С его помощью также можно вычислять многие пределы., например:

1) 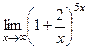сделаем замену 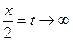при 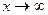, тогда 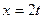и получим

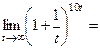
2)

.

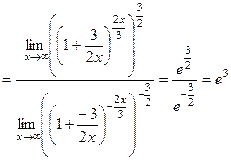3)