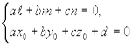Умножение вектора на число

Произведением вектора 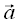на число 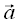и направлен в ту же сторону если 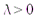( 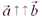) и противоположную сторону если ( ) .

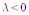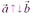Свойства умножения вектора на число:

1⁰. Сочетательное свойство (ассоциативность): 2⁰. Распределительное свойство (дистрибутивность):

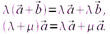
18.

Проекция вектора на ось и ее свойства

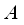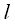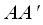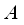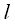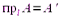Проекцией т. на ось именуется основание перпендикуляра , который опущен из т. на : . Составляющей вектора 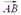по оси 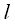является число 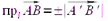. Используется знак (+) , если 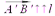, и знак (-) — когда 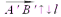.В том случае если 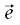является единичным вектором (то есть 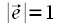) в направлении , то .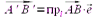

Свойства проекций

1⁰. 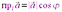, где .

Если 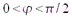, тогда из получаем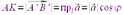

Если 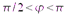, то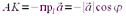

2⁰. Проекция суммы векторов на ось 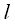равна сумме проекций векторов на .

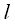Доказательство будет геометрическим.

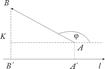
3⁰. 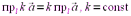. доказательство осуществляется исходя из свойства 1⁰.

19.Разложение вектора на составляющие по осям координат.

Если 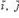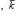- векторы, по модулю равные единице и направленные по координатным осям Ox, Oy и Oz, то разложение вектора 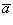по трем координатным осям выражается формулой

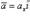
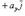
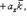
где a_x, a_y и a_z - проекции вектора a на координатные оси - называются координатами вектора (если вектор 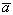имеет координаты a_x, a_y,a_z, то это обозначается так: 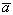{a_x, a_y, a_z}). Если вектор 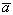имеет начало в начале координат, а его конец A имеет координаты x, y и z, то тогда его проекции на координатные оси равны координатам его конца:

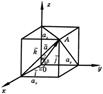
a_x = x; a_y = y; a_z = z.В этом случае вектор называется радиусом-вектором точки A. Радиус-вектор точки обозначается обыкновенно через 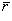(см. рисунок):

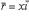
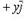
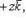(11)

а модуль радиуса-вектора точки A(x, y, z) вычисляется по формуле

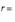
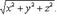(12)

20..Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

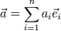
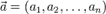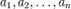где — координаты вектора.

Длиной ненулевого вектора 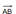называется длина отрезка AB. Длина вектора 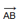(вектора 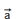) обозначается так: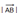 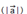. Длина нулевого вектора считается равной нулю: .
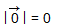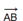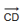Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой ил на параллельных прямых. Если два ненулевых вектора и коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы 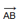и 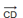называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы 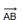и называютсяпротивоположно направленными. Нулевой вектор принято считать сонаправленным с любим вектором.

21.Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:

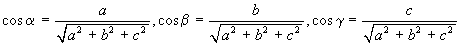
где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.

Сумма квадратов направляющих косинусов равна 1.

22.Коллинеарность векторов.Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.Условия коллинеарности векторов:Два вектора коллинеарные, если отношения их координат равны.Два вектора коллинеарные, если их векторное произведение равно нулю.

Любой вектор коллинеарен нулевому. Вектор a коллинеарен ненулевому вектору bтогда и только тогда, когда эти векторы пропорциональны, т.е. найдется такое число k, что a = kb.Коллинеарные векторы: 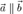Сонаправленные векторы: 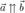Противоположно направленные векторы: 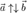Свойства коллинеарности:Пусть 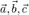— векторы пространства 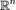. Тогда верны следующие утверждения:Коллинеарность — отношение эквивалентности, то есть оно:1рефлексивно: 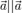2симметрично:

3транзитивно: 4Нулевой вектор коллинеарен любому вектору: 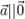5Скалярное произведение коллинеарных векторов равно произведению длин векторов (взятых со знаком «-», если векторы противоположно направлены)6Векторы на плоскости коллинеарны тогда и только тогда, когда их псевдоскалярное произведение равно0.7Коллинеарные векторы линейно зависимы.8Существует действительное число такое, что для коллинеарных 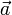и 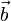, за исключением особого случая . Это определения и также критерий коллинеарности.9На плоскости 2 неколлинеарных вектора 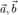образуют базис. Это значит, что любой вектор 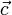можно представить в виде: 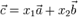. Тогда 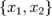будут координатами 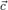в данном базисе.

23. Скалярным произведением двух векторов 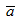и 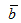называется число, обозночаемое 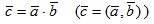и равное произведению модулей данных векторов на косинус угла между ними:

a•b=|a|•|b|•cos(a^b)где (a^b) обозначает меньший угол между направлениями векторов a и b. Отметим, что всегда(0≤a^b≤π).Основные свойства скалярного произведения векторов:
1. a •b = b• a;
2. (λa)•b= •(λb) = λ (a•b);
3. a•(b+с) = a•b+a•с;
4. a•b = | a | прa b = |b| прb| a |;
5. a • a = | a |²;
6. a • b = 0, если a ┴ b.Если a =(x₁, y₁, z₁), b =(x₂, y₂, z₂), то в базисе (i, j, k):
a • b = x₁x₂+ y₁y₂ +z₁z₂, | a | = √x1²+ y1²+ z1², | b | = √x2²+ y2²+ z2².

24.выражение скалярного произведения через координаты

ыражение скалярного произведения через координаты векторов.

Определение 2. Будем говорить, что три вектора 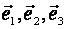в трехмерном пространстве 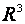образуют ортонормированный базис, если длина каждого из них равна единице и они попарно ортогональны,

Т.е. ,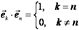

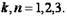
Векторы ортонормированного базиса принято обозначать в : .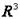

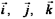Теорема 2. Если векторы 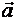и 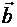заданы своими координатами в базисе : , ,

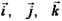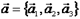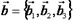То их скалярное произведение определяется формулой: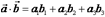

.Доказательство.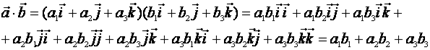

.Т.к.

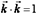
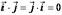
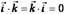
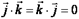
25. Приложения скалярного произведения

Геометрическое и механическое приложение скалярного произведения.А) Необходимым и достаточным условием перпендикулярности векторов 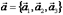, 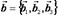является равенство 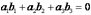(I)

Доказательство. Необходимость: из геометрического свойства 3 имеем, что, если 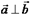, то 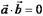, через координаты это выражение принимает вид (I).

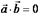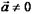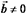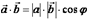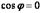
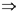
Достаточность. Равенство (I) означает, что , если и , то из равенства , следует что 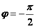, векторы 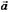и 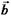взаимно ортогональны. Теорема доказана.

Б) Понятие скалярного произведения имеет свой источник в механике. Если вектор 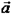изображает силу, точка приложения которой перемещается из начала в конец вектора 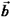, то работа этой силы определяется равенством: .

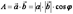26. Векторным произведением векторов 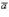и 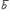называется вектор 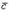, который определяется следующими условиями:

1) Его модуль равен 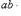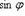где 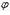- угол между векторам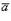и и .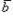

2) Вектор перпендикулярен к плоскости, определяемой перемножаемыми векторами и .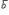

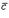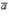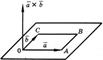3) Вектор направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы и , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок). Векторное произведение векторов и обозначается символом :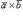

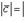
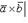
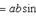
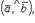(или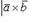

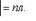
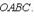
Основные свойства векторного произведения:1) Векторное произведение 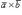равно нулю, если векторы 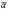и 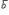коллинеарны или какой-либо из перемножаемых векторов является нулевым.2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):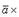

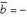
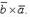
Векторное произведение не обладает свойством переместительности.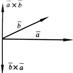

27.Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов i , j и k : если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».Пусть заданы два вектора а=а_хi +a_yj +a_zk и b =b_xi +b_yj +b_zk . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

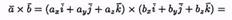
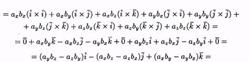
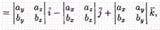
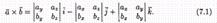
Полученную формулу можно записать еще короче: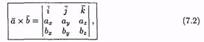

28.Приложения векторного произведения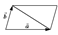

А) Вычисление площадей параллелограмма и треугольника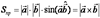

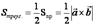
Б) Векторное произведение позволяет проверить коллинеарность двух векторов: .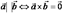

В) Векторное произведение позволяет по двум заданным векторам указать перпендикулярный им вектор.

29.

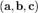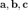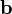Смешанное произведение векторов векторов — скалярное произведение вектора на векторное произведение векторов и 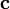: 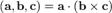Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .

30.Выражение скалярного произведения через координаты векторов.

Будем говорить, что три вектора 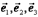в трехмерном пространстве образуют ортонормированный базис, если длина каждого из них равна единице и они попарно ортогональны,Т.е. ,

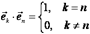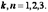
Векторы ортонормированного базиса принято обозначать в : .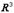

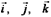Теорема 2. Если векторы 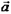и 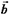заданы своими координатами в базисе : , ,

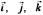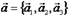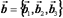То их скалярное произведение определяется формулой: 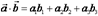Доказательство.

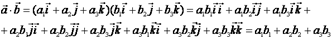
Т.к.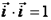

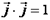
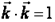
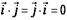
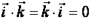
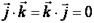
30. приложения смешанного произведения

Определение взаимной ориентации векторов в пространстве.Определение взаимной ориентации векторов а, b и с основано на следующих соображениях. Если abc > 0 , то а , b , с — правая тройка; если abc <0 , то а, b , с - левая тройка.

Установление компланарности векторов.Векторы а, b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю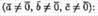

Определение объемов параллелепипеда и треугольной пирамиды.Нетрудно показать, что объем параллелепипеда, построенного на векторах а, b и свычисляется как V =|аbс|, а объем треугольной пирамиды, построенной на этих же векторах, равен V =1/6*|abc |.

31. Объединение множества трёх пересекающихся прямых, в трёх различных точках и множества прямых, каждая из которых пересекает хотя бы две прямые первого множества, но не в точках их пересечений- называется плоскостью.

Общее уравнение плоскости 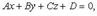где 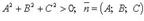- нормальный вектор плоскости.

В векторном виде .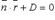

Некоторые характеристические свойства плоскости:Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;2Две плоскости являются либо параллельными, либо пересекаются по прямой.3Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.4Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.5Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.

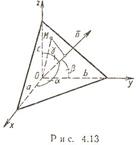
32. Уравнение плоскости, проходящей через три различные точки

|	x - x1	y - y1	z - z1	|
|	x2 - x1	y2 - y1	z2 - z1	|	=
|	x3 - x1	y3 - y1	z3 - z1	|

		|	i	j	k	|
a x b	=	|	X1	Y1	Z1	|
		|	X2	Y2	Z2	|

Если использовать векторные обозначения P₁(x₁,y₁,z₁), P₂(x₂,y₂,z₂), P₃(x₃,y₃,z₃), X(x,y,z), операцию векторного умножения двух векторов а и bа х b = {Y₁Z₂ - Y₂Z₁, Z₁X₂ - Z₂X₁ , X₁Y₂-X₂Y₁}.Для запоминания удобно использовать запись этой формулы через определитель

тогда уравнение плоскости можно переписать в следующем виде

((P₁-P₂) x (P₂-P₁)) ^. (X-P₁) = 0

здесь первое умножение (х) - векторное, второе - скалярное.

33.Уравнение плоскости в отрезках

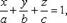где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.

34.Нормальное уравнение плоскости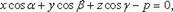
где 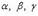- углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.

Приведение общего уравнения плоскости к нормальному виду: 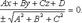Здесь 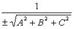- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если 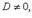произвольно, если D = 0.

35.УГОЛ МЕЖДУ ПЛОСКОСТЯМИРассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

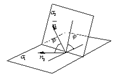
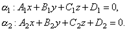
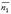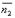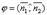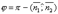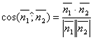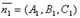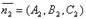Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

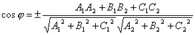Условие параллельности двух плоскостей.Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .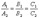

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

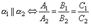или 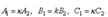Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 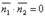или .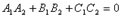

Таким образом, .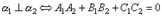

36. Прямая в пространстве.Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

Итак, если уравнения двух непараллельных плоскосте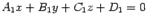й -- и 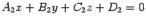, то прямая, являющаяся их линией пересечения, задается системой уравнений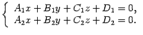

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.Параметрические и канонические уравнения прямой.

Определение. Любой ненулевой вектор, коллинеарный данной прямой называется ее направляющим вектором.

Пусть L – произвольная прямая и 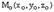– ее произвольная, но фиксированная точка, О – начало координат, 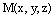– произвольная (текущая) точка прямой L, 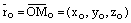– радиус вектор точки 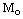, 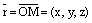– радиус вектор текущей точки М, 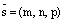– произвольный направляющий вектор прямой L. Следующая система уравнений является параметрическими уравнениями прямой: 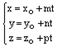(7), ,

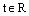где – координаты произвольной фиксированной точки данной прямой, 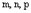– соответствующие координаты произвольного направляющего вектора данной прямой, t – параметр.

Доказательство. В соответствии с определением уравнения любого множества точек координатного пространства, мы должны доказать, что уравнениям (7) удовлетворяют все точки прямой L и, с другой стороны, не удовлетворяют координаты точки не лежащей на прямой.

Пусть произвольная точка 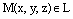. Тогда векторы 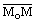и 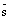являются по определению коллинеарными и по теореме о коллинеарности двух векторов следует, что один из них линейно выражается через другой, т.е. найдется такое числ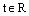о , что 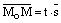. Из равенства векторов 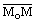и 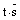следует равенство их координат:

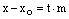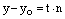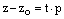, , , ч.т.д.

Следствие. Следующая система уравнений является уравнениями прямой:

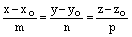. (8)

Определение. Уравнения (8) называются каноническими уравнениями прямой.

37. Уравнение прямой, проходящей через две точки

Пусть в пространстве заданы две точки M₁(x₁, y₁, z₁) и M₂(x_2, y₂, z₂), тогда уравнение прямой, проходящей через эти точки:

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

На плоскости записанное выше уравнение прямой упрощается:если х₁ ¹ х₂ и х = х₁, еслих₁ = х₂.

Дробь = k называется угловым коэффициентом прямой.

38. УравнениеАх+Ву+С=0

(где А, В, С могут иметь любые значения, лишь бы коэффициенты А, В не были нулями оба сразу) представляет прямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.

Если А=0, то есть уравнение не содержит х, то оно представляет прямую, параллельную оси ОХ.Если В=0, то есть уравнение не содержит у, то оно представляет прямую, параллельную оси ОY.Когла В не равно нулю, то общее уравнение прямой можно разрешить относительно ординаты у, тогда оно преобразуется к виду y=ax+b (где a=-A/B; b=-C/B).Аналогично, при А отличным от нуля общее уравнение прямой можно разрешить относительно х.Если С=0, то есть общее уравнение прямой не содержит свободного члена, то оно представляет прямую, проходящую через начало координат.

39.Угол между двумя прямыми и условие Параллельности и перпендикулярность прямых

равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле: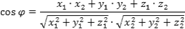

Условия параллельности двух прямых:а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:k₁ = k₂.

б) Для случая, когда прямые заданы уравнениями в общем виде, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.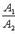

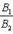
5. Условия перпендикулярности двух прямых:а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е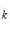

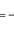
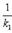
40.Плоскость и прямая в пространстве.Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0 задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением , которое называется уравнением плоскости.Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости.Если две прямые лежат в одной плоскости, угол между ними легко измерить — например, с помощью транспортира. А как измерить угол между прямой и плоскостью?

Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.

Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получилипроекцию наклонной на плоскость.

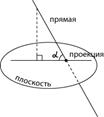Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.признак перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Параллельность прямой и плоскости.Прямая и плоскость могут пересекаться или быть параллельными друг другу. Еще один случай — прямая лежит в плоскости.Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.признак параллельности прямой и плоскости:

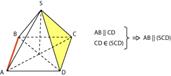
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. 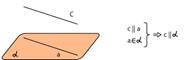Этот признак часто используется в решении задач по стереометрии. Например, в правильной четырехугольной пирамиде SABCD прямая АВ параллельна прямой СD — значит, АВ параллельна всей плоскости SCD.

41. Пересечение прямой и плоскости.Для рассмотрения пересечения прямой и плоскости целесообразно начать с рассмотрения случая пересечения двух плоскостей (рис. 3.9), когда одна из пересекающихся плоскостей параллельна горизонтальной плоскости проекций (α | | π₁, f⁰_α | | Х). В этом случае линия пересечения а, принадлежащая плоскости α, будет также параллельна плоскости π₁, (рис. 3.9. а), т. е. будет совпадать с горизонталью пересекающихся плоскостей (а ≡ h).

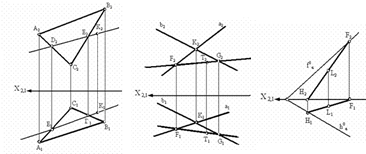
а б в

Рис. 3.8. Прямые, параллельные плоскостям, заданным:
а - плоскостью треугольника АВС;
б - двумя пересекающимися прямыми а ∩ b;
в - горизонтальным h⁰_α и фронтальным f⁰_α следами

Условие принадлежности прямой плоскости