Основные свойства неопределенного интеграла
I Дифференциал неопределенного интеграла равен подынтегральному выражению
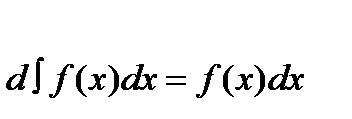
II Неопределенный интеграл от дифференциала функции равен этой функции сложенной с постоянной интегрирования
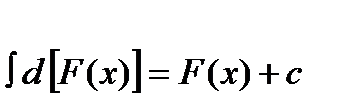
III Постоянный множитель можно вынести за знак интеграла
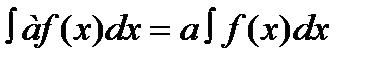
IV Интеграл от суммы функций равен сумме интегралов от каждой из них.
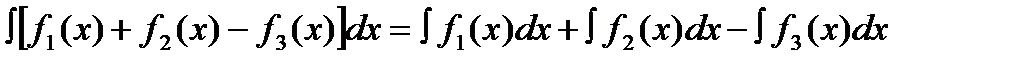
Основные формы интегрирования
1. 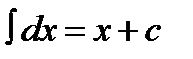
2. 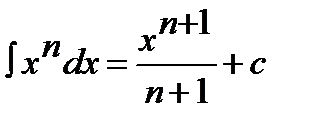 n≠-1
n≠-1
3. 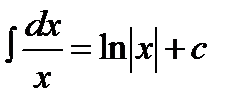
4. 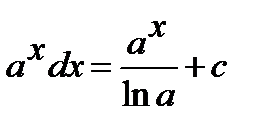 a>0 n≠1
a>0 n≠1
5. 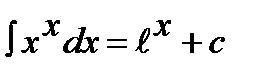
6. 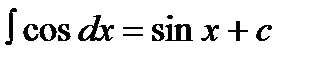
7. 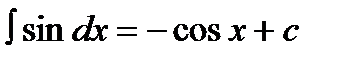
8. 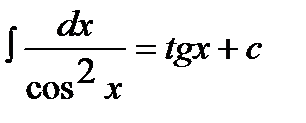
9. 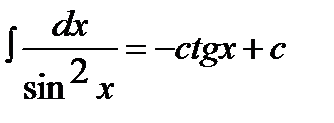
10. 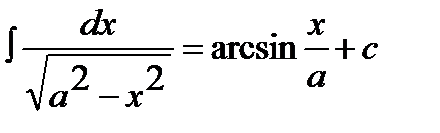
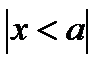 a ≠ 0
a ≠ 0
11. 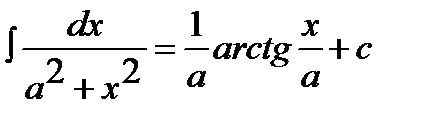 a ≠ 0
a ≠ 0
12. 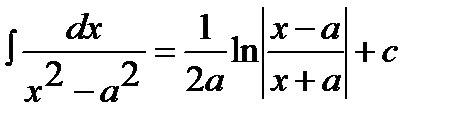 a ≠ 0
a ≠ 0
Решить в аудитории
1. 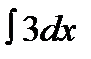 10.
10. 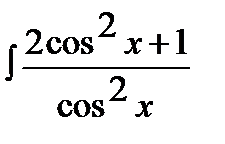
2. 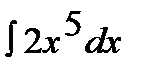 11.
11. 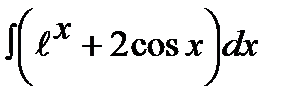
3. 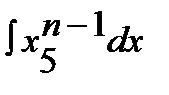 12.
12. 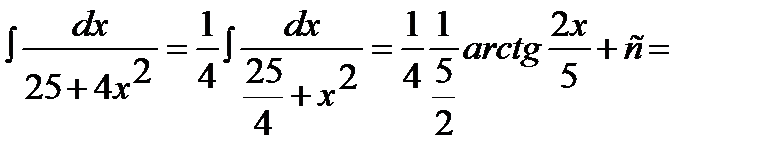
4. 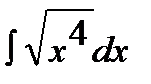
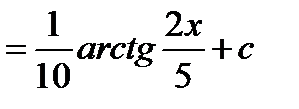
5. 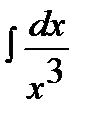
6. 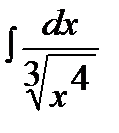
7. 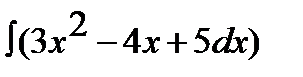
8. 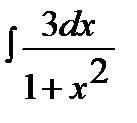
9. 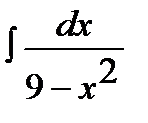
Домашнее задание
1. 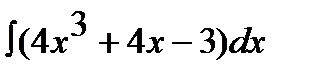
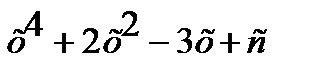
2. 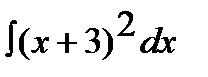
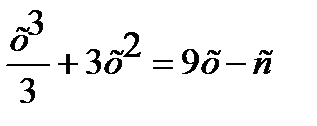
3. 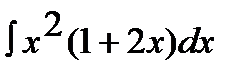
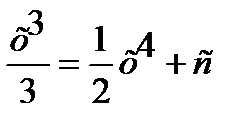
4. 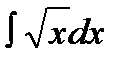
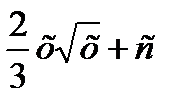
5. 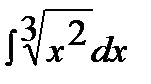
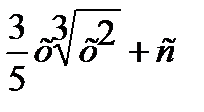
6. 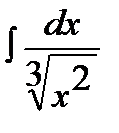
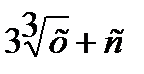
7. 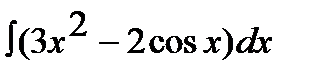
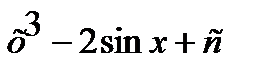
8. 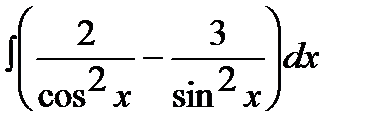
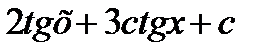
9. 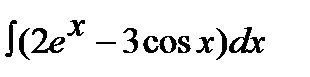
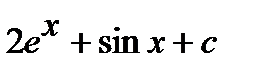
10. 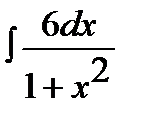
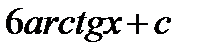
Урок № 71. Тема 8.2.: Площадь криволинейной трапеции. Определенный интеграл.
План.
1. Площадь криволинейной трапеции.
2. Определенный интеграл
Рассмотрим функцию у=f(x)xЄ[a;в]
Фигура АавВ называется криволинейной трапецией.
Выразим площадь данной трапеции. Для чего разобьем на n равных частей отрезок [a;в]. Получим отрезки [a;х1], [х1;х2]….. [хn1;в]
Через mi и Mi обозначим наибольшее и наименьшее значения функции f(x) на любом отрезке [хi-1;xi].
Криволинейная трапеция АавВ разбивается на n частей. Очевидно, площадь i-ой части не меньше mi(xi-xi-1) и не больше Мi(xi-xi-1), следовательно, площадь криволинейной трапеции не меньше суммы m1∆x1+m2∆x2+….+mn∆xn= 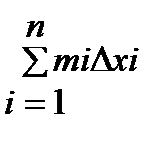 где ∆хi=xi-1 и не больше суммы М1∆x1+М2∆x2+….+Мn∆xn=
где ∆хi=xi-1 и не больше суммы М1∆x1+М2∆x2+….+Мn∆xn= 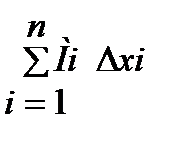 . Обозначим эти суммы sn и Sn, получим
. Обозначим эти суммы sn и Sn, получим
Sn≤SAaвB≤Sn.
В последнем неравенстве слева площадь ступенчатой функции, которая содержится в данной криволинейной трапеции, а справа – площадь ступенчатой функции, которая содержит данную криволинейную трапецию.
При n→∞ 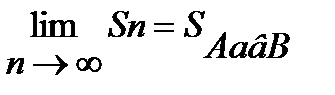
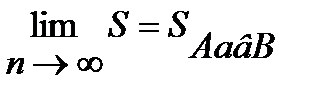
Рассмотрим снова криволинейную трапецию АавВ разбитую на n отрезков. Выберем на i-ом отрезке произвольную точку γi. Пусть mi и Mi наименьшее и наибольшее значения функции f(x) на отрезке [xi-1; xi] и очевидно mi≤f(ηi)≤Mi. Умножим каждый член данного неравенства на ∆хi=xi=xi-1 и просуммируем почленно, получим:
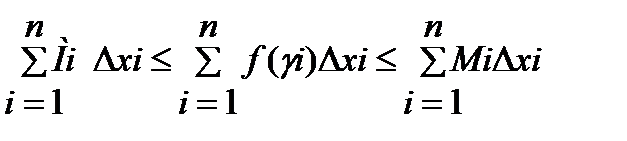
Очевидно, 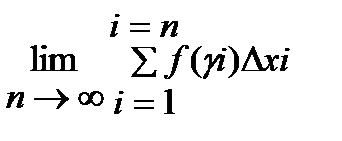 существует и не зависит от выбора точки γi т.о.
существует и не зависит от выбора точки γi т.о. 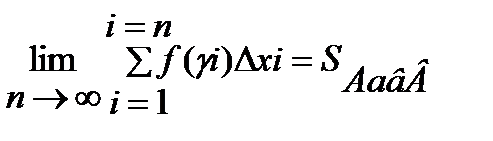
Определенный интеграл
Сумма 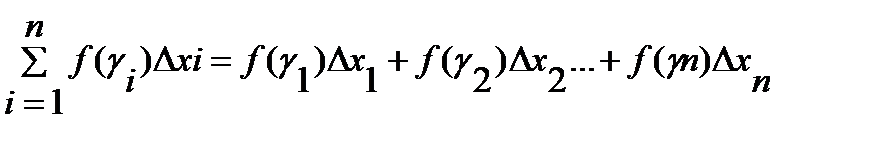
где ∆хi=xi-xi-1 называется интегральной.
Определение. Если предел 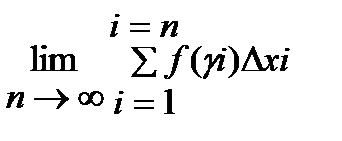 существует и не зависит от выбора точки γi, то функция f(x) называется интегрируемой на отрезке [а, в], а предел называется определенным интегралом от функции f(x) на отрезке [а, в] и обозначается
существует и не зависит от выбора точки γi, то функция f(x) называется интегрируемой на отрезке [а, в], а предел называется определенным интегралом от функции f(x) на отрезке [а, в] и обозначается 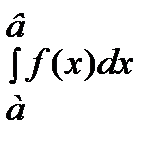 .
.
Читается: интеграл от а до в от 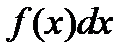
а – нижний предел интегрирования
в – верхний предел интегрирования
и так 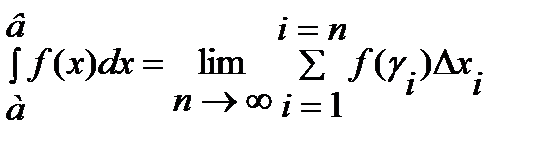
Закрепление нового материала.
Домашнее задание – выучить конспект.
Урок № 72. Тема 8.3.: Свойства определенного интеграла. Вычисление определенного интеграла.
План.
Свойства определенного интеграла.
Вычисление определенного интеграла.
