Основные свойства неопределенного интеграла.

1) Производная неопределенного интеграла равна подынтегральной функции.

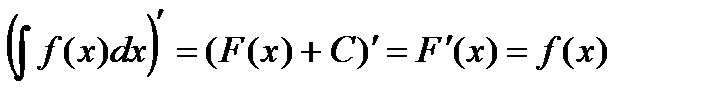
2) Дифференциал неопределенного интеграла равен подынтегральному выражению.

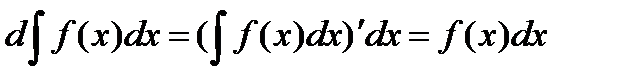
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.

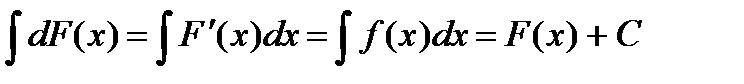
Свойства 1) и 2) используют обычно для проверки результатов интегрирования.

4) Постоянный множитель можно выносить за знак интеграла, т. е. если 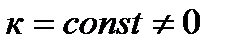, то

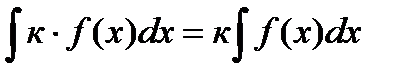
5) Неопределенный интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме интегралов от этих функций в отдельности, т. е.

.

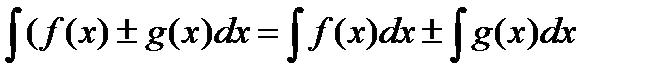Таблица основных интегралов.

Из определения неопределенного интеграла следует, что если 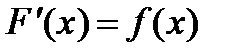то 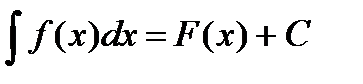. Исходя из этого и используя формулы дифференцирования, можно составить следующую таблицу неопределенных интегралов.

1.

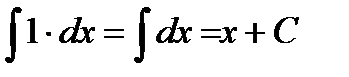
2.

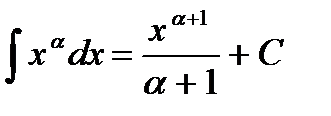
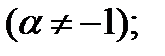
3. ,

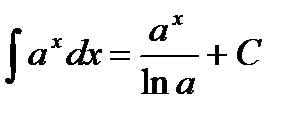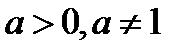
4.

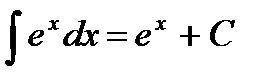
5.

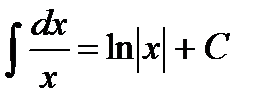
6.

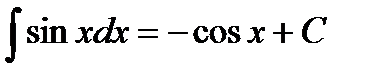
7.

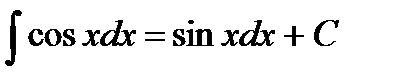
8.

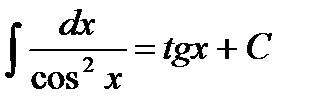
9.

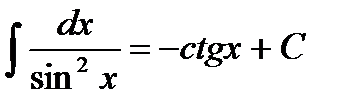
10.

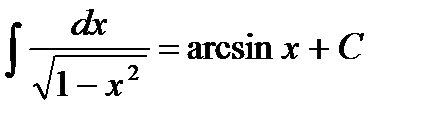
11.

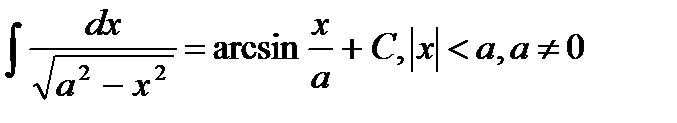
12.

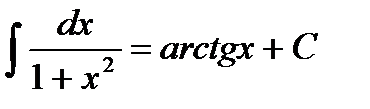
13.

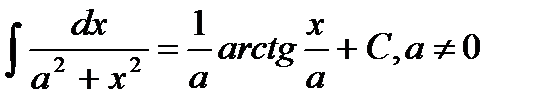
14.

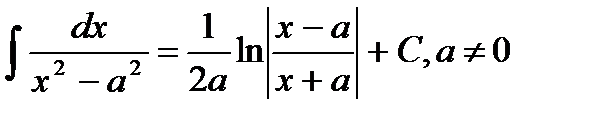
15. .

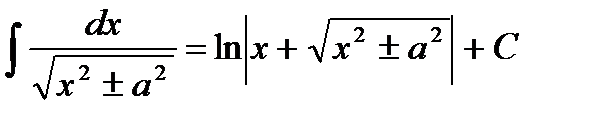Пример 1. Найти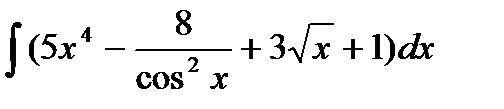

Применив свойства 4) и 5) и табличные интегралы 1,2 и 8, находим

.

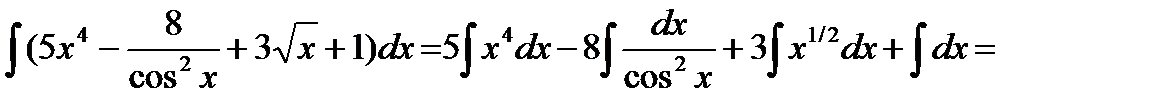
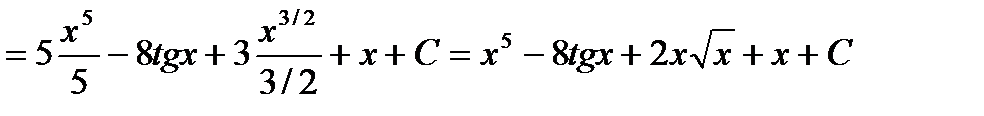Пример 2.Найти .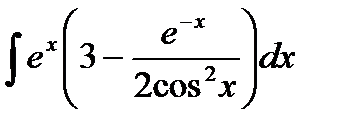

Раскрывая скобки и применяя табличные интегралы 4 и 8, найдем

.

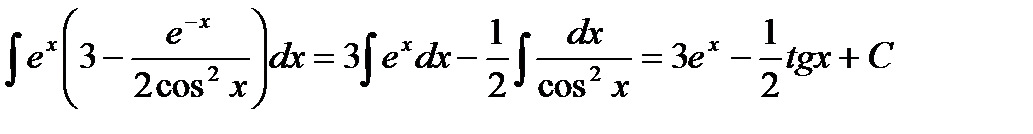Интегрирование методом замены переменной (методом подстановки).

Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных приемов является метод подстановки или замены переменной интегрирования. Сущность этого метода заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому интегралу, который сравнительно легко берется непосредственно. Рассмотрим этот метод.

Пусть функция 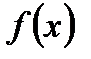непрерывна на промежутке 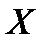и 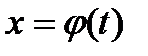, где функция 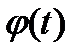непрерывно дифференцируема на промежутке 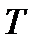и имеет область значений 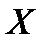. Пусть также функция 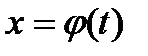имеет обратную 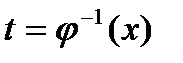, 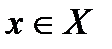. Тогда

.

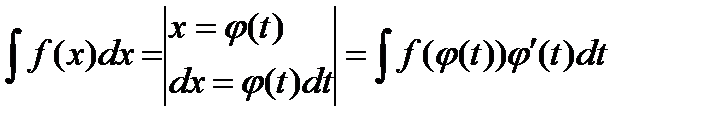После вычисления интеграла в правой части следует вернуться к старой переменной 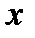, то есть вместо новой переменной 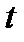подставить его значение .

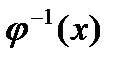Если интеграл имеет вид 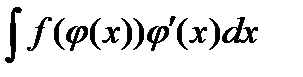, то его вычисление можно проводить следующим образом:

.

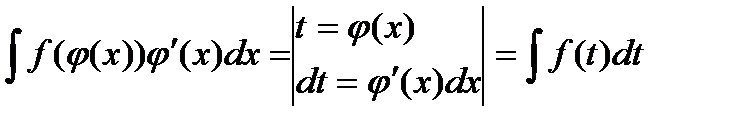Пример. .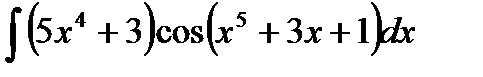

Решение.

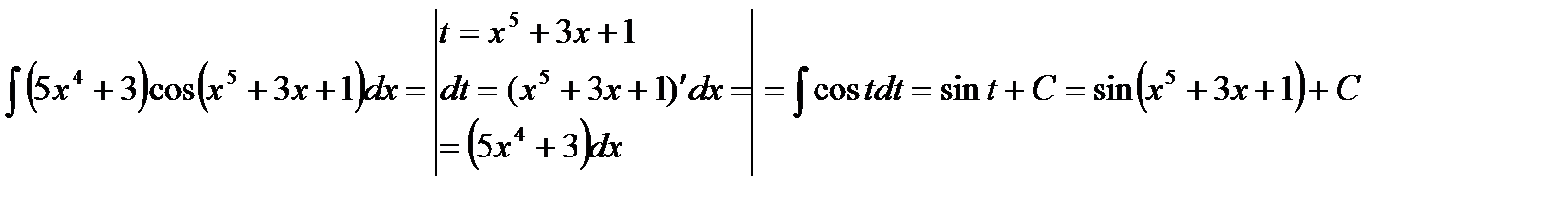
Пример. .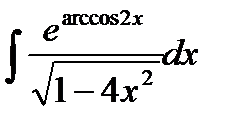

Решение.

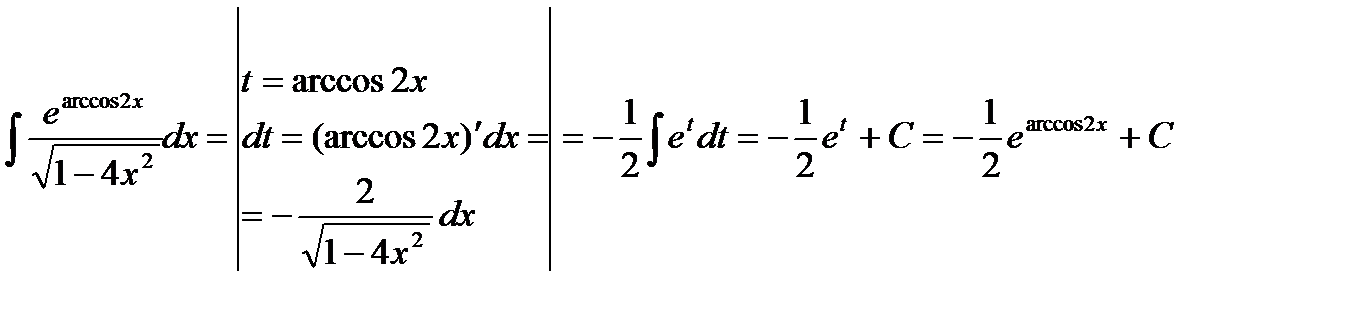
Интегрирование по частям.

Пусть функци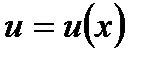и и 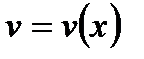имеют непрерывные производные на некотором промежутке 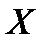. Найдем дифференциал произведения этих функций:

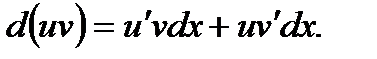
Так как по условию функци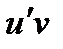и и 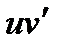непрерывны, можно проинтегрировать обе части этого равенства,

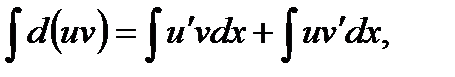
или

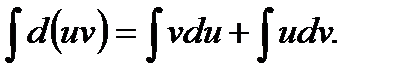
Но 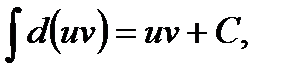следовательно,

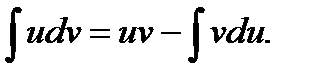(1)

В правой части формулы (1) постоянную интегрирования С не пишут, так как она фактически присутствует в интеграле 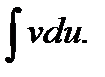Формула (1) называется формулой интегрирования по частям.

Сущность метода интегрирования по частям вполне соответствует его названию. Дело в том, что при вычислении интеграла этим методом подынтегральное выражение 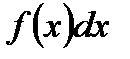представляется в виде произведения множителе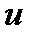й и 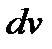; при этом 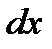обязательно входит в 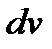. В результате получается, что заданный интеграл находят по частям: сначала находят 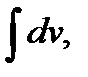а затем 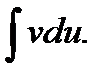Естественно, что этот метод применим лишь в случае, если задача нахождения указанных двух интегралов более проста, чем нахождение заданного интеграла.

Пример.Найти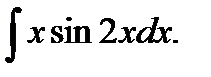

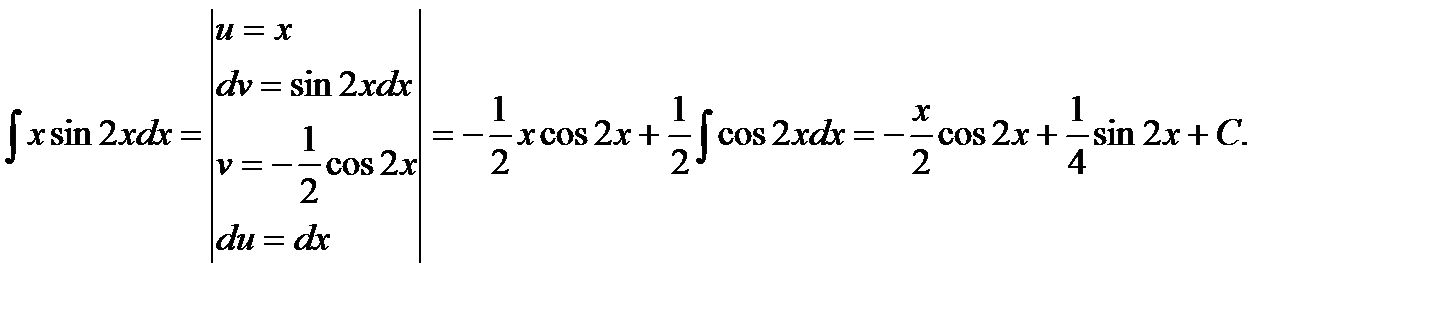
При вычислении интегралов методом интегрирования по частям главным является разумное разбиение подынтегрального выражения на множител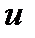и и 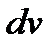. Общих установок по этому вопросу не имеется. Однако для некоторых типов интегралов, вычисляемых методом интегрирования по частям, сделать это возможно.

1. В интегралах вида

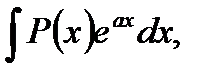
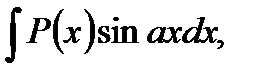
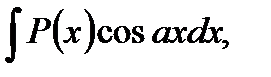
где 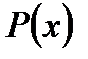- многочлен относительно 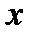, 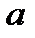- некоторое число, полагают 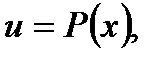а все остальные сомножители за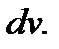

Пример 2.Найти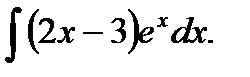

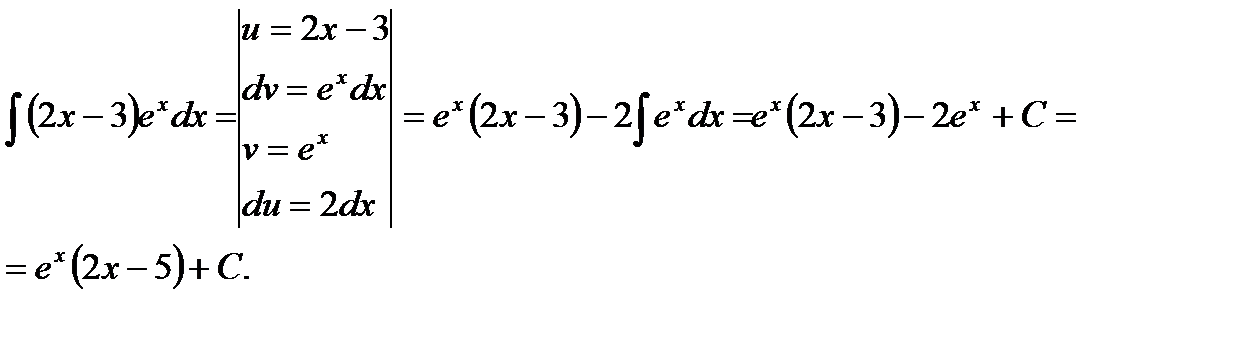
2. В интегралах вида

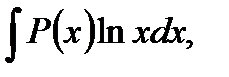
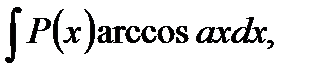
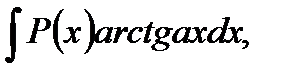
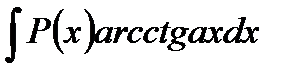
полагают 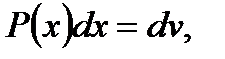а остальные сомножители – за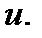

Пример 3.Найти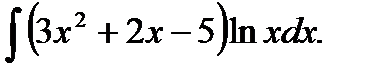

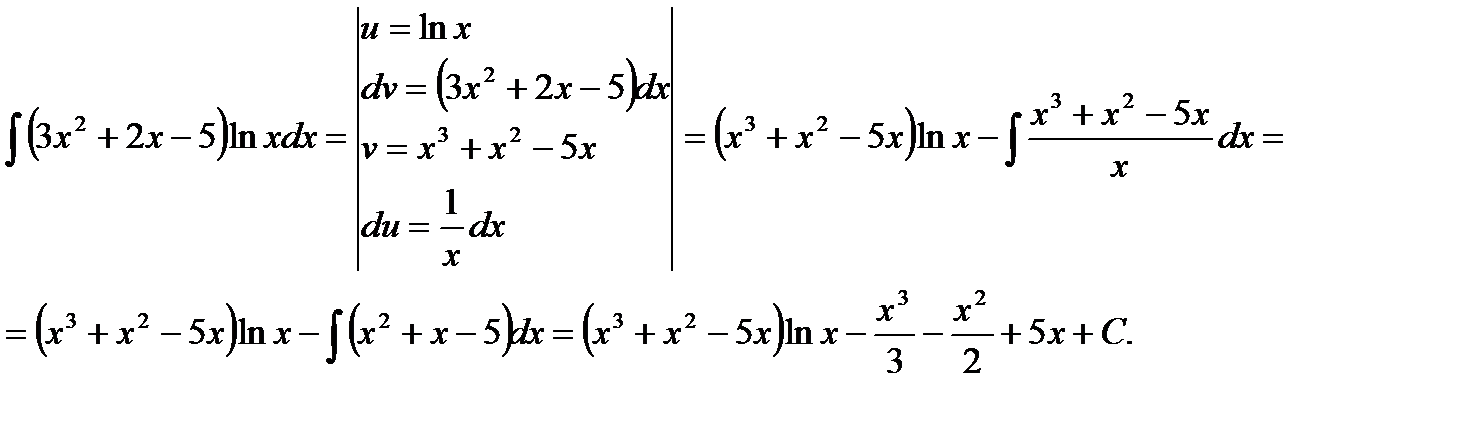
3. В интегралах вида

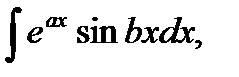
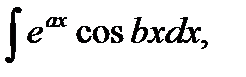
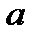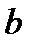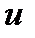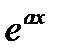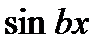где и - числа, за можно принять любую из функций или (или 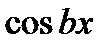). Однако метод интегрирования по частям придется применять дважды, выбирая оба раза за 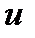одну и ту же функцию 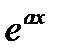или тригонометрические функции 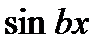, 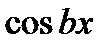. В результате двукратного применения формулы (1) в правой части равенства появится искомый интеграл, который находится путем решения простого алгебраического уравнения.

Пример 4.Найти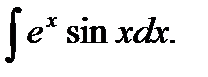

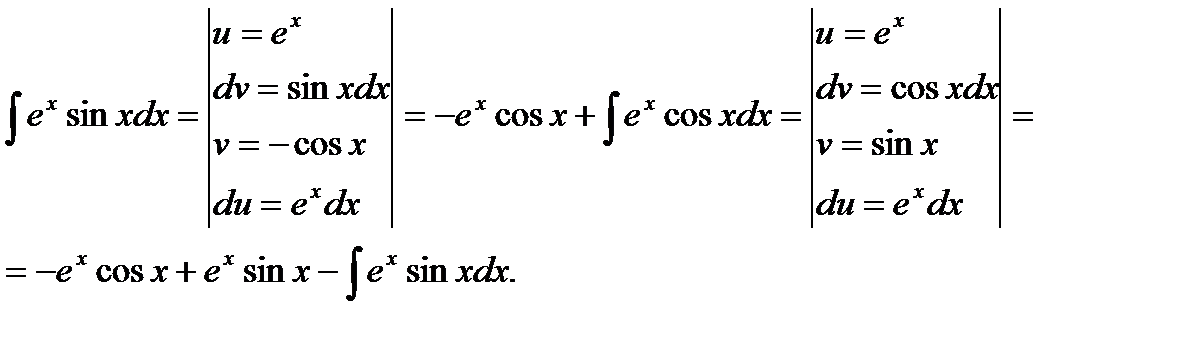
Так как в правой части стоит искомый интеграл, то, перенеся его в левую часть, получим

.

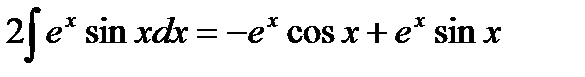Отсюда получаем окончательный результат:

.

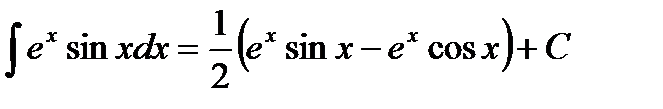Определенный интеграл.

Пусть функция 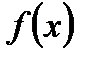определена и непрерывна на отрезке 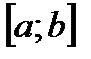. В плоскости ХОУ дана криволинейная трапеция ABCD, ограниченная отрезком 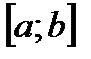, осью ОХ, прямыми 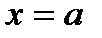, 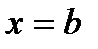и графиком функции 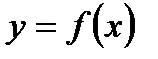. Требуется определить площадь 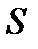этой криволинейной трапеции. Для решения этой задачи поступаем следующим образом. Разобьем отрезок 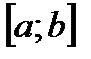оси ОХ на 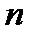элементарных отрезков точками
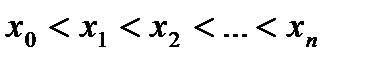( ). Через точки деления проведем вертикальные прямые. При этом криволинейная трапеция ABCD разобьется на 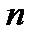криволинейных трапеций с основаниями 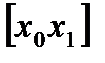, , 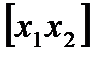, 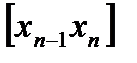. В каждом из отрезков 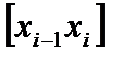, 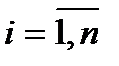зафиксируем произвольную точку 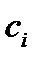( 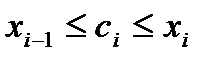) и построим прямоугольник с основанием 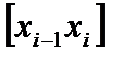и высотой 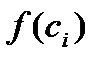. Его площадь равна 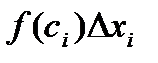, где .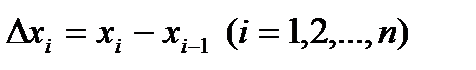

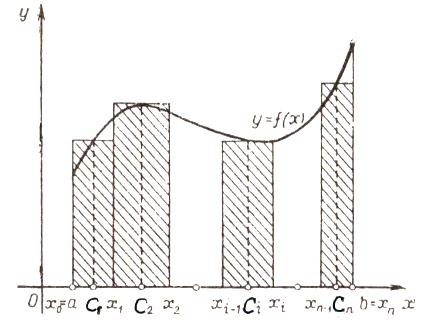
Рассмотрим ступенчатую фигуру, составленную из прямоугольников с основаниями 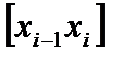, 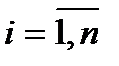. Ее площадь 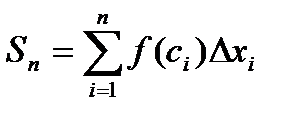приближенно равна площади 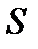криволинейной трапеции ABCD 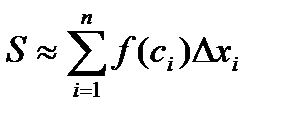. Сумма 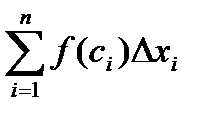называется интегральной суммой для функции .

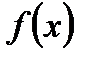За площадь криволинейной трапеции естественно принять предел, к которому стремятся площади построенных указанным образом ступенчатых фигур при неограниченном уменьшении наибольшей длины элементарных отрезков ( 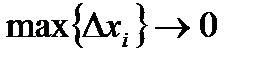) и, соответственно, неограниченном увеличении числа этих отрезков ( ):

, , .

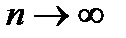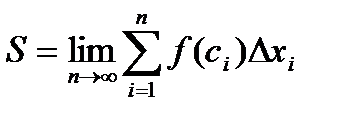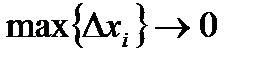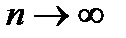Определение. Если при неограниченном уменьшении наибольшей длины элементарных отрезков ( 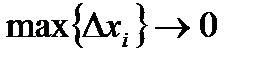) и соответственно, при неограниченном увеличении числа этих отрезков 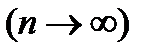интегральная сумма 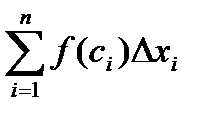имеет конечный предел, не зависящий ни от способа разбиения отрезка 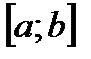на элементарные отрезки, ни от выбора точек 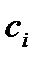, ни от способа суммирования, то такой предел называется определенным интегралом от функции 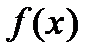на отрезке 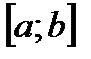и обозначается .

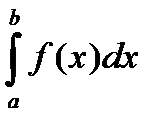Итак, по определению

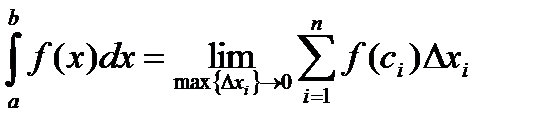(1)

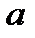Здесь и 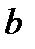соответственно нижний и верхний пределы интегрирования, 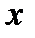- независимая переменная, 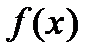- подынтегральная функция, 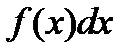- подынтегральное выражение.

Заметим без доказательства, что если подынтегральная функция 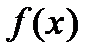непрерывна на отрезке 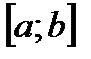, то определенный интеграл от этой функции на 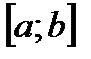существует.

Определение. Функция 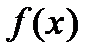называется интегрируемой на отрезке 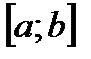, если интеграл от этой функции на 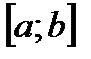существует.

Если интегрируемая на отрезке 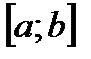функция 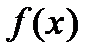неотрицательна, то определенный интеграл 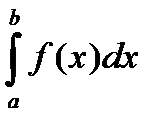численно равен площади S криволинейной трапеции, ограниченной графиком функции 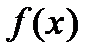, осью абсцисс и прямым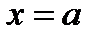и и 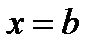(см. рис. 2), т. е. 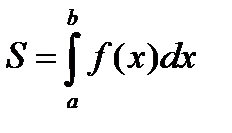(2)

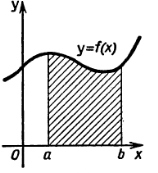
Рис. 2

В этом заключается геометрический смысл определенного интеграла.

Если во всех точках отрезка 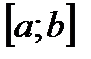функция 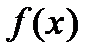неположительна, т.е. 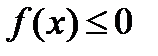для 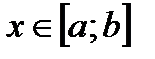, то правая часть в формуле (1) также определяет площадь соответствующей криволинейной трапеции, но взятой со знаком —, т.е.

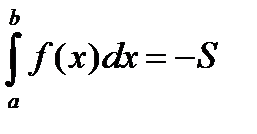
При введении понятия определенного интеграла как предела интегральных сумм мы допустили, что 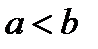. В случае 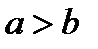примем, по определению,

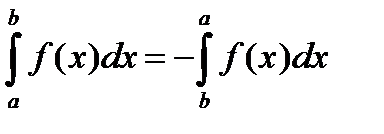(3)

При 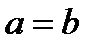также по определению, полагаем

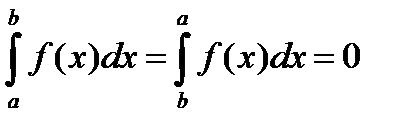(4)

Следует заметить, что определенный интеграл зависит только от интегрируемой функции 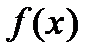и пределов интегрирования 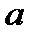и 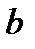, но не от того, какой буквой обозначается переменная интегрирования. Поэтому

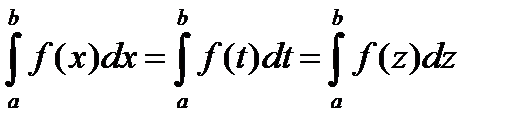(5)

и т.д.