Первообразная функция и неопределенный интеграл. Основные свойства неопределенного интеграла
Первообразная функция.
Определение: Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
Определение: Неопределенным интеграломфункции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 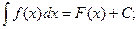
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 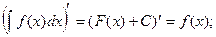
2. 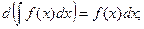
3. 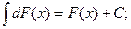
4. 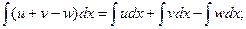 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
1. 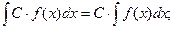
Таблица основных формул и правил интегрирования.
Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.
| Интеграл | Значение | Интеграл | Значение | ||
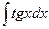 | -ln½cosx½+C | 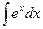 | ex + C | ||
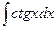 | ln½sinx½+ C | 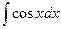 | sinx + C | ||
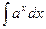 | 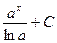 | 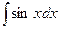 | -cosx + C | ||
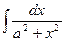 | 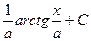 | 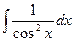 | tgx + C | ||
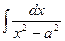 | 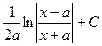 | 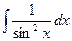 | -ctgx + C | ||
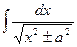 | ln 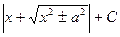 | 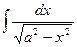 | arcsin 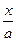 + C + C | ||
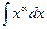 | 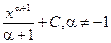 | 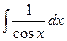 | 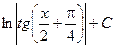 | ||
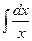 | 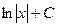 | 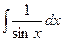 | 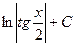 |
9.Основные методы интегрирования: непосредственное, замена переменной, по частям.
Методы интегрирования.
Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти значение интеграла 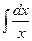 . На основе известной формулы дифференцирования
. На основе известной формулы дифференцирования 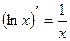 можно сделать вывод, что искомый интеграл равен
можно сделать вывод, что искомый интеграл равен 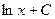 , где С – некоторое постоянное число. Однако, с другой стороны
, где С – некоторое постоянное число. Однако, с другой стороны 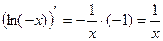 . Таким образом, окончательно можно сделать вывод:
. Таким образом, окончательно можно сделать вывод:
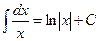
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 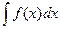 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
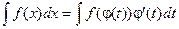
Доказательство: Продифференцируем предлагаемое равенство:
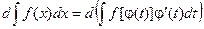
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[j(t)]j¢(t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 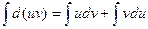 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
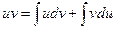 или
или 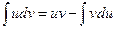 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
10 Интегрирование выражений, содержащих квадратный трехчлен.
Рассмотрим интеграл 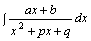 , содержащий квадратный трехчлен в знаменателе подынтегрального выражения. Такой интеграл берут также методом подстановки, предварительно выделив в знаменателе полный квадрат. Покажем это на примерах.
, содержащий квадратный трехчлен в знаменателе подынтегрального выражения. Такой интеграл берут также методом подстановки, предварительно выделив в знаменателе полный квадрат. Покажем это на примерах.
11.Рациональные дроби. Простейшие рациональные дроби и их интегрирование.
Интегрирование элементарных дробей.
Определение: Элементарныминазываются дроби следующих четырех типов:
I. 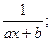 III.
III. 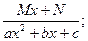
II. 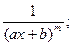 IV.
IV. 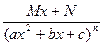
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. 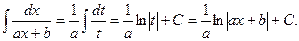
II. 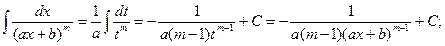
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:
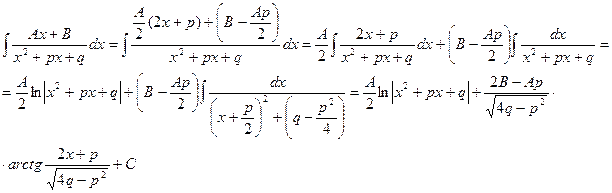
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида 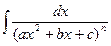 можно путем выделения в знаменателе полного квадрата представить в виде
можно путем выделения в знаменателе полного квадрата представить в виде 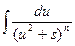 . Сделаем следующее преобразование:
. Сделаем следующее преобразование:
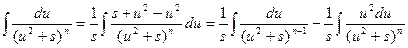 .
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 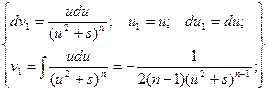
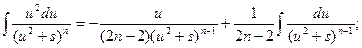
Для исходного интеграла получаем:
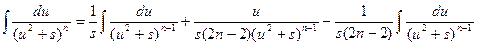
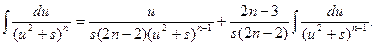
Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл 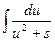 .
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
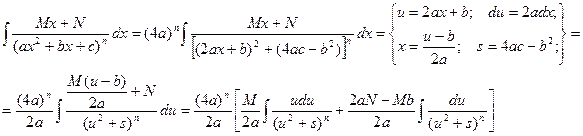
В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному 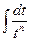 , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
, а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
12.Разложение рациональной дроби на простейшие. Интегрирование рациональных дробей.
Интегрирование рациональных дробей.
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема: Если 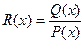 - правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
- правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
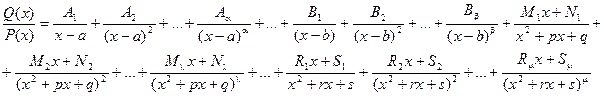
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
