Моделирование рисков инвестиционных проектов

Имитационное моделирование представляет собой серию численных экспериментов призванных получить эмпирические оценки степени влияния различных факторов (исходных величин) на некоторые зависящие от них результаты (показатели).

В общем случае, проведение имитационного эксперимента можно разбить на следующие этапы.

Установить взаимосвязи между исходными и выходными показателями в виде математического уравнения или неравенства.

Задать законы распределения вероятностей для ключевых параметров модели.

Основные законы распределения непрерывных случайных величин

Равномерный закон распределения.

СВ X распределена по рав­номерному (прямоугольному) закону, если все значения СВ лежат внутри некоторого интервала и все они равновероятны (точнее, обла­дают одной плотностью вероятности). Например, если весы имеют точность 1г и полученное значение округляется до ближайшего цело­го числа к, то точный вес можно считать равномерно распределенной СВ на интервале (t-0,5; к+0,5).

Дифференциальная функция равномерного закона на интервале ( 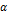, 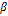) (рис.11):

f(x) =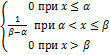

Интегральная функция равномерного закона на интервале (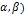

F(x) =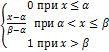

Дифференциальная функция Интегральная функция

Рис. Равномерный закон распределения

1. Математическое ожидание:

M(X) .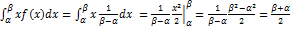

М(Х) совпадает, в силу симметрии распределения, с медианой.

2. Моды равномерное распределение не имеет.

3. Дисперсия D(X) = =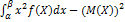

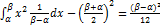
4. Вероятность попадания СВ в заданный интервал (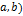

.

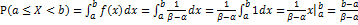Показательное распределение. НСВ X, принимающая неотрица­тельные значения, имеет показательное распределение, если ее диф­ференциальная функция имеет вид:

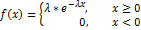
Интегральная функция показательного закона

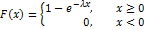
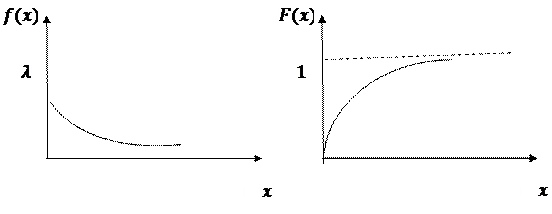Дифференциальная функция Интегральная функция

Рис. Показательный закон распределения

Нормальный закон распределения (рис. 14) играет исключи­тельную роль в теории вероятностей. Это наиболее часто встречаю­щийся закон распределения, главной особенностью которого — то, что он является предельным законом, к которому, при определенных ус­ловиях, приближаются другие законы распределения.

Дифференциальная функция нормального закона имеет вид:

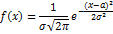
M(X)=a – характеризует центр распределения

D(X)= 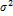– характеризует форму распределения

Вероятность попадания нормальной случайной величины в заданный интервал определяется по свойству интегральной функции:

P(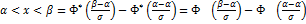

где 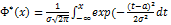- интегральная функция нормального закона, Ф(x) – функция Лапласа

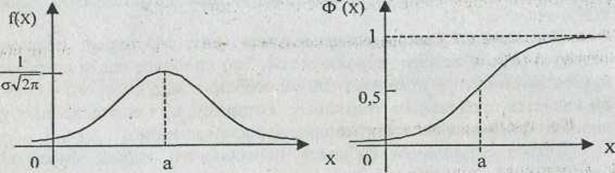
Дифференциальная функция Интегральная функция

Рис. Нормальный закон распределения