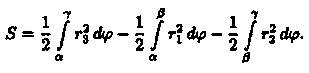Вычисление площадей плоских фигур

Прямоугольные координаты

Как уже было установлено (см. «геометрический смысл определенного интеграла»), площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному интегралу:

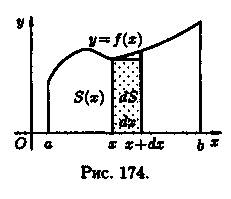
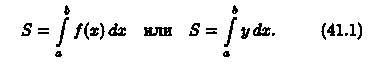
Формула (41.1) получена путем применения схемы I — метода сумм. Обоснуем формулу (41.1), используя схему II. Пусть криволинейная трапеция ограничена линиями у = ƒ(х) ≥ 0, х = а, х = b, у = 0 (см. рис. 174).

Для нахождения площади S этой трапеции проделаем следующие операции:

1. Возьмем произвольное х Î [а; b] и будем считать, что S = S(x).

2. Дадим аргументу х приращение Δх = dx (х + Δх є [а; b]). Функция S = S(x) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).

Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у • dx.

3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем

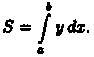
Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь может быть найдена по формуле

Формулы (41.1)и (41.2) можно объединить в одну:

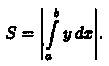
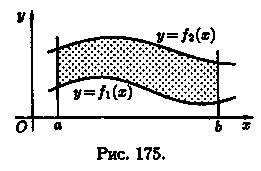
Площадь фигуры, ограниченной кривыми у = = fι(x) и у = ƒг(х), прямыми х = а и х = b (при условии ƒ2(х) ≥ ƒ1(х)) (см. рис. 175), можно найти по формуле

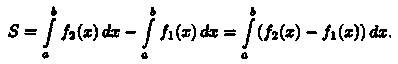
Если плоская фигура имеет «сложную» форму (см. рис. 176), то прямыми, параллельными оси Оу, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.

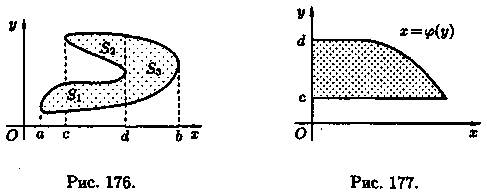
Если криволинейная трапеция ограничена прямыми у = с и у=d, осью Оу и непрерывной кривой х = φ(у) ≥ 0 (см. рис. 177), то ее площадь находится по формуле

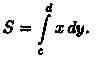
И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически

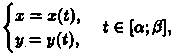
прямыми х = а и х = b и осью Ох, то площадь ее находится по формуле

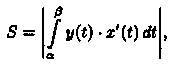
где а и β определяютсяиз равенств х(а) = а и х(β) =b.

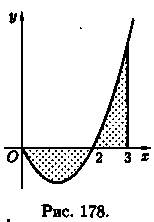
Пример 41.1. Найти площадь фигуры, ограниченной осью Ох и графиком функции у = х2 - 2х при х є [0; 3].

Решение: Фигура имеет вид, изображенный на рисунке 178. Находим ее площадь S:

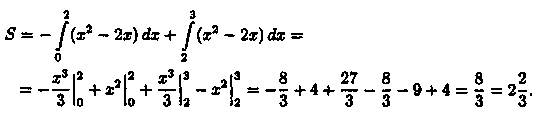
Пример 41.2. Вычислить площадь фигуры, ограниченной эллипсом х = а cos t, у = b sin t.

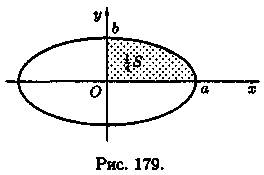Решение: Найдем сначала 1/4 площади S. Здесь х изменяется от 0 до а, следовательно, t изменяется от ПИ/2 до 0 (см. рис. 179). Находим:

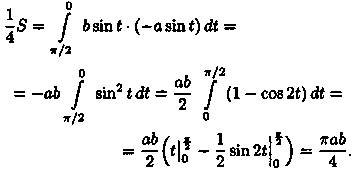
Таким образом 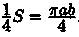. Значит, S = πаВ.

Полярные координаты

Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ — полярные координаты (см. рис. 180). Для решения задачи используем схему II — метод дифференциала.

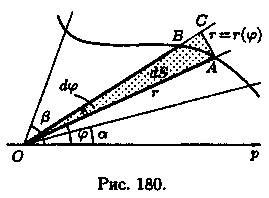
1. Будем считать часть искомой площади S как функцию угла φ, т. е. S = S(φ), где а ≤φ≤β (если φ = а, то S(a) = 0, если φ=β, то S(β) = S).

2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.

Дифференциал dS представляет собой главную часть приращения ΔS при dφ→0 и равен площади кругового сектора О АС (на рисунке она заштрихована) радиуса r с центральным углом dφ. Поэтому

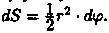
3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь

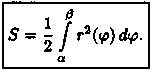
Пример 41.3. Найти площадь фигуры, ограниченной «трехлепесткoвой розой» r=acos3φ (см. рис. 181).

Решение: Найдем сначала площадь половины одного лепестка «розы», т. е.1/6часть всей площади фигуры:

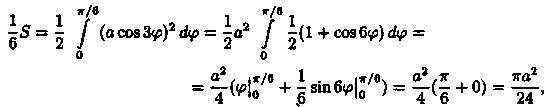
т. е. 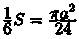. Следовательно,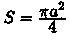

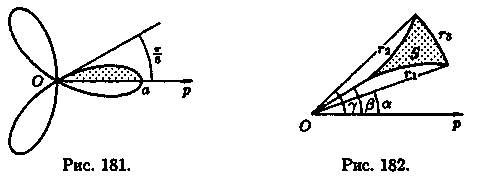
Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке 182, имеем: