Второй замечательный предел
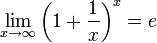 или
или 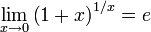
Доказательство второго замечательного предела:
Доказательство для натуральных значений x
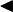 Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел длявещественных x, то есть докажем, что
Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел длявещественных x, то есть докажем, что  . Рассмотрим два случая:
. Рассмотрим два случая:
1. Пусть 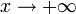 . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами: 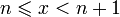 , где
, где 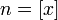 — это целая часть x.
— это целая часть x.
Отсюда следует: 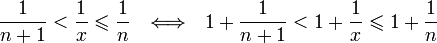 , поэтому
, поэтому
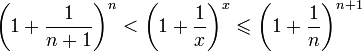 .
.
Если 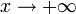 , то
, то 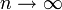 . Поэтому, согласно пределу
. Поэтому, согласно пределу 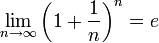 , имеем:
, имеем:
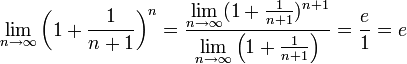
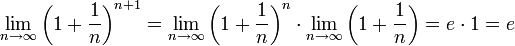 .
.
По признаку (о пределе промежуточной функции) существования пределов 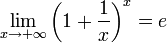 .
.
2. Пусть 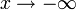 . Сделаем подстановку
. Сделаем подстановку 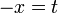 , тогда
, тогда 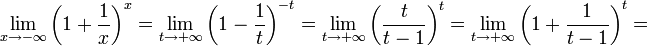
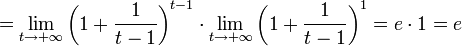 .
.
Из двух этих случаев вытекает, что 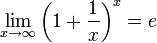 для вещественного x.
для вещественного x. 
Следствия
1. 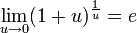
2. 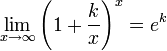
3. 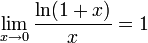
4. 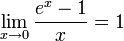
5. 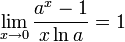 для
для 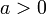 ,
, 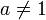
6. 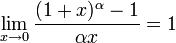
15. Предел суммы , разности, произведения и отношения функции.
Обозначение предела Предел функции обозначается как 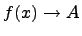 , при
, при 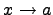 или через символ предела
или через символ предела 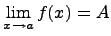 .
.
Всюду ниже предполагается, что пределы функций существуют.
Рассмотрим основные свойства пределов.
1. Предел суммы
Предел суммы равен сумме пределов, если каждый из них существует, т.е.
2. Предел разности
Предел разности равен разности пределов, если каждый из них существует, т.е. 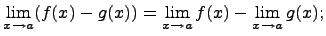
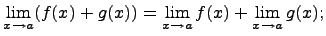
1. Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
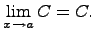
2. Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
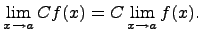
3. Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.
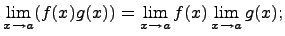
16. Асимптоты вертикальные, наклонные, горизонтальные, вычисление коэфицентов, графическая иллюзия.
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

Непрерывность функции в точке и на отрезке. Пределы сложной функции. Классификация точек разрыва.
Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точкех0, если предел функции и ее значение в этой точке равны, т.е. 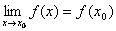
Тот же факт можно записать иначе: 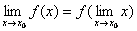
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию
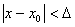 верно неравенство
верно неравенство 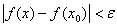 .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной. f(x) = f(x0) + a(x) где a(х) – бесконечно малая при х®х0.
