Линейная зависимость и независимость векторов
Опр.2. Вектор 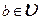 называется линейной комбинацией векторов
называется линейной комбинацией векторов 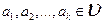 , если
, если 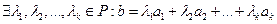 .
.
Говорят также, что вектор b линейно выражается через векторы 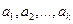 .
.
Опр.3. Система векторов 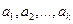 пространства
пространства  называется линейно зависимой, если существуют неравные нулю одновременно элементы
называется линейно зависимой, если существуют неравные нулю одновременно элементы 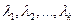 поля Р такие, что
поля Р такие, что 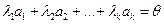 .
.
Опр.4. Система векторов 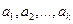 называется линейно независимой, если равенство
называется линейно независимой, если равенство 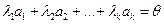 выполняется только при
выполняется только при 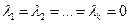 .
.
Свойства линейной зависимости векторов:
1) Система, содержащая нулевой вектор, линейно зависима.
Доказательство: Пусть первый вектор системы - нулевой, т.е. имеем систему 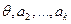 , тогда
, тогда 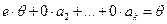 . То есть нашлись не равные нулю одновременно элементы поля Р -
. То есть нашлись не равные нулю одновременно элементы поля Р - 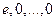 , такие что линейная комбинация системы векторов равна
, такие что линейная комбинация системы векторов равна 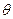 . Значит система векторов линейно зависима. ▲.
. Значит система векторов линейно зависима. ▲.
2) Система векторов линейно зависима, если какая-то её подсистема (часть) линейно зависима.
Доказательство: Пусть дана система векторов 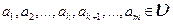 , причем её подсистема
, причем её подсистема 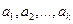 - линейно зависима. Значит, существуют не равные нулю одновременно
- линейно зависима. Значит, существуют не равные нулю одновременно 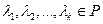 , такие, что
, такие, что 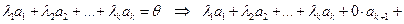
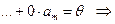 система
система 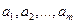 линейно зависима. ▲.
линейно зависима. ▲.
Следствие: любая подсистема линейно независимой системы векторов линейно независима.
3) Система векторов 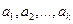 линейно зависима
линейно зависима 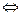 хотя бы одни вектор этой системы линейно выражается через остальные векторы системы.
хотя бы одни вектор этой системы линейно выражается через остальные векторы системы.
Доказательство: 1. 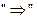 . Пусть
. Пусть 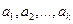 - линейно зависимая система
- линейно зависимая система 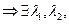
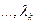 , не равные нулю одновременно, такие, что
, не равные нулю одновременно, такие, что 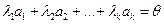 . Пусть для определенности
. Пусть для определенности 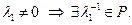 Тогда, умножив равенство на
Тогда, умножив равенство на 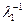 , получим:
, получим:
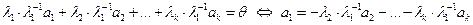 , т.е.
, т.е. 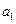 линейно выражается через
линейно выражается через 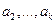 .
.
2. 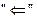 . Пусть, например,
. Пусть, например, 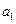 линейно выражается через
линейно выражается через 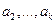
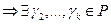 такие, что
такие, что 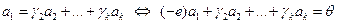 . Т.е. нашлись такие не равные нулю одновременно элементы поля Р:
. Т.е. нашлись такие не равные нулю одновременно элементы поля Р: 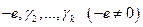 , что
, что 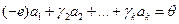 . Значит система векторов линейно зависима. ▲.
. Значит система векторов линейно зависима. ▲.
4) Если система векторов 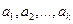 линейно независима, а система
линейно независима, а система 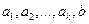 - линейно зависима, то вектор b единственным образом линейно выражается через
- линейно зависима, то вектор b единственным образом линейно выражается через 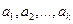 .
.
Доказательство: 1. Существование разложения. Так как система 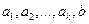 линейно зависима, то
линейно зависима, то 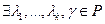 , не равные нулю одновременно, такие, что
, не равные нулю одновременно, такие, что 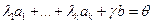 . Обязательно
. Обязательно 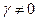 , т.к. в противном случае
, т.к. в противном случае 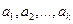 была бы линейно зависима. Значит
была бы линейно зависима. Значит 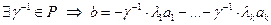 , то есть b линейно выражается через
, то есть b линейно выражается через 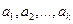 .
.
2. Единственность. Пусть вектор b может быть линейно выражен через вектора 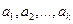 двумя способами. Т.е.
двумя способами. Т.е. 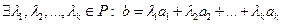 и
и 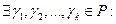
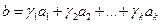 . Вычтем из первого равенства второе, получим:
. Вычтем из первого равенства второе, получим:
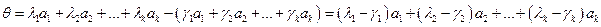
Так как система векторов 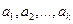 линейно независима, то такое равенство выполняется только при
линейно независима, то такое равенство выполняется только при 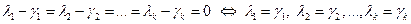 . То есть разложение вектора b по векторам
. То есть разложение вектора b по векторам 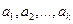 единственное. ▲.
единственное. ▲.
5) Пусть даны две системы векторов пространства  :
: 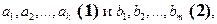 причем
причем 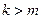 и каждый вектор системы
и каждый вектор системы 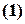 линейно выражается через векторы системы
линейно выражается через векторы системы 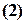 ,
,
тогда система 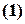 - линейно зависима.
- линейно зависима.
Доказательство: По условию, 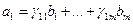
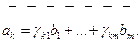
Система 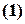 линейно зависима
линейно зависима 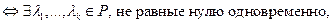
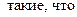
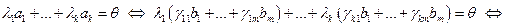
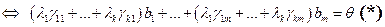
Рассмотрим систему уравнений: 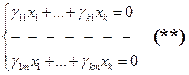
В этой однородной системе 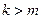 , т.е. число неизвестных больше, чем число уравнений системы, значит система имеет ненулевое решение.
, т.е. число неизвестных больше, чем число уравнений системы, значит система имеет ненулевое решение.
А значит и система 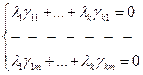 имеет ненулевое решение
имеет ненулевое решение 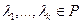
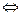 имеет место равенство
имеет место равенство 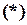
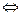 система
система 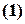 линейно зависима. ▲.
линейно зависима. ▲.
Примеры векторных пространств:
1. 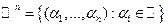 - арифметическое векторное пространство над
- арифметическое векторное пространство над 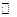 .
.
2. 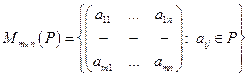 - множество всех матриц размера
- множество всех матриц размера 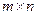 с элементами поля Р - векторное пространство над полем Р.
с элементами поля Р - векторное пространство над полем Р.
3. Многочлены от одной переменной с коэффициентами из поля Р - векторное пространство над Р - 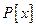 .
.
4. 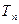 - многочлены от одной переменной с коэффициентами из поля Р степени не выше п.
- многочлены от одной переменной с коэффициентами из поля Р степени не выше п.
5.  - множество всех отображений множества
- множество всех отображений множества 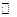 в
в 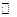 - векторное пространство над полем
- векторное пространство над полем 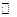 относительно операций сложения отображений и умножения отображений на действительные числа.
относительно операций сложения отображений и умножения отображений на действительные числа.
6. Множество 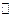 всех комплексных чисел есть векторное пространство над полем действительных чисел
всех комплексных чисел есть векторное пространство над полем действительных чисел 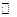 .
.
ВОПРОС № 5 Конечномерные векторные пространства. Базис и размерность. Координаты вектора.
 Опр.1. Пусть
Опр.1. Пусть  - векторное пространство над полем Р. Совокупность векторов
- векторное пространство над полем Р. Совокупность векторов 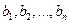 пространства
пространства  называется базисом пространства , если:
называется базисом пространства , если:
1) 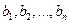 - линейно независимая система векторов;
- линейно независимая система векторов;
2) любой вектор пространства  линейно выражается через векторы
линейно выражается через векторы 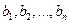 , т.е.
, т.е. 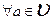
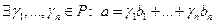 .
.
Теорема 1. Если пространство  над полем Р имеет базис, то любые 2 базиса пространства
над полем Р имеет базис, то любые 2 базиса пространства  содержат одинаковое число векторов.
содержат одинаковое число векторов.
Доказательство: Пусть 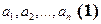 и
и 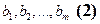 - 2 базиса пространства
- 2 базиса пространства  . Допустим, что
. Допустим, что 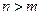 , тогда имеем: каждый вектор системы (1) линейно выражается через векторы системы (2), т.к. (2) - базис. А тогда, по свойствам линейной зависимости, имеем, что (1) - линейно зависима, что противоречит тому, что (1) - базис
, тогда имеем: каждый вектор системы (1) линейно выражается через векторы системы (2), т.к. (2) - базис. А тогда, по свойствам линейной зависимости, имеем, что (1) - линейно зависима, что противоречит тому, что (1) - базис  . Значит
. Значит 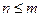 .
.
Аналогичное противоречие получим, если допустим, что 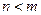 , значит
, значит 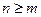 .
.
Итак, 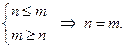 ▲.
▲.
Теорема 2. Если пространство  имеет базис, состоящий из п векторов, то любая линейно независимая система, содержащая п векторов, также образует базис пространства
имеет базис, состоящий из п векторов, то любая линейно независимая система, содержащая п векторов, также образует базис пространства  .
.
Доказательство: Пусть 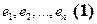 - базис пространства
- базис пространства  , а
, а 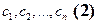 - произвольная линейно независимая система векторов. Покажем, что система (2) - базис
- произвольная линейно независимая система векторов. Покажем, что система (2) - базис  . Для этого надо показать, что (2) удовлетворяет второму условию определения базиса, т.е. что любой вектор пространства
. Для этого надо показать, что (2) удовлетворяет второму условию определения базиса, т.е. что любой вектор пространства  линейно выражается через векторы системы (2).
линейно выражается через векторы системы (2).
Пусть 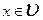 , добавим его к системе (2), получим систему
, добавим его к системе (2), получим систему 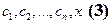 . Так как (1) - базис
. Так как (1) - базис  , то любой вектор пространства
, то любой вектор пространства  , а значит любой вектор системы (3) линейно выражается через вектора системы (1), а тогда
, а значит любой вектор системы (3) линейно выражается через вектора системы (1), а тогда 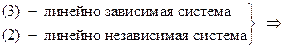 х линейно выражается через векторы системы (2). ▲.
х линейно выражается через векторы системы (2). ▲.
 Опр.2. Если пространство
Опр.2. Если пространство  имеет базис, то
имеет базис, то  называется конечномерным, а число векторов в любом базисе называется размерностью пространства и обозначается
называется конечномерным, а число векторов в любом базисе называется размерностью пространства и обозначается 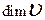 . В противном случае
. В противном случае  называется бесконечномерным. Если
называется бесконечномерным. Если  - конечномерное и
- конечномерное и 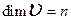 , то
, то  называют также п-мерным векторным пространством.
называют также п-мерным векторным пространством.
В п-мерном векторном пространстве  любая система векторов, содержащая более чем п векторов, линейно зависима. А в бесконечномерном векторном пространстве можно найти систему из любого числа линейно независимых векторов.
любая система векторов, содержащая более чем п векторов, линейно зависима. А в бесконечномерном векторном пространстве можно найти систему из любого числа линейно независимых векторов.
Примеры:
1. 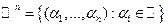 - п-мерное пространство. Базис -
- п-мерное пространство. Базис - 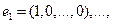
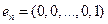 .
.
2.  - пространство матриц размера
- пространство матриц размера  над полем Р - конечномерное пространство, размерность
над полем Р - конечномерное пространство, размерность 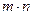 , базисом, например, будут векторы
, базисом, например, будут векторы 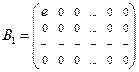 ,
, 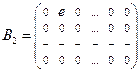 ,…,
,…, 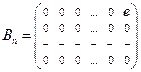 ,
, 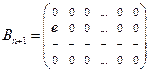 ,…,
,…, 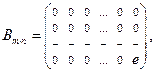 где е - единичный элемент поля Р.
где е - единичный элемент поля Р.
3. 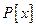 - пространство многочленов от одной переменной х над полем Р, бесконечномерно, т.к.
- пространство многочленов от одной переменной х над полем Р, бесконечномерно, т.к. 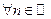 можно найти линейно независимую систему векторов, состоящую из п векторов -
можно найти линейно независимую систему векторов, состоящую из п векторов - 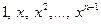 .
.
4. 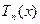 - пространство многочленов от одной переменной х над полем Р степени не выше п;
- пространство многочленов от одной переменной х над полем Р степени не выше п; 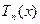 конечномерно, размерности
конечномерно, размерности 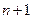 . Базис, например,
. Базис, например, 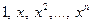 .
.
5. Множество 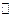 всех комплексных чисел есть векторное пространство над полем действительных чисел
всех комплексных чисел есть векторное пространство над полем действительных чисел 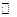 размерности 2; базис, например,
размерности 2; базис, например, 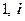 .
.
6. Любое поле Р есть векторное пространство над самим собой размерности 1; базис, например, единица е поля Р.
Координаты вектора
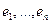 Опр.3. Пусть
Опр.3. Пусть  - п-мерное векторное пространство над полем Р;
- п-мерное векторное пространство над полем Р; 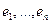 - базис
- базис 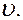 Тогда
Тогда 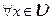
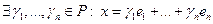 . Коэффициенты этого разложения
. Коэффициенты этого разложения 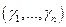 называют координатами вектора х в базисе .
называют координатами вектора х в базисе .
Легко показать, что справедливо следующее предложение:
Предложение: Координаты любого вектора в данном базисе конечномерного векторного пространства  определяются однозначно.
определяются однозначно.
Доказательство: Допустим, что некоторый вектор х пространства  имеет 2 разложения по базисным векторам
имеет 2 разложения по базисным векторам 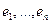 :
:
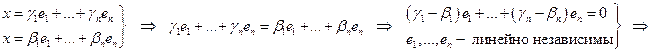
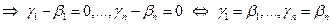 . Т.е. разложение единственно. ▲.
. Т.е. разложение единственно. ▲.
