Несобственные интегралы с бесконечными пределами интегрирования. Критерии сходимости несобственных интегралов

Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].

Определение: Если существует конечный предел 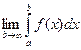, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).

Обозначение: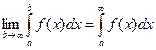

Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

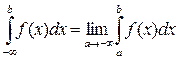
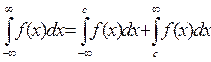
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Теорема: Если для всех х (x ³ a) выполняется условие 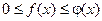и интеграл 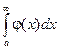сходится, то 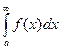тоже сходится и 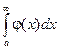³ .

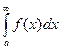Теорема: Если для всех х (x ³ a) выполняется условие 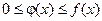и интеграл 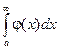расходится, то 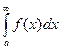тоже расходится.

Теорема: Если 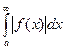сходится, то сходится и интеграл .

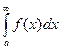В этом случае интеграл 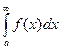называется абсолютно сходящимся.

19.Несобственные интегралы от неограниченных функций. Критерии сходимости несобственных интегралов
Интеграл от разрывной функции.

Если в точке х = с функция либо неопределена, либо разрывна, то

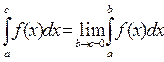
Если интеграл 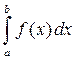существует, то интеграл 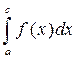- сходится, если интеграл 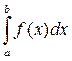не существует, то 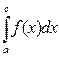- расходится.

Если в точке х = а функция терпит разрыв, то .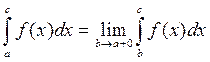

Если функция f(x) имеет разрыв в точке b на промежутке [a, с], то

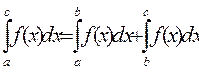
Таких точек внутри отрезка может быть несколько.

Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.

20.Приложения определенных интегралов к решению задач геометрии (вычисление площадей плоских фигур, поверхностей тел вращения, длины дуги кривой, объема тела вращения.
Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур.

У

+ +

0 a - b x

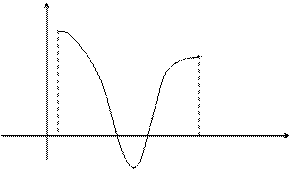
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

Для нахождения суммарной площади используется формула .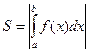

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.

Нахождение площади криволинейного сектора.

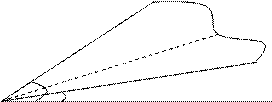r = f(j)

b

a

О r

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид r = f(j), где r - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а j - угол наклона этого радиус – вектора к полярной оси.

Площадь криволинейного сектора может быть найдена по формуле

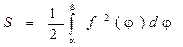
Вычисление длины дуги кривой.

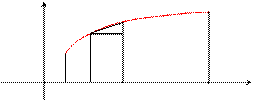y y = f(x)

DS_i Dy_i

Dx_i

a b x

Длина ломаной линии, которая соответствует дуге, может быть найдена как .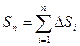

Тогда длина дуги равна .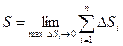

Из геометрических соображений: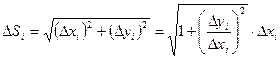

В то же время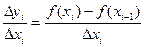

Тогда можно показать (см. Интегрируемая функция.), что

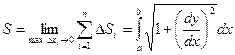
Т.е.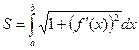

Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная фунции, заданной параметрически.), получаем

,

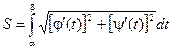где х = j(t) и у = y(t).

Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то

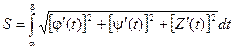
Если кривая задана в полярных координатах, то

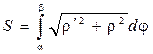, r = f(j).

Вычисление объемов тел.

Вычисление объема тела по известным площадям его параллельных сечений

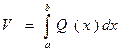
Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.

Объем тел вращения.

Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения. y = f(x)

:

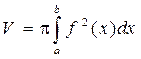
Площадь поверхности тела вращения.

Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.

Тогда 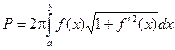- формула вычисления площади поверхности тела вращения.