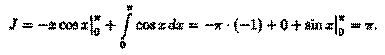Геометрический смысл несобственных интегралов с бесконечным пределом интегрирования

Несобственным интегралам можно придать смысл площади бесконечной фигуры.
Пример 1. Вычислить .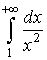
Решение. По определению имеем

.

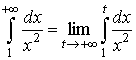Для нахождения интеграла, стоящего под знаком предела, воспользуемся формулой Ньютона-Лейбница

.

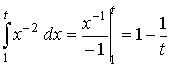Тогда

,

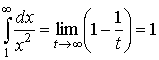т.е. искомый несобственный интеграл сходится к 1.
Аналогично, можно убедиться, что интеграл

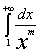
сходится к 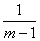, если m > 1, и расходящимся, если m ≤ 1.
Геометрический смысл этого результата состоит в том, что среди всех кривых вида 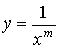гипербола 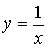является своеобразным "порогом". Если кривая данного вида на интервале [1; + ∞) лежит ниже гиперболы, то полубесконечная фигура имеет конечную площадь. Если же кривая лежит выше или совпадает с гиперболой 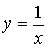, то соответствующая фигура имеет бесконечную площадь.

Пример 2. Вычислить .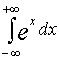
Решение. Исследуем на сходимость интегралы 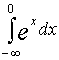и :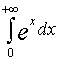

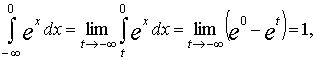
т.е. первый из интегралов сходится к 1. Но

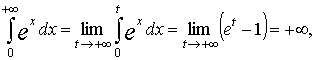
т.е. этот интеграл расходится и, следовательно, расходится несобственный интеграл .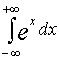

ВОПРОС 68. Формула Ньютона-Лейбница. Интегралы по симметричным промежуткам от чётных и нечётных функций. Оценки интегралов. Интегрально среднее.

Простым и удобным методом вычисления определенного интеграла 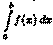от непрерывной функции является формула Ньютона-Лейбница:

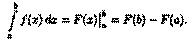
Применяется этот метод во всех случаях, когда может быть найдена первообразная функции F(x) для подынтегральной функции ƒ (х).

Например,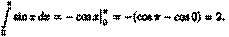

При вычисленииопределенных интегралов широко используется метод замены переменной и метод интегрирования по частям.

39.2. Интегрирование подстановкой (заменой переменной)

Пусть для вычисления интеграла 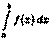от непрерывной функции

сделана подстановка х = φ(t).

Теорема 39.1. Если:

1) функция х = φ(t) и ее производная х' = φ'(t) непрерывны при t є [а;β];

2) множеством значений функции х = φ(t) при t є [а,β] является отрезок [а; b];

3) φ(а)=а и φ(β)=b.

то

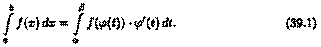
▼Пусть F(x) есть первообразная для ƒ(х) на отрезке [а;b]. Тогда по формуле Ньютона-Лейбница 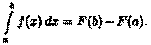Так как (F(φ(t))' = f(φ(t)) - φ'(t), то F(φ(t)) является первообразной для функции f(φ(t)) -φ'(t), t  [а;β]. Поэтому по формуле Ньютона—Лейбница имеем

▲

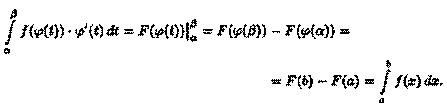Формула (39.1) называется формулой замены переменной в определенном интеграле. Отметим, что:

1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;

2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x);

3) не следует забывать менять пределы интегрирования при замене переменных!

Пример 39.1. Вычислить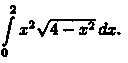

Решение: Положим х = 2 sin t, тогда dx = 2 cos t dt. Если х=0, то t = 0; если x = 2, то t = 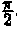. Поэтому

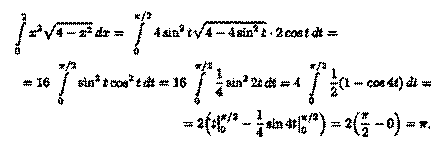
39.3. Интегрирование по частям

Теорема 39.2. Если функции u = u(х) и v = v(x) имеют непрерывные производные на отрезке [а; b], то имеет место формула

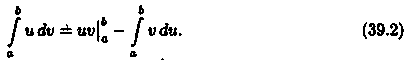
▼На отрезке [а; b] имеет место равенство (uv)' = u'v+uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v+uv'. Тогда по формуле Ньютона-Лейбница имеем:

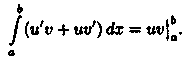
Следовательно,

▲

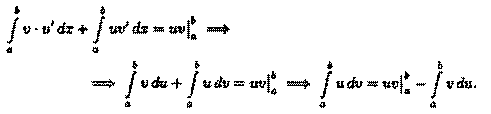Формула (39.2) называется формулой интегрирования по частям для определенного интеграла.

Пример 39.2. Вычислить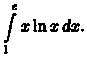

Решение: Положим

Применяя формулу (39.2), получаем

Пример 39.3. Вычислить интеграл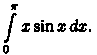

Решение: Интегрируем по частям. Положим

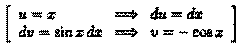
Поэтому