Основные понятия и определения

Теория теплообмена изучает процессы распространения теплоты в твердых, жидких и газообразных телах. Перенос теплоты может передаваться тремя способами:

– теплопроводностью;

– конвекцией;

– излучением (радиацией).

Процесс передачи теплоты теплопроводностью происходит при непосредственном контакте тел или частицами одного тела с различными температурами и представляет собой молекулярный процесс передачи теплоты. При нагревании тела кинетическая энергия его молекул возрастает и частицы более нагретой части тела, сталкиваясь с соседними молекулами, сообщают им часть своей кинетической энергии.

Конвекция – это перенос теплоты при перемещении и перемешивании всей массы неравномерно нагретых макрочастиц жидкости или газа. При этом перенос теплоты зависит от скорости движения жидкости или газа прямо пропорционально. Этот вид передачи теплоты сопровождается всегда теплопроводностью. Одновременный перенос теплоты конвекцией и теплопроводностью называется конвективным теплообменом.

В инженерных расчетах часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей, а процесс переноса теплоты от одной жидкой среды к другой через разделяющую их твердую стенку – теплопередачей.

Процесс передачи теплоты внутренней энергии тела в виде электромагнитных волн называется тепловым излучением (радиацией). Совместный теплообмен излучением и теплопроводностью называют радиационно-кондуктивным теплообменом.

Совокупность всех трех видов теплообмена называется сложным теплообменом.

Процессы теплообмена могут происходить в различных средах – твердых телах, жидкостях, газах и разных смесях, при изменении и без изменения агрегатного состояния рабочих сред и т. д. В зависимости от этого теплообмен протекает по-разному и описывается различными уравнениями.

В первой части курса по тепломассообмену для студентов ИЭФ рассматривается передача тепла теплопроводностью. Решение задач теплопроводности проводится для однородных и изотропных тел, т. е. таких тел, которые обладают одинаковыми физическими свойствами по всем направлениям. При передаче теплоты в твердом теле, температура тела будет изменяться как в пространстве, так и во времени.

Совокупность значений температуры в данный момент времени для всех точек пространства называется температурным полем:

.

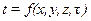Такое температурное поле называется нестационарным, т. е. соответствует неустановившемуся тепловому режиму теплопроводности. Если температура тела является функцией только координат и не изменяется с течением времени, то температурное поле называется стационарным:

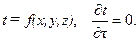
Изотермической поверхностью называется поверхность тела с одинаковой температурой.

Градиент температуры – это вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры по нормали:

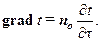
Количество теплоты, проходящее через изотермическую поверхность F в единицу времени, называется тепловым потоком – Q, [Вт=Дж/с].

Тепловой поток, проходящий через единицу площади называют плотностью теплового потока – 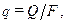[Вт/м²].

Для твердого тела уравнение теплопроводности подчиняется закону Фурье: Тепловой поток, передаваемый теплопроводностью, пропорционален градиенту температуры и площади сечения перпендикулярного направлению теплового потока.

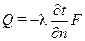или

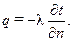
Коэффициент теплопроводности λ является физическим параметром вещества, характеризующим способность тела проводить теплоту.

Дифференциальное уравнение теплопроводности для трехмерного нестационарного температурного поля при условии, что внутренние источники тепла отсутствуют, можно записать как

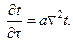
Коэффициент температуропроводности а зависит от рода вещества, давления и температуры. Для большинства веществ он определяется опытным путем, и для технических расчетов его значение берут из справочной литературы.

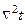– оператор Лапласа.

В прямоугольной декартовой системе координат (x,y,z) он записывается в виде

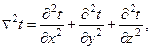
а в цилиндрической (z, r, j) –

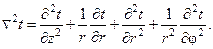
При решении задач нестационарной теплопроводности используются два безразмерных комплекса:

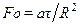– число Фурье (характеризует безразмерное время).

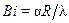– число Био (характеризует отношение внутреннего термического сопротивления 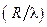, обусловленного теплопроводностью, к внешнему термическому сопротивлению 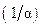, обусловленному конвекцией.

КОНТРОЛЬНЫЕ ЗАДАНИЯ

Задача 1

Определение количества тепла, проходящего через

плоскую стенку при граничных условиях I рода

Определить количество теплоты Q, проходящее через плоскую стенку, выложенную из красного кирпича. Длина стенки L, м, высота h, м, толщина соответствует 2,5 длины стандартного кирпича. Одна из поверхностей оштукатурена слоем d. На поверхностях стены поддерживаются температуры t_c1 и t_c2. Коэффициент теплопроводности кирпичной кладки l = 0,75 Вт/(м ^оС), коэффициент теплопроводности штукатурки l = 1,2 Вт/(м ^оС).

Таблица 1

Первая цифра варианта
L, м				2,5	3,5	4,5		5,5
h, м	3,3	2,5		2,3		2,7		2,5		3,3
d, мм
Последняя цифра варианта
t c1, оС
t c2, оС					–3		–8

Решить задачу и ответить письменно на следующие вопросы:

1. Какие параметры задачи изменятся и почему, если слои поменять местами?

2. Как передается теплота в процессе теплопроводности? Сформулируйте основной закон теплопроводности.

3. Что такое тепловой поток, плотность теплового потока, температурное поле?

4. Каков закон распределения температуры по толщине плоской многослойной стенки?

5. Физический смысл коэффициента теплопроводности λ и его размерность.

Задача 2

Определение мощности электронагревателя для

обогрева помещения

Помещение с внутренними габаритами 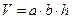, где а – длина, b – ширина, h – высота, выполнено из панелей толщиной d. Материал панелей имеет коэффициент теплопроводности l. Какой мощности электронагреватель нужно установить, чтобы температура в помещении сохранялась на

уровне t_вн, если температура наружного воздуха t_н, а коэффициенты теплоотдачи соответственно на внутренних и внешних поверхностях панелей следующие:

a_c1 = 9 Вт/(м²∙^оС), a_с2 = 20 Вт/(м²∙^оС) (для стен);

a_п1 = 10 Вт/(м²∙^оС), a_п2 = 4 Вт/(м²∙^оС) (для пола);

a_пт1 = 8Вт/(м²∙^оС), a_пт2 = 15 Вт/(м²∙^оС) (для потолка).

Таблица 2

Первая цифра варианта
а, м		3,5		3,3					2,5
b, м					2,5				5,5
h, м	2,5		2,5	3,3			5,5		6,6
d, м	0,5	0,3	0,75	0,225	0,33	0,7	0,35	0,45	0,5	0,15
Последняя цифра варианта
l, Вт/(м оС)	0,09	0,1	0,41	0,58	0,47	0,7	0,35	0,52	0,15	1,69
tвн, оС
tн, оС	–5	–10	–35	–30	–25	–15	–10	–30	–6	–15

Решить задачу и ответить письменно на следующие вопросы:

1. В чем отличие между теплопроводностью, конвективным теплообменом и излучением?

2. Какова математическая запись закона Фурье и закона Ньютона – Рихмана?

3. Физический смысл коэффициента теплоотдачи α и его размерность?

4. Что такое термическое сопротивление? Какова размерность величины термического сопротивления?

5. В чем отличие между термическими сопротивлениями теплоотдачи на поверхности плоской стенки и термическими сопротивлениями теплопроводности плоской стенки?

Задача 3

Расчет параметров изолированного трубопровода

По трубопроводу с размерами 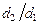, где d₁ – внутренний диаметр трубы, а d₂ – наружный диаметр, течет горячая вода с температурой t_ж1. Температура окружающей среды t_ж2. Снаружи труба покрыта слоем изоляционного материала толщиной d с коэффициентом теплопроводности l₂, коэффициентом теплопроводности материала трубы l₁. Средние коэффициенты теплоотдачи с внутренней поверхности трубы и внешней изоляционного материала соответственно равны a₁, a₂. Определить количество теплоты, отдаваемой единицей длины трубы в окружающее пространство, а также температуры на внутренней и внешней поверхностях трубы.

Таблица 3

Первая цифра варианта
d1, мм		24,45	24,3	30,7	39,5			30,7		24,4
d2, мм		26,8	26,8	33,5	42,3			33,5		26,8
d, мм
Последняя цифра варианта
tж1, оС					100,5		98,8
tж2, оС
l1, Вт/(м∙оС)
l2, Вт/(м∙оС)	0,06	0,038	0,041	0,052	0,064	0,07	0,056	0,04	0,084	0,05
a1, Вт/(м2∙оС)
a2, Вт/(м2∙оС)

Решить задачу и ответить письменно на следующие вопросы:

1. В чем отличие между коэффициентами теплопроводности, теплоотдачи, температуропроводности и теплопередачи? Какова их размерность, каков их физический смысл?

2. Какому закону соответствует распределение температуры в цилиндрической однослойной стенке?

3. Каким образом определяются тепловые потери с цилиндрической поверхности однослойной теплоизоляции при граничных условиях I рода?

4. Как определяется коэффициент теплопередачи для многослойной цилиндрической стенки при граничных условиях III рода?

5. Какова зависимость тепловых потерь трубопровода от наружного диаметра его теплоизоляции, если: а) критический диаметр теплоизоляции меньше наружного диаметра стальной трубы; б) критический диаметр теплоизоляции больше наружного диаметра стальной трубы?

Задача 4

Определение количества тепла, отдаваемого

радиатором отопления

Нагревательный прибор, выполненный в виде стальной цилиндрической трубы с оребренной поверхностью, имеет следующие характеристики: внутренний и наружный радиусы ребер постоянной толщины d соответственно равны r₁ и r₂, коэффициент теплоотдачи от поверхности ребра a_р, коэффициент теплоотдачи от неоребренной поверхности a_п, коэффициент теплопроводности стали l=50 Вт/(м^оС), температура в основании ребра t₁. Определить количество теплоты_, отдаваемое всем прибором в окружающую среду с температурой t_ж1, если длина прибора ℓ, а количество ребер n.

Таблица 4

Первая цифра варианта
r1, мм			26,8	33,5	42,3			21,3		13,5
r2, мм
d, мм			3,5		2,5		3,5
l, мм
Последняя цифра варианта
aр, Вт/(м2∙оС)	9,3	9,3	46,5		23,3		8,7	9,9	46,5	23,3
aп , Вт/(м2∙оС)		9,3	23,5						23,3	23,3
t1 оС								99,9
tж1, оС
n, шт.

Решить задачу и ответить письменно на следующие вопросы:

1. Напишите дифференциальное уравнение стационарной теплопроводности в декартовой и цилиндрической системах. Каков физический смысл дифференциального уравнения теплопроводности?

2. Какие из перечисленных величин, характеризующих передачу теплоты через наружную поверхность цилиндра, не зависят от его диаметра: тепловой поток, поверхностная плотность теплового потока, линейная плотность теплового потока?

3. Какие условия должны быть определены (или заданы) для однозначного решения дифференциального уравнения теплопроводности?

4. Каким образом можно интенсифицировать процесс теплопередачи?

5. Как оребрение влияет на теплопередачу?

Задача 5

Определение времени нагревания вала до заданной температуры

Длинный стальной вал диаметром d = 2r_0, который имел температуру t₀, ^оС, был помещен в печь с температурой t_ж, ^оС. Определить время t, необходимое для нагрева вала, если нагрев считается законченным, когда температура на оси вала станет равной t _r=0 ^оC. Определить также температуру на поверхности вала t _r=r0 в конце нагрева.

Коэффициент теплопроводности и температуропроводности стали равны соответственно l и а. Коэффициент теплоотдачи к поверхности вала a. Для решения воспользоваться номограммами (прил. 3, 4).

Таблица 5

Первая цифра варианта
t0 оС
tж, оС
t r=0, оС
r0, мм
Последняя цифра варианта
l, Вт/(м оС)				45,4	45,5				37,2
а 10-5, м2/с	6,11	3,95	4,57	6,42	1,75	12,5	0,64	4,47	7,72	6,55
a, Вт/(м2∙оС)

Решить задачу и ответить письменно на следующие вопросы:

1. Чем нестационарное температурное поле отличается от стационарного?

2. Как записывается одномерное уравнение теплопроводности в декартовой и цилиндрической системах координат для нестационарного случая при условии, что внутренние источники тепла отсутствуют?

3. Какие методы используются для решения нестационарного уравнения теплопроводности?

4. Как определяется критерий Био и что характеризует?

5. Каким образом определяется относительная температура при решении задач нестационарной теплопроводности?

Задача 6

Определение количества тепла, отдаваемого валом и

температуры на его оси и поверхности при заданном времени охлаждения

Цилиндр диаметром d охлаждается в среде, имеющей постоянную температуру t_ж. В начальный момент времени температура цилиндра всюду была одинакова t₀. Коэффициент теплоотдачи во всех точках поверхности цилиндра в процессе охлаждения оставался постоянным и равным a.

Коэффициенты теплопроводности, температуропроводности и плотность материала соответственно равны l, а, r.

Определить количество тепла, которое будет отдано 1 пог. м цилиндра окружающей среде, и температуры на его оси и поверхности в течение 45 минут после начала охлаждения. Для решения воспользоваться соответствующими номограммами (прил. 3, 4).

Таблица 6

Первая цифра варианта
l, Вт/м К			14,4
а 10-5, м2/с	1,62	1,86	0,39	1,86	1,63	1,62	8,82	1,17	1,17	1,86
r, кг/м3
a , Вт/(м2∙оС)
Последняя цифра варианта
d, мм
l, м
t0 оС
tж оС

Решить задачу и ответить письменно на следующие вопросы:

1. Приведите практические примеры нестационарных тепловых процессов.

2. Какие условия ставятся при решении нестационарных задач теплопроводности и как они записываются?

3. Как определяется критерий Фурье и что данный критерий характеризует?

4.Как записываются граничные условия на оси симметрии и поверхности цилиндрического стержня при решении задачи о его нагревании или охлаждении?

5. Как коэффициент теплоотдачи α влияет на время нагревания или охлаждения твердых тел?

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1

Определение количества теплоты Q,

проходящее через двухслойную плоскую стенку

Определить количество теплоты Q, Вт, проходящее через плоскую стенку, выложенную из красного кирпича. Длина стенки L = 4,5 м, высота H = 2,7 м, толщина соответствует 2,5 длины стандартного кирпича (d_кр=0,640 мм). Одна из поверхностей оштукатурена слоем d_ш = 22 мм. На поверхностях стены поддерживается температура t_с1 =20°С и t_с3 = –25 °С. Коэффициент теплопроводности кирпичной кладки l_кр = 0,75 Вт/(м×°С), коэффициент теплопроводности штукатурки l_ш=1,2 Вт/(м×°С). Найти значение температуры на границе соприкосновения кирпичной кладки и штукатурки.

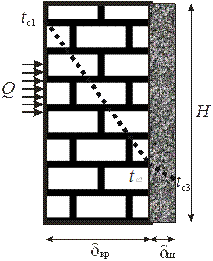
Рис. 1. Схема двухслойной плоской стенки

Решение.

Количество теплоты Q, проходящее через плоскую стенку в единицу времени, определяется по формуле

,

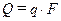где q – плотность теплового потока, Вт/м²; F – площадь поверхности, м².

Плотность теплового потока определим как

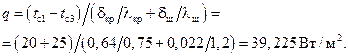
Вычислим площадь поверхности:

F=L·H=4,5·2,7=12,15 м².

Тогда количество теплоты будет равно

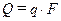=39,225·12,15=476,58 Вт.

Задача 2

Определение теплопотерь через ограждающую

конструкцию

Помещение с внутренними габаритами 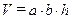, где а = 2,5 м – длина, b = 5,5 м – ширина, h = 6,6 м – высота, выполнено из панелей толщиной d = 0,7 м. Материал панелей имеет коэффициент теплопроводности l = 0,7 Вт/(м ×^oC).

Какой мощности электронагреватель нужно установить, чтобы температура в помещении сохранялась на уровне t_в = 19°С, если температура наружного воздуха t_н = –15 °С, а коэффициенты теплоотдачи соответственно на внутренних и внешних поверхностях панелей следующие:

a_c1=9 Вт/(м²×^оС), a _c2=20 Вт/(м²× ^оС) (для стен);

a _п1=10 Вт/(м²× ^оС ), a _п2=4 Вт/(м²× ^оС) (для пола);

a _пт1=8 Вт/(м²× ^оС ), a _пт2=15 Вт/(м²× ^оС) (для потолка).

Рис. 2. Габариты помещения

Решение.

Мощность электронагревателя должна быть такой, чтобы восполнять все теплопотери через ограждающие конструкции помещения:

.

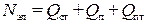Определим тепловые потери через ограждающие конструкции –

а) через стены:

– плотность теплового потока

= ;

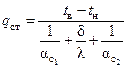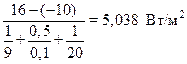– площадь четырех стен

F=2·h (a+b) = ;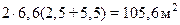

– количество теплоты

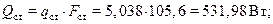
б) через пол:

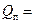
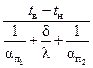(a∙b)= 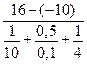(2,5∙5,5)=66,82 Вт;

в) через потолок:

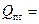
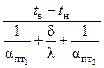(a∙b)= 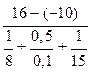(2,5∙5,5)=68,86 Вт.

Необходимая мощность электронагревателя составит

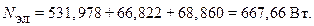
Задача 3

Расчет теплопередачи через цилиндрическую стенку

По трубопроводу с размерами 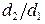, где d₁ –внутренний диаметр трубы, равный 20 мм, а d₂ – наружный диаметр, равный 22 мм, течет горячая вода с температурой t_ж1=95 °С. Температура окружающей среды t_ж2=22 °С.

Снаружи труба покрыта слоем изоляционного материала толщиной d=10 мм с коэффициентом теплопроводности l₂=0,07 Вт/(м∙ 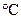), коэффициентом теплопроводности материала трубы l₁=211 Вт/(м∙ 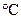). Средние коэффициенты теплоотдачи с внутренней поверхности трубы и внешней изоляционного материала соответственно равны a₁=100 Вт/(м²∙ 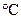) и a₂ = 5000 Вт/(м²∙ 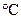). Определить количество теплоты, отдаваемой единицей длины трубы, в окружающее пространство, а также температуры на внутренней поверхности трубы и внешней поверхности изоляции.

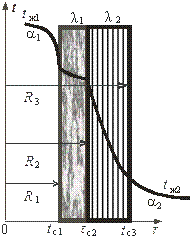
Рис. 3. Схема двухслойной цилиндрической стенки

Решение.

Найдем диаметр d₃ , определяющий внешнюю толщину трубы по формуле

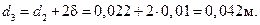
Линейную плотность теплового потока при теплопередаче через двухслойную цилиндрическую стенку определим по формуле

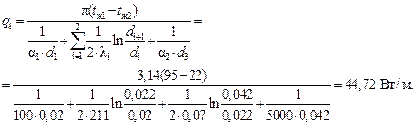
Количество теплоты, отдаваемой единицей длины трубы (l =1м) в окружающее пространство, найдем по формуле

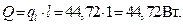
Температуру на внутренней поверхности стенки трубопровода определим по формуле

,

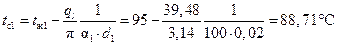а на внешней поверхности изоляции можно либо по формуле

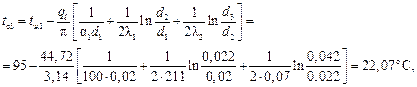
либо

.

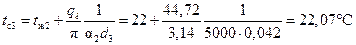Задача 4

Расчет теплопередачи через оребренную стенку

Нагревательный прибор, выполненный в виде стальной цилиндрической трубы с оребренной поверхностью, имеют следующие характеристики: внутренний и наружный радиусы ребер постоянной толщины d=3 мм и соответственно равны R₁=140 мм и R₂=220 мм, коэффициент теплоотдачи от поверхности ребра a_р=20 Вт/(м²∙ 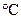), коэффициент теплоотдачи от неоребренной поверхности a_п =8 Вт/(м²∙ 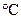), коэффициент теплопроводности стали l=50 Вт/(м∙ 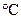), температура в основании ребра t₁=60°С.

Определить количество теплоты, отдаваемое всем прибором в окружающую среду с температурой t₀ = 5 °С, если длина прибора l = 500 мм, а количество ребер n = 25 шт. При решении задачи необходимо воспользоваться таблицами для определения значений функции Бесселя (прил. 1, 2).

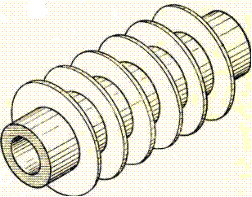
Рис. 4. Цилиндрическая труба с оребрением

tосн

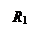
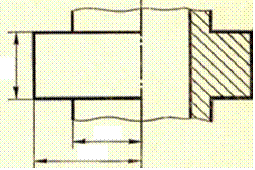
Рис. 5. Схема оребрения трубы

Решение.

Количество теплоты, отдаваемое поверхностью ребра в окружающую среду, будет равно количеству теплоты, подводимому к основанию ребра:

,

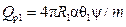m – определяется по формуле

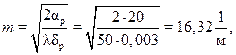
где a_р – коэффициент теплоотдачи от поверхности ребра, Вт/(м²×^oC);

l – теплопроводность материала трубы, Вт/ (м× ^oC);

d _р – толщина ребра, м.

Избыточная температура θ₁ стержня определяется как

Количество тепла, отдаваемое всеми ребрами:

.

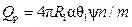Функция y определяется с учетом поправки на радиус R₂, которая учитывается как :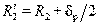

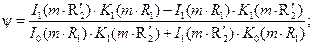
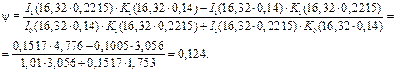
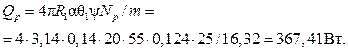
Количества тепла, отдаваемое гладкой поверхностью между ребрами:

,

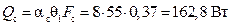где F_с – площадь поверхности неоребренной стенки определяется по формуле

F_с=2pR₁(l−nd_p)=2×3,14×0,14(0,500−25×0,003) = 0,37 м².

Теплота, отводимая от оребренной цилиндрической стенки в единицу времени, будет равна

Q=367,41+162,8=530,21 Вт.

Задача 5

Определение времени t, необходимое для нагрева вала, а также температуры на поверхности вала в конце нагрева

Длинный стальной вал диаметром d=120 мм, который имел температуру t₀=20 ºС, был помещен в печь с температурой t_ж=700 ºС. Определить время t, необходимое для нагрева вала, если нагрев считается законченным, когда температура на оси вала станет равной t_r=0=680 ºC. Определить также температуру на поверхности вала t_r=r0 в конце нагрева.

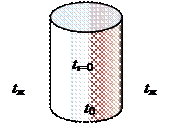Коэффициент теплопроводности и температуропроводности стали равны соответственно l=59 Вт/(м׺C) и а=1,626×10^-5 м²/с. Коэффициент теплоотдачи к поверхности вала a=160 (Вт/м²× ºC) .

Рис. 6. Нагревание вала

Решение.

Для определения температуры на оси и на поверхности цилиндра при нагревании (охлаждении) в среде с постоянной температурой воспользуемся графиком зависимости θ=F₁(Fо, Bi) (рис. 5) для оси цилиндра и графиком зависимости θ=F₂(Fо, Bi) (рис. 6) для поверхности цилиндра. Для этого необходимо определить число Bi, безразмерные температуры на оси цилиндра и на его поверхности по формулам:

Вi=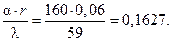

Безразмерную температуру на оси вала определим как:

,

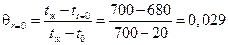где t_ж – температура окружающей вал среды; t_r=0 – температура на оси вала в конце нагрева; t₀ – температура на оси вала в начале нагрева.

По графику зависимости θ=F₁(Fо, Bi) (рис. 7 – прямая линия) для оси цилиндра определим число Фурье Fо, характеризующее безразмерное время Fо=11,7. Тогда время, необходимое для нагрева вала определится по формуле

,

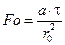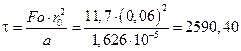с=43,17 мин.

Зная числа Фурье и Био, определим безразмерную температуру на поверхности цилиндра из графика зависимости θ=F₂(Fо, Bi) (рис. 8 – прямая линия) для поверхности цилидра θ _r=r0=0,028.

Рис. 7. Зависимость безразмерной температуры

на оси цилиндра от чисел Фурье и Био

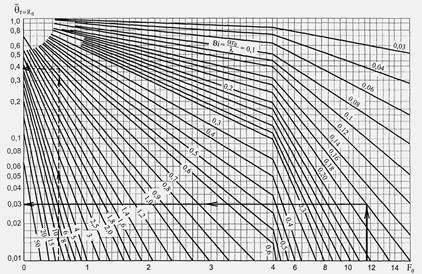
Рис. 8. Зависимость безразмерной температуры

на поверхности цилиндра от чисел Фурье и Био

Выразим температуру на поверхности цилиндра из формулы:

;

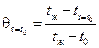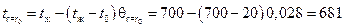^оС.

Задача 6

Охлаждение цилиндра

Цилиндр диаметром d=600 мм охлаждается в среде, имеющей постоянную температуру t_ж=5 °С. В начальный момент времени температура цилиндра всюду была одинакова t₀=600 °С. Коэффициент теплоотдачи во всех точках поверхности цилиндра в процессе охлаждения оставался постоянным и равным a=160 Вт/(м²×^оС).

Коэффициенты теплопроводности, температуропроводности и плотность материала соответственно равны

l=59 Вт/(м×^оС ), а=1,626×10^-5 м²/с, r=7849 кг/м³.

Определить количество тепла, которое будет отдано 1 погонным метром цилиндра окружающей среде в течение 45 минут (2700 сек.) после начала охлаждения.

Решение.

Найдем число Био и число Фурье:

Вi= ,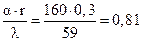

.

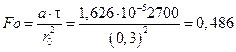Зная Bi и Fo, определим безразмерные температуры на оси цилиндра и на его поверхности: θ_r=0=0,61; θ_r=r0=0,39 (рис. 7, 8 – пунктирная линия).

Тогда температуры на оси цилиндра и на его поверхности определятся по формулам:

;

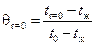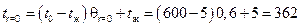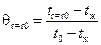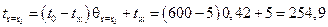^оС;

;

^оС.

Количество теплоты, отданное поверхностью цилиндра в окружающую среду, определим по формуле

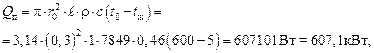
где с – теплоемкость металла, из которого выполнен трубопровод, кДж/(кг·^оС) (определяется по таблице теплофизических свойств металлов).

ПРИЛОЖЕНИЯ

Приложение 1

Модифицированные функции Бесселя первого рода

нулевого и первого порядков I₀(х) и I₁(x).

X	I0(х)	I1(x)	X	I0(х)	I1(x)
0,0	1,000	0,000	3,0	4,881	3,953
0,1	1,0025	0,0501	3,1	5,294	4,326
0,2	1,0100	0,1005	3,2	5,747	4,734
0,3	1,0226	0,1517	3,3	6,243	5,181
0,4	1,0404	0,2040	3,4	6,785	5,670
0,5	1,0635	0,2579	3,5	7,378	6,206
0,6	1,0920	0,3137	3,6	8,028	6,793
0,7	1,1263	0,3719	3,7	8,739	7,436
0,8	1,1665	0,4329	3,8	9,517	8,140
0,9	1,2130	0,4971	3,9	10,369	8,913
1,0	1,2661	0,5652	4,0	11,30	9,76
1,1	1,3262	0,6375	4,1	12,32	10,69
1,2	1,3937	0,7147	4,2	13,44	11,71
1,3	1,4693	0,7973	4,3	14,67	12,82
1,4	1,5534	0,8861	4,4	16,01	14,05
1,5	1,6467	0,9817	4,5	17,48	15,39
1,6	1,7500	1,0848	4.6	19,09	16,86
1,7	1,8640	1,1963	4,7	20,86	18,48
1,8	1,9896	1,3172	4,8	22,79	20,25
1,9	2,1277	1,4482	4,9	24,91	22,20
2,0	2,280	1,591	5,0	27,24	24,34
2,1	2,446	1,746	5,1	29,79	26,68
2,2	2,629	1,914	5,2	32,58	29,25
2,3	2,830	2,098	5,3	35,65	32,08
2,4	3,049	2,298	5,4	39,01	35,18
2,5	3,290	2,517	5,5	42,70	38,59
2,6	3,553	2,755	5,6	46,74	42,33
2,7	3,842	3,016	5,7	51,17	46,44
2,8	4,157	3,301	5,8	56,04	50,95
2,9	4,503	3,613	5,9	61,38	55,90

Приложение 2

Модифицированные функции Бесселя второго рода

нулевого и первого порядков K₀(х) и K₁(x).

X	K0(х)	K1(x)	X	K0(х)	K1(x)
0,0		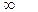	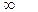2,2	0,089	0,108
0,1	2,447	9,854	2,3	0,078	0,0942
0,2	1,753	4,776	2,4	0,071	0,0832
0,3	1,373	3,056	2,5	0,062	0,0739
0,4	1,115	2,184	2,6	0,055	0,0660
0,5	0,924	1,656	2,7	0,049	0,0581
0,6	0,775	1,303	2,8	0,044	0,0503
0,7	0,661	1,050	2,9	0,039	0,0456
0,8	0,565	0,862	3,0	0,0347	0,0402
0,9	0,487	0,717	3,1	0,0314	0,0372
1,0	0,421	0,602	3,2	0,0283	0,0314
1,1	0,366	0,509	3,3	0,0251	0,0283
1,2	0,318	0,435	3,4	0,0220	0,0251
1,3	0,278	0,372	3,5	0,0196	0,0222
1,4	0,244	0,320	3,6	0,0173	0,0204
1,5	0,214	0,278	3.7	0,0157	0,0173
1,6	0,188	0,241	3,8	0,0141	0,0157
1,7	0,165	0,209	3,9	0,0126	0,0141
1,8	0,146	0,183	4,0	0,0112	0,0125
1,9	0,129	0,160	4,5	0,0064	0,0071
2,0	0,114	0,140	5,0	0,0037	0,0040
2,1	0,100	0,122

Приложение 3

Приложение 4

Приложение 5

Теплотехнические характеристики некоторых материалов

Материал	Плотность ρ, кг/м3	Теплоемкость с, кДж/(кг·оС)	Коэффициент теплопроводности λ, Вт/(м·оС )
Серебро		0.23
Медь		0.38
Золото		0.13
Алюминий		0.89
Серый чугун		0.54
Железо пудлинговое		0,46
Сталь		0,48
Железобетон		0,84	1,63
Вата х/б		0,042	–
Гипс		0,43	0,8–0,92
Глина	2000–1600	0,7–0,9	0,84
Гравий		0,36	–
Дерево	546–825	0,2–0,72	3,39–2,72
Кирпич	1700–1900	0,7–0,81	0,84–0,88
Пробка			~0,05
Стекловата		0,75	~0,05
Войлок строительный		1,67	0,06
Плиты гипсовые		1,04	0,23

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Брюханов, О.Н. Тепломассообмен: учебное пособие / О.Н. Брюханов, С.Н. Шевченко. – М.: Изд. АСВ, 2005.

2. Юдаев, Б.Н. Техническая термодинамика. Теплопередача / Б.Н. Юдаев. – М.: Высшая школа. – 1988.

3. Исаченко, В.П. Теплопередача: учебник / В.П. Исаченко, В.А.Осипова, А.С. Сукомел.– 4-е изд. – М.: Энергия. – 1981.

4. Крейт, Ф. Основы теплопередачи / Ф. Крейт, У. Блэк. – М.: Мир. – 1983.

5. Краснощеков, В.А. Задачник по теплопередаче / В.А. Краснощеков, А.С. Сукомел. – 4-е изд.– М.: Энергия. – 1980.