Дифференциальная рента за лучшую землю(R1) выше, чем за среднюю (R2), а

RL( рента за 1год)

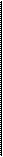SL

0 Q*L Q ( площадь в га)

Рис.2. График предложения земли.

Фиксированное предложение земли означает, что цена на землю(земельная рента, получаемая собственником земли за эксплуатацию данного ресурса в течение одного года) определяется спросом(DL) на нее. Поскольку земля используется как в сельскохозяйственной, так и в несельскохозяйственной сфере, то существует два вида спроса на землю: DLсх – сельскохозяйственный спрос; DLнсх – несельскохозяйственный спрос. Совокупный спрос на землю –DL.

DL = DLсх + DLнсх .

Следует особо отметить, что в каждый данный момент времени лучших и средних по плодородию и местоположению сельскохозяйственных земель недостаточно для удовлетворения спроса на продовольствие и продукты питания. Поэтому возникает необходимость привлекать относительно худшие по плодородию и местоположению земли. Следовательно, в каждый данный момент времени для удовлетворения спроса на продовольствие необходимо включать в эксплуатацию лучшие, средние и худшие участки земли. Указанная дифференциация земель лежит в основе существования дифференциальной земельной ренты.

Эксплуатация лучших и средних земель обеспечивает более высокую продуктивность и меньшие издержки, приходящиеся на каждую единицу произведенного продовольствия. В результате реализации продукции произведенной на указанных участках с меньшими издержками образуется некий добавочный доход, называемый дифференциальным(разностным)доходом. Этот доход при передаче его собственнику земли принимает форму дифференциальной земельной рентой. Невоспроизводимость(редкость) лучших земель и их немобильность объективно формируют особый тип монополии – монополию на землю как объект хозяйства. Этой монополией обладают те, кто ведет хозяйство на лучших и средних землях. Указанная монополия – причина дифференциального дохода, который получает землепользователь данных земель. Этот доход превращается в дифференциальную ренту при условии его передачи землевладельцу.

R

SL

R1A

MRP1=DL1

R2B

MRP2 = DL2

C

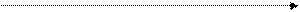0 QL(га)

MRP3 = DL3

Рис.4. Равновесие на рынке земли.

Дифференциальная рента за лучшую землю(R1) выше, чем за среднюю (R2), а

за среднюю – выше чем за худшую(0). Следовательно, дифференциальную ренту получают только владельцы лучших и средних земель. Владельцы худших земель получают абсолютную ренту, которая представляет собой ту часть дохода предпринимателя- землепользователя, которую он передает в виде арендной платы собственнику любой земли.

37. В предыдущем параграфе мы, по сути, отождествляли понятия земельная рента и цена земли. Хотя между указанными понятиями существует тесная взаимосвязь, следует выявить существенные различия между указанными понятиями.

Земельная рента – представляет собой цену услуг земли за один год.

Цена земли – представляет собой дисконтированную стоимость всей суммы рентных платежей, т.е. является капитализированной земельной рентой. Чем выше земельная рента с данного участка земли, тем выше его цена.

Представим, что некоторый участок земли приносит ежегодно земельную ренту в сумме Rn. Какую цену следует назначить покупателю за данный участок ? Мы должны определить альтернативную стоимость денежной суммы, которую следует получить от продажи земельного участка. Как мы уже знаем, в качестве альтернативы помещения денежных сумм инвесторы обычно рассматривают банковский сектор. В этом случае, цена земли должна быть равна сумме денег, положив которую в банк бывший собственник участка земли получал бы ежегодно процент на вложенный капитал равный прежде получаемой им ежегодно земельной ренте. Если текущая рыночная ставка банковского процента – r, тогда цена земли PL равна:

Rn 1

PL = ------ n , где ------ n - коэффициент дисконтирования.

(1+r) (1+r)

Поскольку покупка земли ( уплата цены земли) – бессрочное вложение капитала, то суммирование при дисконтировании начинается с единицы и продолжается до бесконечности. Более того, так как значение коэффициента дисконтирования с возрастанием «n» становится все меньше и меньше, новое количество денег, добавляемое к полученной сумме приближается к нулю, по мере того, как n приближается к бесконечности. В итоге, сумма (цена земли- PL ) в формуле достигает своего предела, когда значение ежегодной ренты – Rn за каждый цикл одинакова. Этот предел равен:

R

PL = ----- ,

r

где R – годовая земельная рента;