Достаточные признаки сходимости рядов с положительными членами: признак сравнения, Даламбера, Коши, интегральный
Признак Маклорена – Коши
Ряды, члены которых не изменяют знаки в зависимости от 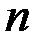 (номера), называют знакопостоянными. Ряд
(номера), называют знакопостоянными. Ряд 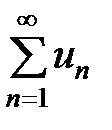 называется знакоположительным, если все члены данного ряда
называется знакоположительным, если все члены данного ряда 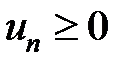 .
.
Признак сравнения
Рассмотрим ряды, члены которых не изменяют знаки в зависимости от его номера 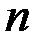 . Допустим, что члены ряда
. Допустим, что члены ряда 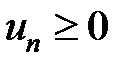 .
.
Теорема. Пусть имеем два знакоположительных ряда:
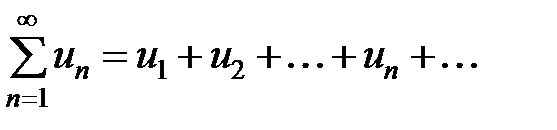 (13.12)
(13.12)
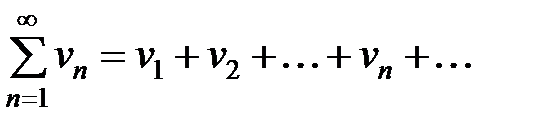 (13.13)
(13.13)
Если для всех членов этих рядов выполняются неравенства:
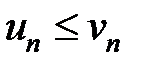 , (13.14)
, (13.14)
то из сходимости ряда с общим членом 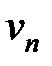 вытекает сходимость ряда
вытекает сходимость ряда 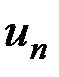 , а из расходимости ряда с общим членом
, а из расходимости ряда с общим членом 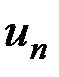 вытекает расходимость ряда с общим членом
вытекает расходимость ряда с общим членом 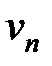 . Считаем, что неравенство (13.14) выполняется с
. Считаем, что неравенство (13.14) выполняется с 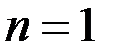 , иначе конечное число членов ряда можно отбросить.
, иначе конечное число членов ряда можно отбросить.
Отметим, что применяя признак сравнения, можно использовать ряд бесконечной убывающей геометрической прогрессии (13.8) как пример сходящегося ряда и гармонический ряд (13.10) как пример расходящегося ряда.
При решении задач чаще используется признак сравнения рядов в предельной форме, а именно: если существует конечный и отличающийся от нуля предел:
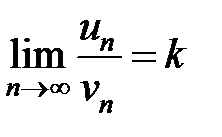
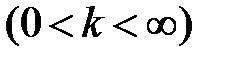 , (13.15)
, (13.15)
то оба ряда сходятся или расходятся одновременно.
Действительно, если начиная с некоторого номера выполняется условие (13.15), то для любого 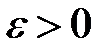
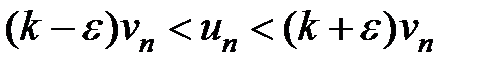 и к ряду с общим членом
и к ряду с общим членом 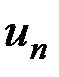 можно применить признак сравнения.
можно применить признак сравнения.
Пример 7. Исследовать на сходимость ряд 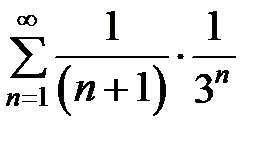 .
.
Решение.
Запишем очевидное неравенство: 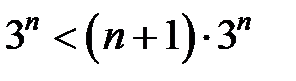 , которое имеет место при
, которое имеет место при 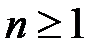 .
.
Перейдем к обратному неравенству: 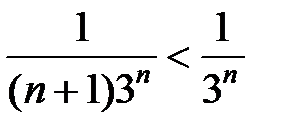 .
.
Рассмотрим два ряда: 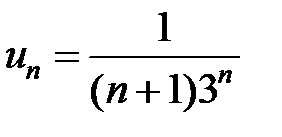 и
и 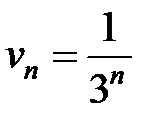 .
.
Ряд с общим членом 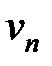 сходится как бесконечная геометрическая прогрессия со знаменателем меньше единицы.
сходится как бесконечная геометрическая прогрессия со знаменателем меньше единицы.
Следовательно, по признаку сравнения сходится и ряд с общим членом 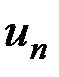 .
.
Пример 13.8. Исследовать на сходимость ряд 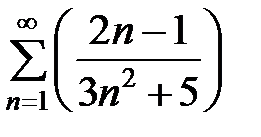 .
.
Решение.
Для сравнения возьмем ряд с общим членом 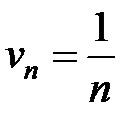 .
.
Тогда 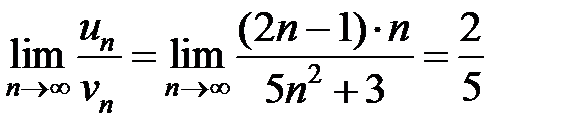 , следовательно ряды ведут себя одинаково, а именно данный ряд расходится, потому что ряд
, следовательно ряды ведут себя одинаково, а именно данный ряд расходится, потому что ряд 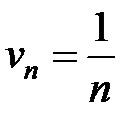 расходится как гармонический.
расходится как гармонический.
Признак Даламбера
Теорема. Пусть для ряда с знакоположительными членами 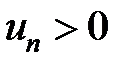 существует предел:
существует предел:
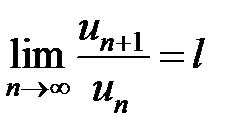 , (13.16)
, (13.16)
тогда:
1) если 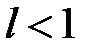 , ряд сходится;
, ряд сходится;
2) если 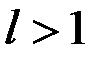 , ряд расходится;
, ряд расходится;
3) если 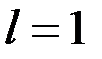 , признак не дает ответ.
, признак не дает ответ.
Пример 9. Исследовать на сходимость ряд 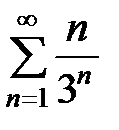 .
.
Решение.
Обозначим 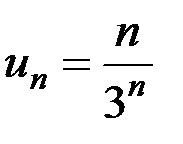 , тогда
, тогда 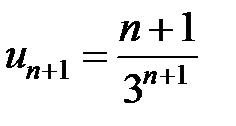 .
.
Найдем отношение следующего члена ряда к предыдущему:
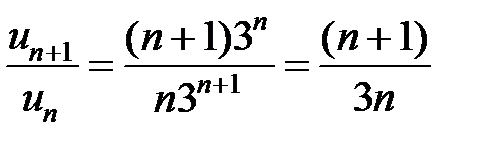
и возьмем его предел.
Получим: 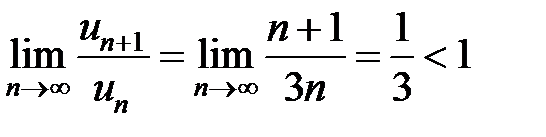 .
.
Таким образом, по признаку Даламбера ряд сходится.
Пример 10. Исследовать на сходимость ряд 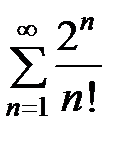 .
.
Решение.
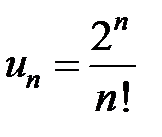 ,
, 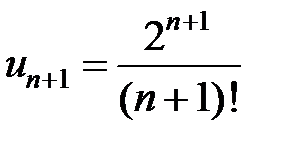 .
.
Запишем отношение 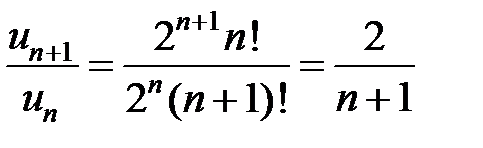 и найдем его предел:
и найдем его предел:
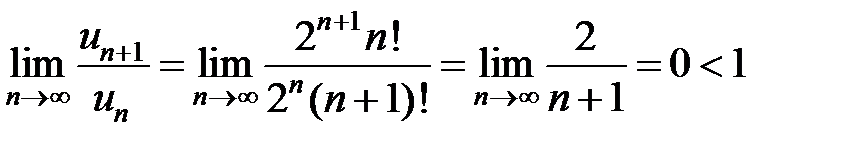 .
.
Таким образом, по признаку Даламбера ряд сходится.
Пример 11. Исследовать на сходимость ряд 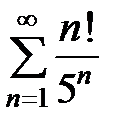 .
.
Решение.
Обозначим 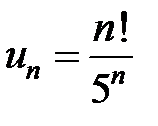 , тогда
, тогда 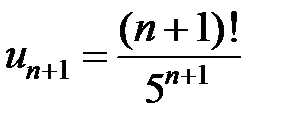 .
.
Найдем отношение 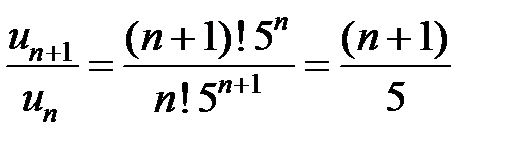 и возьмем его предел:
и возьмем его предел:
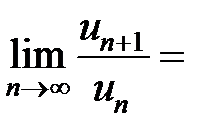
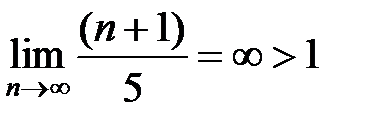 ,
,
то есть по признаку Даламбера ряд расходится.
