БИЛЕТ 6. Теоремы сравнения. Признак Даламбера. Признак Коши

БИЛЕТ 1. Преобразование Лапласа. Оригиналы и их изображения. Свойства преобразования Лапласа: линейность, подобие, смещение, запаздывание.

Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию 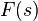комплексного переменного (изображение) с функцией 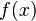вещественного переменного (оригинал).

Функция f(t) называется оригиналом, если выполняются 3 свойства:

1) функция тождественна 0 при t<0

2) f(t) кусочно непрерывна при t≥0

3) |f(t)|≤M*e^σt, где М и σ- числа

Поэтому основные элементарные функции можно считать оригиналами, если считать, что при t<0 они обращаются в 0.

Изображением оригинала f(t) по Лапласу называется функция F(p)=инт от 0 до +беск f(t)*e^-ptdt, где з-любое комплексное число

1. Свойство линейности: L(f1(t)+f2(t))=F1(p)+F2(p)

L*C*f(t)=C*F(p), где L-оператор Лапласа

2. Свойство подобия: f(αt)ß1\α*F(p\α)

3. Теорема смещения: e^αt*f(t)ßF(p-α)

4. Свойство запаздывания: f(t-α)ße^-pαF(p)

БИЛЕТ 2. Свойства преобразования Лапласа: дифференцирование оригинала, дифференцирование изображения, интегрирование оригинала, интегрирование изображения.

Дифференцирование оригинала: f(t)ßp*F(p)-f(0)

f’’(t)ßp²*F(p)-p*f(0)-f’(0)

f’’’(t)ßp³F(p)-p²*f(0)-βf’(o)-f’(0)

Дифф-е изображения:

t*f(t)ß-1F’(p)

tⁿf(t)ß(-1)ⁿFⁿ(p)

Интегрирование оригинала:

F(p)\pàинт. от 0 до t f(t)dt

Интегрирование изображения:

f(t)\tßинт. от 0 до +беск F(p)dp

БИЛЕТ 3. Операционный метод решения линейных дифференциальных уравнений и их систем.

y’’+a1y’+a2y=f(x). Уравнение принимает вид:

x’’(t)+a1x’(t)+a2x(t)=f(t). Изображаем по Лапласу обе части уравнения, для этого обозначим:

x(t)ßX(p)

x’(t)ßpX(p)-x(0)

x’’(t)ßp2X(p)-px(0)-x’(0)

f(t)ßF(p). Подставляем, преобразовываем. По полученному изображению X(p) восстанавливаем оригинал x(t).

Для решения систем:

1) с помощью таблицы преобразования Лапласа перейдем от оригиналов к соответствующим изображениям.

2) Подставим найденные изображения в исходное уравнение

3) Теперь в левых частях уравнений нужно собрать все слагаемые, в которых присутствует X(p) или Y(p) В правые части уравнений собрать все остальные слагаемые.

4) Далее в левой части каждого уравнения проводим вынесение за скобки. Полученную систему решают по формулам Крамера. Вычисляют главный определитель системы.

5) По формулам Крамера вычисляют еще два определителя, для x и для y. Корни находят, разделив найденные определители на главный. В итоге получают операторное решение системы.

6) Используя таблицу, перейдем от изображений к соответствующим оригиналам

7) Подставим полученные изображения в операторное решение системы.

БИЛЕТ 4. Числовые ряды. Сходимость и сумма ряда. Свойства сходящихся рядов.

Пусть а1, а2…аn числовая последовательность. Сумма a1+a2+…+an называется числовым рядом, и обозначается ∑an=a1+a2+…+an

Сумму первых n членов ряда называется частичной суммой и обозначается Sn

Если последовательность частичных сумм Sn имеет конечный предел S, при nàбеск., то ряд назыввют сходящимся и его сумма равна S.

Ели предел частичной суммы не существует или бесконечен, то ряд называю расходящимся.

Свойства сходящихся рядов:

1. Если ряд сходится, то последовательность его членов стремится к нулю.

2. Сумма двух сходящихся рядов есть сходящийся ряд, причём его сумма равна сумме первого + сумма второго. Таким образом, сходящиеся ряды можно почленно складывать, а с учётом теоремы 1 и вычитать.

1. Если ряд сходится, то сходится и любой его остаток, и, наоборот, если сходится какой-либо остаток ряда, то и сам ряд также сходится.

БИЛЕТ 5. Необходимый признак сходимости. Пример. Гармонический ряд.

Необходимый признак: Если ряд ∑an сходится, то его общий член anà0. Обратное неверно.

Примером такого рода является гармонический ряд ∑1/n. an=1/nà0, но ряд-расходящийся.

Следствие: если общий член ряда не стремится к 0, то ряд расходится.

БИЛЕТ 6. Теоремы сравнения. Признак Даламбера. Признак Коши.

1. Признак сравнения. Пусть ряды ∑an и ∑bn знакоположительные и для всех n из множества натуральных чисел выполняется неравенство an≤bn. Тогда если ряд ∑an расходится, то и второй тоже. Если ∑bn сходится то и второй сходится.

2. Предельный признак сравнения: Пусть ряды ∑an и ∑bn знакоположительные. Если число С=lim an/bn принадл. (0,+беск), то ряды сходятся или расходятся одновременно.

3. Признак Коши: Пусть ряд ∑an знакоположительный. Если число К=lim корень n-ой степени от an<1,,, то ряд сходится

Если К>1, то ряд расходится

Если К=1, то о сходимости-расходимости ничего сказать нельзя.

4. Признак Даламбера: Пусть ∑an знакоположительный, если число D=lim an+1/an<1, ряд сходится

D>1. расходится

D=1, то ничего нельзя сказать