Разложение многочлена на множители. Теория.

Тест 6

Вопрос 1Выражение 3х²+2х+1-х³, называется
а.) многочленом второй степени	б.) полиномом второй степени	в.) целой рациональной функцией от х	г.) полиномом третьей степени
Вопрос 2Какие значения являются корнем многочлена х³+3х²+4х-8
а.) 1	б.) 0	в.) -2+2i	г.) -2-2i
Вопрос 3Чему равен остаток при делении многочлена f(x)=х⁴+2х³+3х²+4х+5 на разность х-1
а.) 5	б.) 15	в.) 1	г.) -1
Вопрос 4Чему равен остаток при делении многочлена f(x)=х⁴+2х³+3х²+4х+5 на разность х+1
а.) 3	б.) 5	в.) 1	г.) -1
Вопрос 5Чему равен остаток при делении многочлена f(x)=х⁴+2х³-3х²+4х-4 на разность х-1
а.) 1	б.) -1	в.) 0	г.) 2
Вопрос 6Какие из выражений являются алгебраическими уравнениями
а.) х³+3х²+4х-8	б.) х³+3х²+4х-8=0	в.)	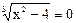г.)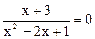
Вопрос 7Всякое, ли уравнение имеет корни?
а.) да, но только действительные	б.) да, но только комплексные	в.) да, и корни могут быть действительными, или комплексными	г.) нет
Вопрос 8Всякое, ли алгебраическое уравнение имеет корни?
а.) да, но только действительные	б.) да, но только комплексные	в.) да, и корни могут быть действительными, или комплексными	г.) нет
Вопрос 9Сколько всего корней имеет многочлен f(x)=х⁴+2х³-3х²+4х-4
а.) один	б.) два	в.) три	г.) четыре
Вопрос 10Сколько всего корней имеет многочлен f(x)=х⁴+3х³+х²-3х-2
а.) один	б.) два	в.) три	г.) четыре
Вопрос 11В многочлене f(x)=х⁴+2х³-3х²-4х+4 корень х=1 является
а.) однократным	б.) двукратным	в.) трёхкратным	г.) четырёхкратным
Вопрос 12В многочлене f(x)=х⁴+3х³+х²-3х-2
а.) х=-1 двукратный, х=1 и х=-2 − однократные	б.) х=-1 и х=-2 − двукратные	в.) х=1 и х=-2 − двукратные	г.) х=-1 двукратный, х=1 и х=2 − однократные
Вопрос 13Сколько всего корней имеет многочлен f(x)=х⁴+1
а.) корней нет	б.) два действительных и два сопряжённых комплексных	в.) две пары сопряжённых комплексных корней	г.) два двукратных сопряжённых комплексных корня
Вопрос 14Какую степень имеет многочлен f(x)=х(х-2)²(х+2)(х-1)³
а.) 3	б.) 4	в.) 6	г.) 7
Вопрос 15Какую степень имеет многочлен f(x)=х(х²+1)²(х-1)³
а.) 8	б.) 7	в.) 5	г.) 3
Вопрос 16Если многочлен имеет двукратный корень 3-2i, то
а.) -3+2i двукратный корень	б.) 3+2i однократный корень	в.) 3+2i двукратный корень	г.) других комплексных корней нет
Вопрос 17Произведение двух множителей, соответствующих сопряжённым комплексным корням, можно представить в виде
а.) квадратного трёхчлена с комплексными коэффициентами	б.) квадратного трёхчлена с вещественными коэффициентами	в.) полинома второй степени с действительными коэффициентами	г.) полинома четвёртой степени с действительными коэффициентами
Вопрос 18Полярные координаты точки М(r; j)
а.) r - полярный радиус, j - полярный угол;	б.) j - полярный радиус, r - полярный угол;	в.) r - абсцисса, j - ордината;	г.) r - ордината, j - абсцисса;
Вопрос 19Пусть М(х; у)«М(r; j), тогда
а.) х=r·cosj	б.) y=r·sinj	в.) y=r·cosj	г.) x=r·sinj
Вопрос 20Пусть М(х; у)«М(r; j), тогда
а.)	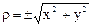б.)	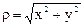в.)	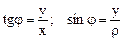г.)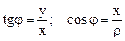
Вопрос 21Какую наименьшую степень может иметь многочлен, в котором: х=-2 – однократный; х=3 – двукратный; больше действительных корней нет; х=2-3i – однократный:
а.) 4	б.) 5	в.) 6	г.) 7
Вопрос 22Какую степень может иметь многочлен, в котором: х=-2 – однократный; х=3 – двукратный; больше действительных корней нет; х=2-3i – однократный:
а.) 4	б.) 5	в.) 6	г.) 7