Предел последовательности.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ
(образован в 1953 году)

Кафедра физики и высшей математики
| Дистанционное обучение | Физ. мат 4.15.2701 очн. плн. Физ. мат 4.15.2701 очн. скр. Физ. мат 4.15.2701 зчн. плн. Физ. мат 4.15.2701 зчн. скр. Физ. мат 4.15.2703 очн. плн. Физ. мат 4.15.2703 очн. скр. Физ. мат 4.15.2703 зчн. плн. Физ. мат 4.15.2703 зчн. скр. Физ. мат 4.15.2704 очн. плн. Физ. мат 4.15.2704 очн. скр. Физ. мат 4.15.2704 зчн. плн. Физ. мат 4.15.2704 зчн. скр. Физ. мат 4.15.2705 очн. плн. Физ. мат 4.15.2705 очн. скр. Физ. мат 4.15.2705 зчн. плн. Физ. мат 4.15.2705 зчн. скр. Физ. мат 4.15.2707 очн. плн. Физ. мат 4.15.2707 очн. скр. | Физ. мат 4.15.2707 зчн. плн. Физ. мат 4.15.2707 зчн. скр. Физ. мат 4.15.2708 очн. плн. Физ. мат 4.15.2708 очн. скр. Физ. мат 4.15.2708 зчн. плн. Физ. мат 4.15.2708 зчн. скр. Физ. мат 4.15.2710 очн. плн. Физ. мат 4.15.2710 очн. скр. Физ. мат 4.15.2710 зчн. плн. Физ. мат 4.15.2710 зчн. скр. Физ. мат 4.15.2712 очн. плн. Физ. мат 4.15.2712 очн. скр. Физ. мат 4.15.2712 зчн. плн. Физ. мат 4.15.2712 зчн. скр. Физ. мат 4.15.2713 очн. плн. Физ. мат 4.15.2713 очн. скр. Физ. мат 4.15.2713 зчн. плн. Физ. мат 4.15.2713 зчн. скр. |
М.С. Алборова
«Высшая математика»
Часть II.
Учебно-методические указания по проведению практических занятий для студентов
Дневной и заочной форм обучения.

Www.msta.ru
Москва – 2006
УДК 51
© Алборова М.С.. Высшая математика. Учебное пособие для студентов технологических и механических специальностей, всех форм обучения. - МГУТУ, 2006 г.
Настоявшее пособие составлено с целью оказания помощи студентом в приобретении навыков по решению задач курса:математический анализ.
В начале каждого раздела помещены определения, теоремы, формулы и другие краткие сведения по теории; затем приводятся подробные решения типичных примеров; в конце каждого раздела содержатся примеры для самостоятельного решения. В конце пособия приведены контрольные задания являющиеся типовыми расчетами по данным разделам.
Автор: доц. к.ф.-м.н. Алборова М.С.
Рецензенты: доц. Гофман В.Г.
Редактор: Свешникова Н.И.
© Московский государственный университет технологий и управления, 2006 г.
109004, Москва, Земляной вал, 73
| Содержание | |
| Занятие 1. | |
| 1.Функция. Область определения. | |
| Контрольные вопросы. Задания. | |
| Занятие 2. | |
| 1.Предел последовательности. | |
| 2.Предел функции. | |
| 3.Вычисление пределов функции с помощью замены бесконечно малых на эквивалентные. | |
| Контрольные вопросы. Задания. | |
| Занятие 3. | |
| 1. Непрерывность функции. | |
| Контрольные вопросы. Задания. | |
| Занятие 4. | |
| 1. Производная функция | |
| 2. Понятие дифференциала. | |
| 3. Производные высших порядков. | |
| Контрольные вопросы. Задания. | |
| Занятие 5. | |
| 1.Теоремы Ролля, Лагранжа, Коши. Формула Тейлора. | |
| Контрольные вопросы. Задания. | |
| Занятие 6. | |
| 1. Правило Лопиталя. | |
| Контрольные вопросы Задания. | |
| Занятие 7. | |
| 1.Касательная и нормаль к кривой. | |
| Контрольные вопросы. Задания. | |
| Занятие 8. | |
| 1.Неопределенный интеграл. | |
| 2.Замена переменной в неопределённом интеграле. | |
| 3.Интегрирование по частям. | |
| Контрольные вопросы. Задания. | |
| Занятие 9. | |
| 1.Определённый интеграл | |
| 2. Вычисление площадей плоских фигур. | |
| 3. Вычисление объёмов тел вращения. | |
| 4.Формулы длин дуг плоских кривых. | |
| Контрольные вопросы. Задания. | |
| Занятие 10. | |
| 1.Несобственные интегралы. | |
| Контрольные вопросы. Задания. | |
| Типовой расчет по теме «Предел и производная» |
Математический анализ.
Занятие 1.
1.Функция. Область определения.
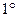 Понятие функции. Пусть Х и У – два множества вещественных чисел. Если каждому элементу х из множества Х по некоторому правилу ставится в соответствие единственное число
Понятие функции. Пусть Х и У – два множества вещественных чисел. Если каждому элементу х из множества Х по некоторому правилу ставится в соответствие единственное число 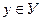 , то говорят, что на множестве Х задана функция, область значения которой расположена в У. Это можно записать так:
, то говорят, что на множестве Х задана функция, область значения которой расположена в У. Это можно записать так:
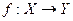 .
.
Множество Х- называют областью определения функции, а множество У, состоящее из всех чисел вида 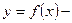 множеством значений функции.
множеством значений функции.
Если у является функцией от х, то пишут 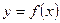 . Область определения обозначается через
. Область определения обозначается через 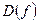 , а множество значений – через
, а множество значений – через 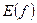 .
.
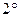 Основные элементарные функции. Основными элементарными функциями называют следующие функции:
Основные элементарные функции. Основными элементарными функциями называют следующие функции:
1) степенная функция 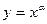 ,
, 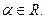
2) показательная функция 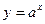 , где а- любое положительное число, отличное от единицы:
, где а- любое положительное число, отличное от единицы: 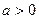 ,
, 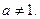
3) логарифмическая функция 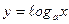 , где а- любое положительное число, отличное от единицы:
, где а- любое положительное число, отличное от единицы: 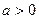 ,
, 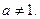
4) тригонометрические функции: 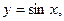
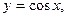
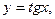
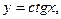
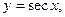
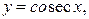
5) обратные тригонометрические функции: 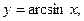
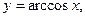
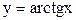
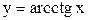 ,
, 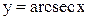 ,
, 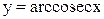 .
.
Элементарными называются функции, получающиеся из основных элементарных функций с помощью четырёх арифметических действий и применённых конечное число раз.
Пример неэлементарной функции:
|
|
|
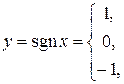
Графиком функции 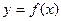 называется множество точек плоскости хОу с координатами
называется множество точек плоскости хОу с координатами 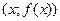 , где
, где 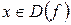 .
.
Функция 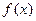 , область определения которой симметрична относительно нуля, называется чётной, если
, область определения которой симметрична относительно нуля, называется чётной, если 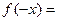
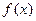 для
для 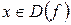 и нечётной, если
и нечётной, если 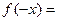
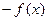 ,
, 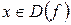 .
.
Произведение двух нечетных функций является четной функцией.
Функция 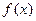 называется периодической, если существует положительное число Т такое, что при
называется периодической, если существует положительное число Т такое, что при 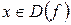 и
и 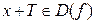 выполняется равенство
выполняется равенство 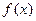 =
= 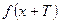 .
.
Пример 1. Найти область определения функции 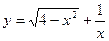 .
.
Решение. Данная функция определена, если 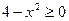 и
и 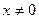 . Решаем эту систему:
. Решаем эту систему:
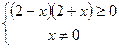
 |
Ясно, что искомое неравенство имеет место при 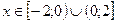 , значит полученное множество есть область определения данной функции.
, значит полученное множество есть область определения данной функции.
Пример 2. Установить чётность или нечётность функции 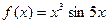 .
.
Решение. Для данной функции область определения симметрична относительно нуля: 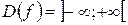 .
.
Заменяя х на –х, получим 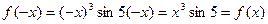 , т.е.
, т.е. 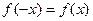 . Итак, данная функция чётная.
. Итак, данная функция чётная.
Пример 3. Найти основной период функции 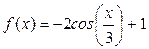 .
.
Решение. Так как основной период функции 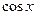 есть
есть 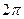 , то основной период функции
, то основной период функции 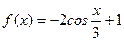 есть
есть 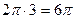 , т.е.
, т.е. 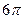 .
.
Контрольные вопросы.
1.Элементарные функции и их графики.
2.Понятие функции. Область определения.
Задания.
1) Найти область определения функции:
а) 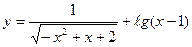 б)
б) 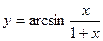
в) 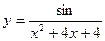 г)
г) 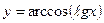 .
.
2) Какая из функций является чётной, какая нечётной:
а) 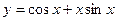 б)
б) 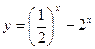
г) 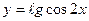 д)
д) 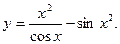
3) Найти периоды функций:
а) 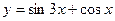 , б)
, б) 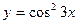 .
.
Занятие 2.
Предел последовательности.
10 Функцию 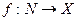 натурального аргумента называют последовательностью. Если Х=R, т.e. f(n)-вещественные числа, где
натурального аргумента называют последовательностью. Если Х=R, т.e. f(n)-вещественные числа, где 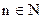 , то такую последовательность назовём числовой и обозначим
, то такую последовательность назовём числовой и обозначим 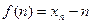 -ый член последовательности, а саму последовательность
-ый член последовательности, а саму последовательность
|
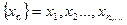
20.Число 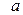 называется пределом последовательности
называется пределом последовательности 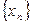 , если для любого числа
, если для любого числа 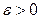 , найдется такое натуральное число
, найдется такое натуральное число 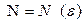 , что при всех
, что при всех 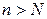 выполняется неравенство:
выполняется неравенство:
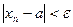
При этом пишут 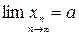 , или
, или 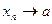 при
при 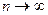 и число а называют пределом последовательности
и число а называют пределом последовательности 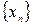 . Говорят также , что последовательность
. Говорят также , что последовательность 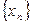 сходится к
сходится к 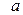 .
.
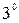 Справедливы следующие утверждения:
Справедливы следующие утверждения:
|
|
|
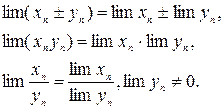
| |
| |
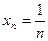 . Доказать, что
. Доказать, что 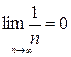
Решение. В самом деле, зададим произвольное 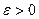 и решим неравенство
и решим неравенство 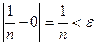 или
или 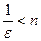 .Следовательно, для всякого
.Следовательно, для всякого 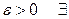
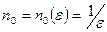 такое, что неравенство
такое, что неравенство 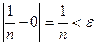 - выполняется для всех n>n0,, ч.т.д.
- выполняется для всех n>n0,, ч.т.д.
Пример 2. Если 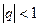 , то
, то 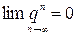 .
.
Доказательство. Пусть пока 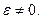 Неравенство
Неравенство 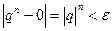 верно, если
верно, если 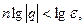 т.е. если
т.е. если 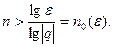 Таким образом, мы доказали, что
Таким образом, мы доказали, что 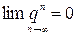 при
при 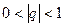 .
.
Пример 3. Пусть 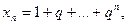
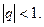
Доказать, что 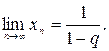
Доказательство. Имеем 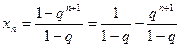 . Так как
. Так как 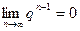 при
при 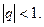 (см. пример 2), то, применяя формулы (2) и (3), получим:
(см. пример 2), то, применяя формулы (2) и (3), получим:
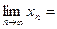
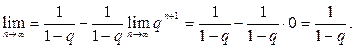
Пример 4. Показать, что при 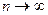 последовательность
последовательность 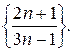 Имеет пределом
Имеет пределом 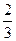 .
.
Решение. Здесь 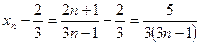 . Определим при каком
. Определим при каком 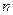 выполняется неравенство
выполняется неравенство 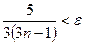 . Так как
. Так как 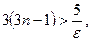 то
то 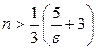 .
.
Итак, если 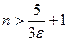 , то
, то 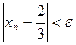 , т.е.
, т.е. 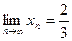 .
.
Предел функции.
Пусть 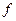 определена в окрестности точки
определена в окрестности точки 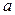 , за исключением, быть может точки
, за исключением, быть может точки 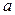
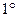 Определение по Коши. Число А называется пределом функции
Определение по Коши. Число А называется пределом функции 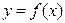 при
при 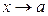 ( в точке
( в точке 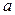 ), если для каждого числа
), если для каждого числа 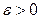 можно найти такое число
можно найти такое число 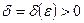 , что
, что 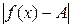 будет меньше
будет меньше 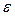 , когда
, когда 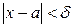 , при
, при 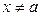 .
.
При этом пишут 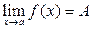 или
или 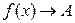 при
при 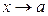 .
.
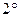 Определение по Гейне. Число А называется пределом функции
Определение по Гейне. Число А называется пределом функции 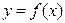 в точке
в точке 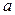 , если для любой последовательности
, если для любой последовательности 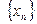 , где,
, где, 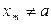 ,
, 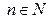 , сходящейся к
, сходящейся к 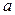 , (т.е.
, (т.е. 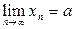 ), последовательность соответствующих значений функций
), последовательность соответствующих значений функций 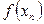 ,
, 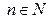 , сходится к числу А, (т.е.
, сходится к числу А, (т.е. 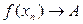 ).
).
Эти два определения равносильны.
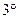 Функцию
Функцию 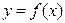 называют бесконечно большой при
называют бесконечно большой при 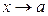 , если для всякого числа М>0 существует зависящее от М число
, если для всякого числа М>0 существует зависящее от М число 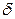 , такое, что
, такое, что 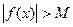 при всех
при всех 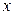 удовлетворяющих неравенству
удовлетворяющих неравенству 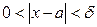 . Записывают коротко
. Записывают коротко 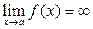 или
или 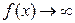 при
при 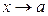 .
.
 Функцию
Функцию 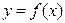 называют бесконечно малой при
называют бесконечно малой при 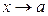 , если
, если 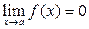
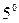 Справедливые свойства:
Справедливые свойства:
1) 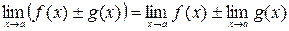 ;
;
2) 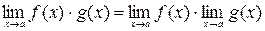 ;
;
3) 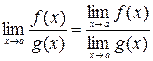 , (при
, (при 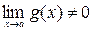 ).
).
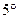 Первый замечательный предел:
Первый замечательный предел: 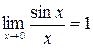 .
.
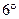 Второй замечательный предел:
Второй замечательный предел: 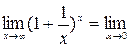
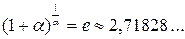
Пример 1. Найти следующие пределы:
а) 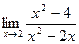 ; б)
; б) 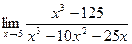 .
.
Решение. а) 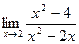 , здесь числитель и знаменатель дроби при
, здесь числитель и знаменатель дроби при 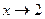 стремится к нулю (неопределённость вида
стремится к нулю (неопределённость вида 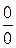 ).
).
Имеем 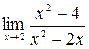 =
= 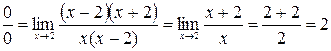 .
.
Итак, 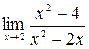 =2.
=2.
б) 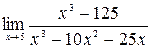 =
= 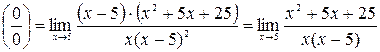 ;
;
числитель дроби стремится к 75, а знаменатель стремится к нулю, т.е. является бесконечно малой величиной, следовательно, рассматриваемая дробь – бесконечно большая величина и 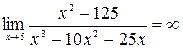 .
.
Пример 2. Вычислить 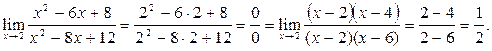
Итак, 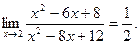
Пример 3. Найти пределы:
а) 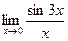 , б)
, б) 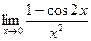 .
.
Решение. а) 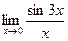 =
= 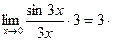
б) 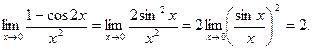 .
.
Пример 4. Найти пределы:
а) 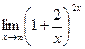 б)
б) 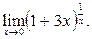
Решение. а) 
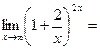
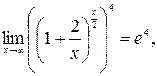
б)