Тема 1.3.2- 1.3.3 Размещения, перестановки, сочетания

Правила суммы и произведения – это общие правила решения комбинаторных задач. Кроме них в комбинаторике пользуются формулами для подсчета числа отдельных видов комбинаций, которые встречаются наиболее часто. Рассмотрим некоторые из них.

Используя цифры 7,4 и 5образовать всевозможные двузначные числа.

Решение: 77, 74, 75, 47, 44, 57, 54, 55.

Мы образовали различные кортежи длины 2 с повторяющимися элементами из трех цифр. В комбинаторике такие кортежи называют размещениями с повторениями из трех элементов по два элемента.

Определение. Размещение с повторениями из k элементов по m элементов – это кортеж длины m, составленный из m элементов k элементного множества.

Таким образом два размещения из k элементов по m элементов отличаются друг от друга либо составом элементов, либо порядком их расположения.

Возникает вопрос: «Сколько всевозможных размещений по m элементов каждое можно образовать из k элементов данного множества?».

Обозначают число всевозможных размещений с повторениями из k элементов по m элементов – А .

Выведем эту формулу.

Пусть в множестве Хсодержится k элементов. Будем образовывать из них различные кортежи по m элементов. Такие кортежи образуют множество Х х Х х … Х, содержащее m множителей. По правилу произведения

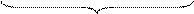
n(Х х Х х …х Х) = n(Х) х n(Х)… n (Х) = k х k … х k = k^m

m множителей m множителей

Таким образом А _лⁿ = k^m

Пользуясь формулой, легко посчитать (смотри задачу выше), что

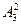= 3² = 9, т.к. речь идет о размещениях с повторениями из трех элементов по два.

Задача: Из цифр 7,4 и 5 составить двузначные числа, чтобы цифры в записи числа не повторялись.

Решение: 74, 75, 47, 45, 57, 54.

Таким образом, встречаются задачи, в которых требуется подсчитать числа кортежей длины m, образованных из k элементов некоторого множества, при условии что, элементы в кортеже не повторяются. Такие кортежи называются размещениямибез повторений из k элементов по m элементов.

Определение. Размещение без повторений из k элементов по m элементов – это кортеж длины m, составленный из неповторяющихся элементов множества, в котором k элементов.

Обозначается 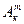- читается: число размещений без повторений из k элементов по m элементов.

Выведем эту формулу:

Пусть k = n (x). Будем образовывать из них различные размещения без повторений из m элементов. Тогда выбор первого элемента можно осуществить k способами, выбор второго (k – 1) способом (т.к. после выбора первого элемента кортежа в множестве Хостается k -1 элемент). Третий элемент можно выбрать k -2 способами и т.д., третий элемент можно выбрать k- (m -1) способами.

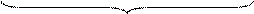Значит, 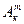= k (k – 1) (k – 2) … (k – m + 1)

m множителей

Задача: Сколько всевозможных трехзначных чисел можно записать, используя цифры 7,4,5, чтобы числа не повторялись?

Решение. В задаче рассматриваются размещения без повторений из трех элементов по три, и их число можно подсчитать по формуле:

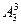= 3 (3 – 1)(3 – 2) = 6.

Числа: 745, 754, 457, 475, 547, 574.

Заметим, что в данном случае разные числа получаются в результате перестановки цифр. Поэтому размещения из k элементов по k элементов называется перестановкамииз k элементов без повторений.

Обозначают P_k и вычисляютпо формуле:

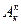= P_k

Читают: число перестановок без повторений из k элементов.

P_k = k! (k! = 1 х 2 х 3 … k, читают «k факториал» например, 5! = 1 х 2 х 3 х 4 х 5 = 120).

Из элементов множества Х = {7,4,5} можно образовать не только кортежи различной длины, но и различные подмножества. В комбинаторике их называют сочетаниями без повторений.

Определение. Сочетание без повторений из k элементов – это m – элементное подмножество множества, содержащего k элементов.

Два сочетания из k элементов по m элементов отличаются друг от друга хотя бы одним элементом.

Обозначается: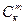

Читают: число сочетаний без повторений из k элементов по m элементов.

Образуем различные двухэлементные подмножества из элементов множества Х = 7,4,5. Их будет три: 7,4 ; 7,5 ; 4,5. Из элементов каждого такого подмножества можно образовать 2 кортежа длины 2.

(7,4) (7,5) (4,5)

(4,7) (5.7) (5,4)

Все полученные кортежи являются размещениями без повторений из трех элементов по два и их число равно 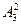= 3х2 = 6.

т.е. =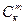

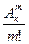
Пусть n (Х) = k. Образуем из них сочетания без повторений по m элементов. Они будут представлять собой m – элементные подмножества множества Х. Всего таких подмножеств будет 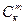. Из элементов каждого подмножества можно образовать m! перестановок, т.е. кортежей длины m

В итоге получим m ! х 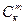кортежей длины m , образованных из k элементов множества х. Их число равно .

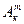
Таким образом 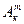= m! х 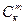à 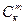=