В2.2. Перестановки, размещения, сочетания
В2.1. Принцип умножения
Комбинаторика – раздел математики, в котором изучаются методы подсчета числа комбинаций определенного вида, составленных из элементов определенного множества.
Основным в элементарной комбинаторике является принцип умножения.
Принцип умножения.
Пусть требуется выполнить одно за другим n действий, причем 1-е действие можно выполнить k1 способами; 2-е – k2 способами; 3-е – k3 способами;…; n-е - kn способами. И число способов, которыми можно выполнить каждое действие, не зависит от того, какие способы были выбраны для выполнения предшествующих действий. Тогда число способов, которыми можно выполнить все n действий, равно произведению k1 × k2 × k3 × ... × kn. Это и есть принцип умножения. Проще всего объяснить справедливость принципа умножения можно при помощи диаграммы (рис. 2).
Пример.
У человека имеется 3 рубашки (Р1, Р2, Р3), 2 галстука (Г1, Г2) и 2 пары ботинок (Б1, Б2). Он признает любое сочетание этих элементов. Сколькими способами он может одеться?
Решение.
Чтобы одеться, человек должен выполнить одно за другим и независимо одно от другого 3 действия:
1. Выбрать рубашку (три способа).
2. Выбрать галстук (два способа).
3. Выбрать ботинки (два способа).
Все способы выбора костюма показаны на диаграмме (рис. 2).
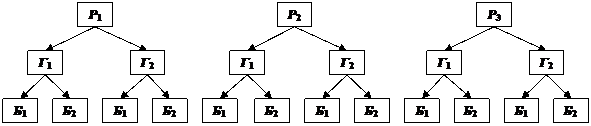

Рис. 2
Всего можно одеться 3 × 2 × 2 = 12 способами.
Некоторые свойства биномиальных коэффициентов
1. 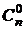 = = 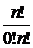 = 1. = 1. | 2. 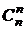 = = 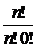 = 1. = 1. |
3. 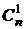 = = 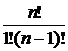 = n. = n. | 4. 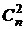 = = 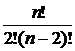 = = 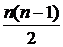 . . |
5. 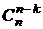 = = 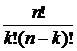 = = 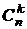 . . | |
6. 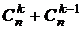 = = 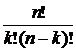 + + 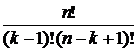 = = 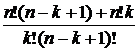 = = = = 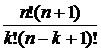 = = 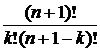 = = 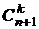 . . |
Пример 2. Сколькими способами 8 человек можно распределить по двум комнатам, если в каждой должно быть не менее трех человек?
Решение. Варианты распределения людей по комнатам таковы.
Вариант 1: в первой комнате – 3 человека; во второй – 5 человек.
Вариант 2: в первой комнате – 4 человека; во второй – 4 человека.
Вариант 3: в первой комнате – 5 человек; во второй – 3 человека.
Чтобы задать распределение, необходимо (и достаточно) назвать людей, которые остаются в первой комнате, остальные перейдут во вторую. При этом порядок перечисления не важен.
Выбрать трех человек для первой комнаты можно n1 = 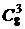 =
= 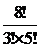 = 56 способами. Выбрать четырех человек для первой комнаты можно n2 =
= 56 способами. Выбрать четырех человек для первой комнаты можно n2 = 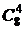 =
= 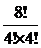 = 70 способами. Выбрать пять человек для первой комнаты можно n3 =
= 70 способами. Выбрать пять человек для первой комнаты можно n3 = 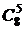 =
= 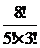 =
= 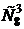 = 56 способами. Число всех способов разместить людей равно n1 + n2 + n3= 56 + 70 + 56 = 182.
= 56 способами. Число всех способов разместить людей равно n1 + n2 + n3= 56 + 70 + 56 = 182.
Пример 3.
Сколько всего существует различных последовательностей, состоящих из нулей и единиц, в каждой из которых m нулей и n единиц.
Решение. Чтобы задать такую последовательность, надо выполнить одно действие – выбрать из (n + m) позиций для цифр m позиций для нулей (n позиций для единиц). Число способов выполнить это действие равно 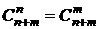 .
.
Например, если m = 2, n = 3, то 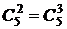 =10. Эти последовательности таковы: 01101, 00111, 10011, 11100, 10101 и т.д.
=10. Эти последовательности таковы: 01101, 00111, 10011, 11100, 10101 и т.д.
Пример 2.
Число неотрицательных решений в целых числах уравнения 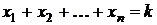 равно
равно 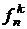 , ведь всякое решение
, ведь всякое решение 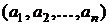 данного уравнения можно трактовать, как сочетание с повторениями, содержащее
данного уравнения можно трактовать, как сочетание с повторениями, содержащее 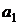 элементов первого типа (
элементов первого типа ( 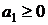 ),
), 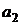 элементов второго типа (
элементов второго типа ( 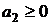 ), …,
), …, 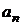 элементов n го типа (
элементов n го типа ( 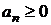 ),
), 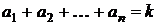 .
.
В2.4. Бином Ньютона
Утверждение. Справедлива формула (формула бинома Ньютона)
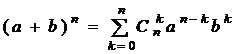 .
.
Доказательство. Воспользуемся методом математической индукции.
1).База индукции.
( 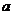 +
+ 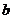 )1=
)1= 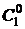
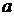 1
1 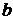 0+
0+ 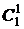
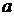 0
0 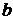 1 =
1 = 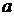 +
+ 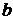 ;
;
( 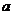 +
+ 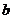 )2=
)2= 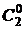
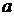 2×
2× 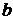 0+
0+ 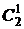
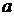
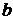 +
+ 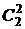
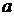 0
0 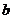 2=
2= 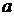 2+2
2+2 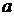
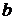 +
+ 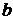 2.
2.
2).Индуктивное предположение. Положим, что

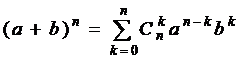 .
.
3).Индуктивный переход.
Доказав истинность следующей формулы, мы докажем истинность бинома Ньютона.
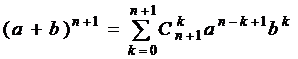 .
.
Проведем преобразования и воспользуемся индуктивным предположением.
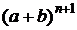 =
= 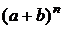 ×
× 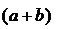 =
= 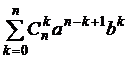 +
+ 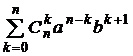 =
=
= 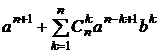 +
+ 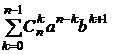 +
+ 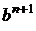 =
= 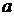 n+1 +
n+1 +
+ 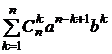 +
+ 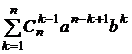 +
+ 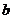 n+1.
n+1.
Во второй сумме была сделана замена переменной, чтобы индекс суммирования менялся не от 0 до n - 1, а от 1 до n.
Объединим две суммы и воспользуемся тем, что 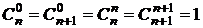 ;
; 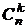 +
+ 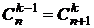 .
.
Продолжим преобразования
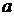 n+1
n+1 +
+ 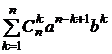
 +
+ 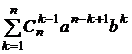 +
+ 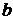 n+1=
n+1=
= 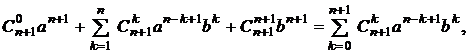

что и требовалось доказать.
Пример.
24 = 16 = 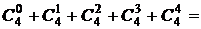 1 + 4 + 6 + 4 + 1.
1 + 4 + 6 + 4 + 1.
0 = 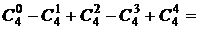 1 - 4 + 6 - 4 + 1.
1 - 4 + 6 - 4 + 1.
В2.1. Принцип умножения
Комбинаторика – раздел математики, в котором изучаются методы подсчета числа комбинаций определенного вида, составленных из элементов определенного множества.
Основным в элементарной комбинаторике является принцип умножения.
Принцип умножения.
Пусть требуется выполнить одно за другим n действий, причем 1-е действие можно выполнить k1 способами; 2-е – k2 способами; 3-е – k3 способами;…; n-е - kn способами. И число способов, которыми можно выполнить каждое действие, не зависит от того, какие способы были выбраны для выполнения предшествующих действий. Тогда число способов, которыми можно выполнить все n действий, равно произведению k1 × k2 × k3 × ... × kn. Это и есть принцип умножения. Проще всего объяснить справедливость принципа умножения можно при помощи диаграммы (рис. 2).
Пример.
У человека имеется 3 рубашки (Р1, Р2, Р3), 2 галстука (Г1, Г2) и 2 пары ботинок (Б1, Б2). Он признает любое сочетание этих элементов. Сколькими способами он может одеться?
Решение.
Чтобы одеться, человек должен выполнить одно за другим и независимо одно от другого 3 действия:
1. Выбрать рубашку (три способа).
2. Выбрать галстук (два способа).
3. Выбрать ботинки (два способа).
Все способы выбора костюма показаны на диаграмме (рис. 2).


Рис. 2
Всего можно одеться 3 × 2 × 2 = 12 способами.
В2.2. Перестановки, размещения, сочетания
Определение. Перестановкой n данных элементовназывается любой упорядоченный набор этих элементов, место элемента в наборе имеет значение.
Пример 1.
Из трех элементов A,B,C можно составить шесть разных перестановок: ABC; ACB; CAB; CBA; BAC; BCA.
Число различных перестановок п элементов обозначается Рп. Выведем формулу подсчета числа Рп, для чего воспользуемся принципом умножения.
Чтобы определить перестановку n данных различных элементов, нужно выполнить одно за другим n действий:
· выбрать первый элемент перестановки (n способов);
· указать второй элемент (n - 1 способ);
…………………………………………;
· назвать последний элемент перестановки (1 способ).
Эти действия выполняются независимо одно от другого. В силу принципа умножения
Pn = n × (n - 1) ×...× 1 = n! (1)
Определение. Размещением, содержащим k различных элементов,выбранных из n имеющихся, называется любой упорядоченныйнабор k различных элементов, отобранных из n имеющихся различных элементов.
Пример 1.
Из букв A, B, C, D можно составить 12 размещений из двух букв:
AB; BA; AC; CA; AD; DA; BC; CB; BD; DB; CD; DC.
Число различных размещений обозначается символом 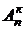 . Выведем формулу его подсчета.
. Выведем формулу его подсчета.
Чтобы составить размещение, нужно выполнить одно за другим и независимо одно от других k действий:
· назвать первый элемент размещения (n способов);
· указать второй элемент (n - 1 способ);
……………………………………………;
· назвать k-й, последний, элемент (n – k + 1 способов).
В соответствии с принципом умножения
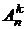 = n × (n – 1) ×...× (n – k + 1) =
= n × (n – 1) ×...× (n – k + 1) =
= 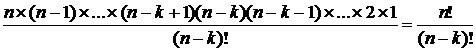 (2)
(2)
Пример 2. Сколько трех-, четырех-, пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 (0, 1, 2, 3, 4), если
a) повторения цифр запрещены;
b) повторения цифр разрешены.
Решение.
