Признаки сравнения рядов с положительными членами
Рассмотрим некоторые признаки, устанавливающие сходимость или расходимость рядов с положительными членами путём сравнения их с рядами, сходимость или расходимость которых известна.
Теорема 1 (I признак сравнения рядов с положительными членами). Пусть даны 2 ряда с положительными членами 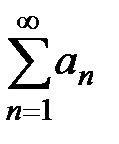 и
и 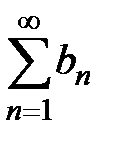 .
.
Если, начиная с некоторого номера N, для всех 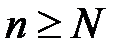 выполняется неравенство
выполняется неравенство 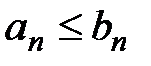 , тогда
, тогда
1) из сходимости ряда 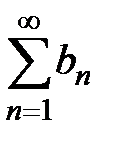 следует сходимость ряда
следует сходимость ряда 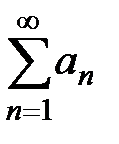 ,
,
2) из расходимости ряда 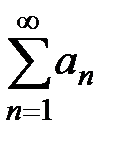 следует расходимость ряда
следует расходимость ряда 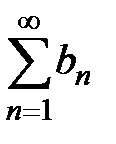 .
.
Доказательство. На основании того, что отбрасывание конечного числа членов (свойство 1, лекция 1, разд. 1.3) не влияет на сходимость или расходимость ряда, можно считать, не нарушая общности, что условие 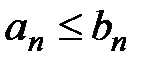 выполнено для всех
выполнено для всех 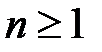 . Пусть
. Пусть 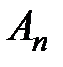 − частичная сумма ряда
− частичная сумма ряда 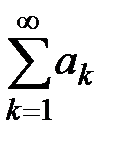 , а
, а 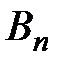 − частичная сумма ряда
− частичная сумма ряда 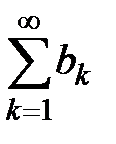 . По условию
. По условию 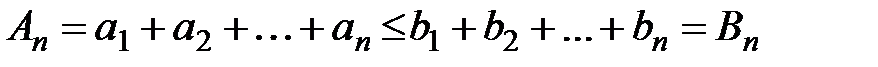 .
.
1) Если ряд 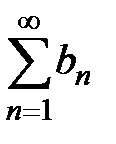 сходится, то последовательность
сходится, то последовательность 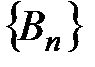 ограничена сверху, а значит, ограничена сверху и последовательность
ограничена сверху, а значит, ограничена сверху и последовательность 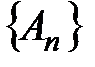 . Следовательно, по теореме 2 (лекция 1, разд. 1.4) о необходимом и достаточном условии сходимости ряда с положительными членами ряд
. Следовательно, по теореме 2 (лекция 1, разд. 1.4) о необходимом и достаточном условии сходимости ряда с положительными членами ряд 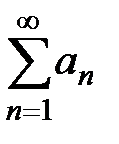 сходится, так как существует конечный предел последовательности
сходится, так как существует конечный предел последовательности 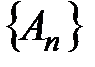 .
.
2) Если ряд 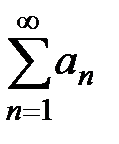 расходится, то последовательность
расходится, то последовательность 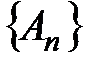 не ограничена, а значит, не ограничена и последовательность
не ограничена, а значит, не ограничена и последовательность 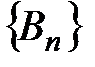 . Тогда по теореме 2 (лекция 1, разд. 1.4) ряд
. Тогда по теореме 2 (лекция 1, разд. 1.4) ряд 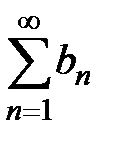 расходится. Теорема доказана.
расходится. Теорема доказана.
Пример 2. Исследовать на сходимость ряд 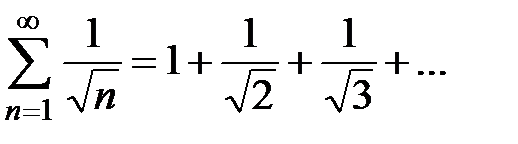 .
.
Решение. Обозначим 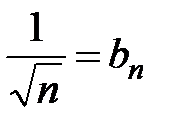 . Сравним ряд
. Сравним ряд 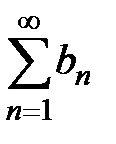 с гармоническим рядом
с гармоническим рядом 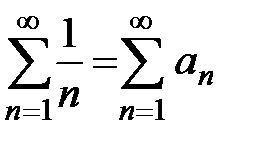 . При
. При 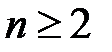
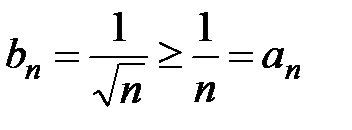 , а так как гармонический ряд
, а так как гармонический ряд
расходится, то расходится и ряд 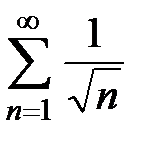 .
.
Ответ: ряд 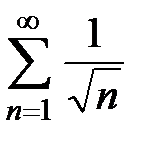 расходится.
расходится.
Пример 3. Исследовать на сходимость ряд 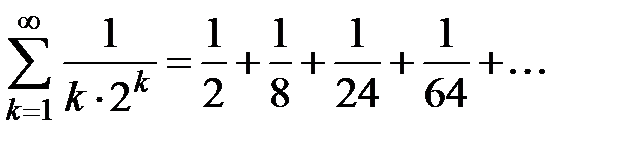 .
.
Решение. Обозначим 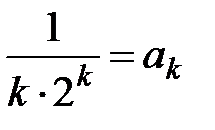 . Сравним данный ряд
. Сравним данный ряд 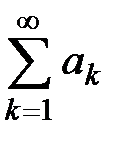 с рядом
с рядом
геометрической прогрессии 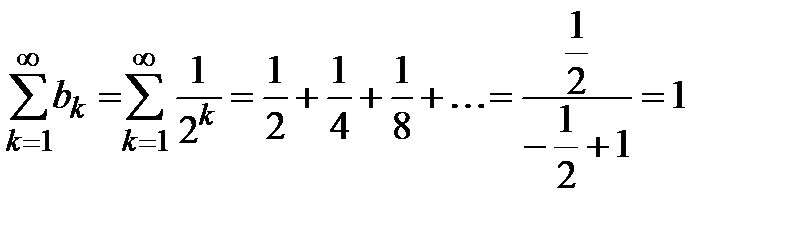 , который сходится, так как знаменатель прогрессии
, который сходится, так как знаменатель прогрессии 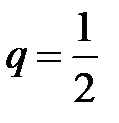 , то первые члены ряда равны, а при
, то первые члены ряда равны, а при 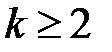 ,
, 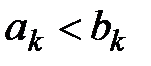 , значит, ряд
, значит, ряд 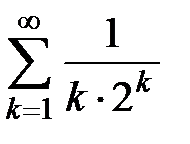 сходится по I признаку сравнения.
сходится по I признаку сравнения.
Ответ: ряд 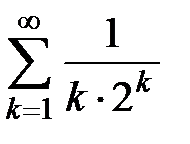 сходится.
сходится.
Теорема 2 (предельный признак сравнения рядов с положительными членами). Даны 2 ряда с положительными членами 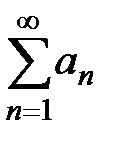 и
и 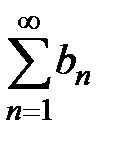 и пусть существует
и пусть существует 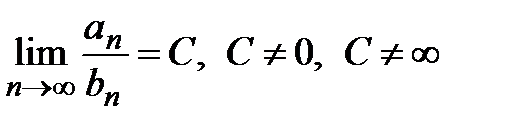 , тогда эти два ряда либо сходятся, либо расходятся одновременно.
, тогда эти два ряда либо сходятся, либо расходятся одновременно.
Доказательство. Так как по условию 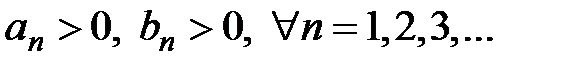 и
и 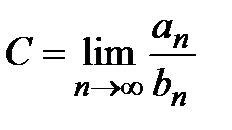 , то согласно свойству предела
, то согласно свойству предела 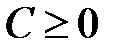 . По условию
. По условию 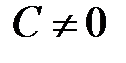 , значит,
, значит, 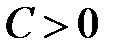 . По определению предела для всех
. По определению предела для всех 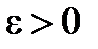 существует окрестность
существует окрестность 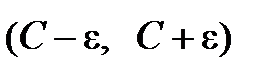 точки С такая, что
точки С такая, что 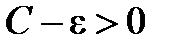 и существует такое натуральное число
и существует такое натуральное число 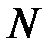 ,
,
зависящее от 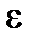 , что для всех
, что для всех 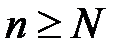 выполняется неравенство
выполняется неравенство 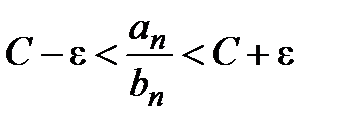 , или
, или 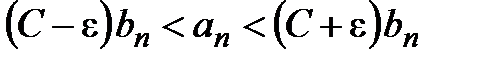 .
.
Если ряд 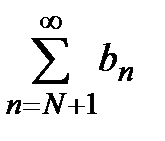 сходится, то сходится и ряд
сходится, то сходится и ряд 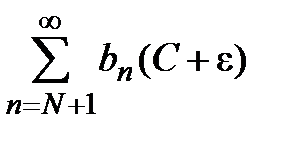 (свойство 2, лекция 1, разд. 1.3), откуда по I признаку сравнения рядов следует сходимость ряда
(свойство 2, лекция 1, разд. 1.3), откуда по I признаку сравнения рядов следует сходимость ряда 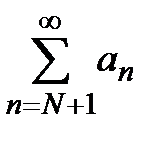 , так как
, так как 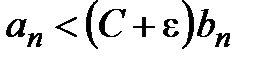 .
.
Если же ряд 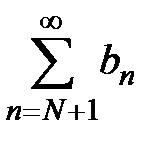 расходится, то расходится и ряд
расходится, то расходится и ряд 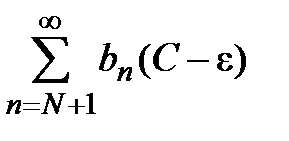 , а так как
, а так как 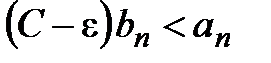 , то по I признаку сравнения рядов ряд
, то по I признаку сравнения рядов ряд 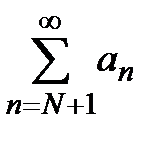 также расходится. Теорема доказана.
также расходится. Теорема доказана.
Замечание. Если 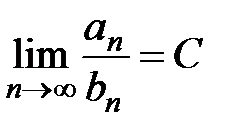 ,
, 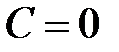 или
или 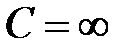 , то предельный признак не применим (теорема 2 в этих случаях не верна).
, то предельный признак не применим (теорема 2 в этих случаях не верна).
Пример 4. Исследовать на сходимость ряд 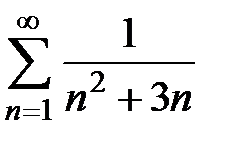 .
.
Решение. Обозначим 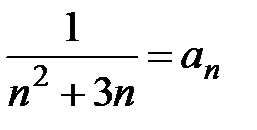 . Рассмотрим ряд
. Рассмотрим ряд 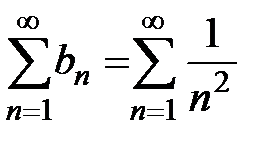 . Так как
. Так как
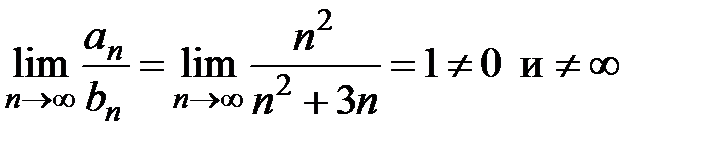 , то эти два ряда одновременно сходятся,
, то эти два ряда одновременно сходятся,
или расходятся (теорема 2). Поскольку 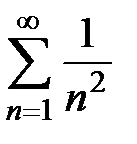 − ряд Дирихле с
− ряд Дирихле с 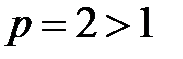
сходится, следовательно, исходный ряд 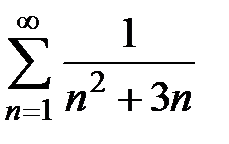 тоже сходится.
тоже сходится.
Ответ: ряд 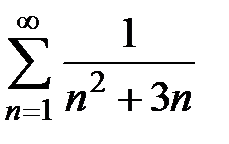 сходится.
сходится.
Пример 5. Исследовать на сходимость ряд 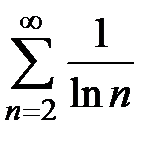 .
.
Решение. Обозначим 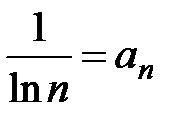 . Рассмотрим гармонический ряд
. Рассмотрим гармонический ряд 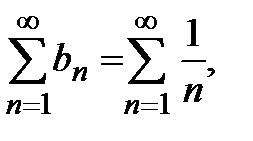 который расходится. Так как
который расходится. Так как 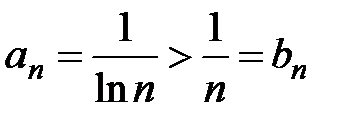
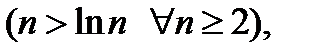 то по теореме 1 ряд
то по теореме 1 ряд 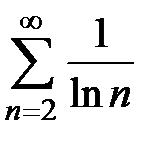 расходится.
расходится.
Ответ: ряд 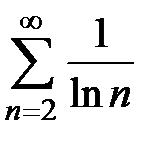 расходится.
расходится.
