Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства.

Рассмотрим непустое множество элементов, которые будем обозначать через x, y, z, … и множество действительных чисел. На этом множестве введем две операции (сложение и умножение). Пусть эти две операции подчиняются аксиомам:

1.

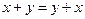
2.

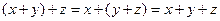
3.

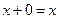
4.

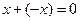
5.

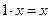
6.

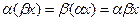
7.

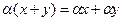
8.

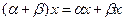
V; x, y, z, … 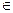V

Множество V с двумя операциями, удовлетворяющее аксиомам называется линейным пространством.

Элементы линейного пространства называются векторами, обозначаются 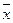, , 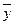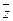. Существует единственный нулевой элемент, для каждого элемента существует единственный противоположный.

Линейная зависимость и независимость системы векторов. Пусть имеется n векторов.

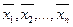
Составим линейную комбинацию:

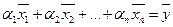
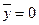, если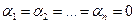 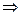система n векторов – линейно-зависима.

Если среди n векторов какие-то k линейно-зависимы, то вся система векторов является линейно-зависимой.

Если система n векторов линейно-независима, то любая часть из этих векторов будет тоже линейно-независимой.

Размерность и базис линейного пространства. Пусть система n векторов линейно-независима, а любая система n+1 векторов – линейно-зависима, тогда число n называют размерностью пространства. dimV=n

Система этих n линейно-независимых векторов называется базисом линейного пространства. Рассмотрим систему n+1 векторов.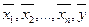

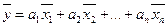
Такое представление называется разложение 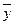по базису, а числа 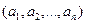называют координатами вектора.

Разложение любого вектора в выбранном базисе - единственно.

Матрица перехода от базиса к базису. Преобразование координат вектора при переходе к новому базису.

n – мерное пространство.

V_n – базис, состоящий из n векторов.

В пространстве есть базисы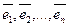

Введем матрицу перехода от 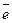к .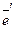

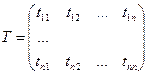
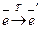
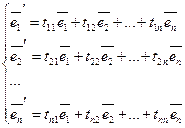
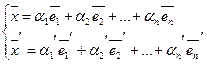
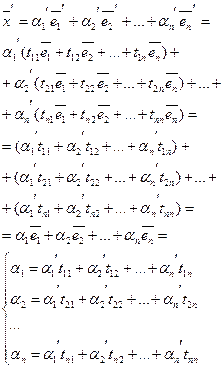
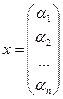
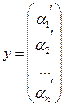
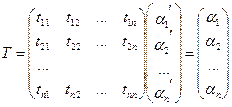
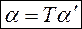
Евклидово пространство. Длина вектора. Угол между векторами.

Рассмотрим линейное пространство V, в котором уже есть 2 операции (сложение и умножение). В этом пространстве введем еще одну операцию. Она будет удовлетворять следующим аксиомам.

1.

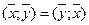
2.

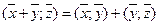
3.

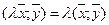
4.

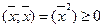
Указанная операция называется скалярным произведением векторов. N – мерное линейное пространство с введенной операцией скалярного произведения, называется Евклидовым пространством.

Длиной вектора называется арифметическое значение квадратного корня и скалярного квадрата.

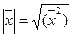
Длина вектора удовлетворяет следующим условиям:

1. 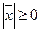, если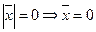

2.

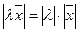
3. 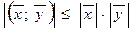- неравенство Коши-Буня

4. 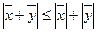- неравенство треугольника

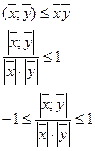
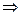
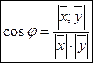
13.Скалярное произведение векторов и его свойства.

Скалярным произведениемдвух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.

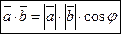
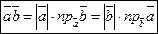
1.

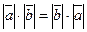
2.

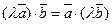
3.

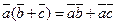
4.