Понятие производной и дифференциала

Определение.Производной функции 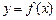в точке 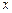называется предел отношения приращения функции 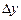к приращению аргумента 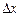при условии, что последнее стремится к нулю:

.

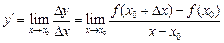Если этот предел конечный, то функция f(x) называется дифференцируемой в точке x_o; при этом она оказывается обязательно и непрерывной в этой точке.

Разберем смысл этого понятия. Учитывая смысл понятия предела, можно записать

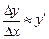или .

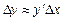Отсюда следует, что 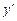является коэффициентом пропорциональности между приращением функции 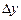и приращением аргумента 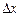, который показывает, как изменяется функция при изменении аргумента на единицу.

Механический смысл производной - это мгновенная скорость точки.

Геометрический смысл производной - это угловой коэффициент касательной к графику функции в точке с абсциссой .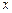

Если точка касания имеет координаты 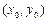, то уравнение касательной записывается в виде

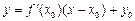
В общем случае, производная - это скорость изменения функции.

Нахождение производной называется дифференцированием функции. Производная функции находится с помощью таблицы основных производных (таблица 3.1) и основных правил дифференцирования.

Таблица 3.1 – Таблица производных основных элементарных функций

Функция	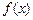Производная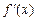

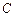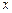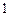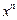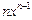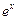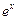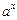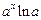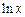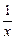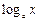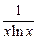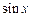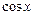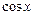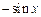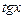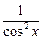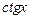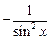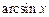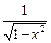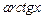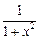Определение. Дифференциал функции – это главная линейная часть приращения функции

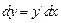
Приближенно дифференциал функции равен приращению функции

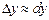
Пусть мы нашли для функции y=f(x) ее производную .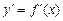

Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается 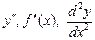. Механический смысл второй производной - это ускорение точки.

Аналогично определяется и обозначается производная третьего порядка - .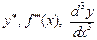

В общем случае определяется производная n-го порядка - .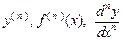

.

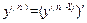Правила дифференцирования

Пусть функци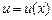и и 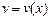имеют производные, тогда справедливы следующие правила.

1. Постоянный множитель можно вынести за знак производной.

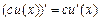
2. Производная алгебраической суммы функций равна алгебраической сумме производных этих функций:

.

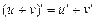3. Производная произведения двух функций находится по формуле:

.

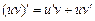4. Производная частного вычисляется по формуле:

.

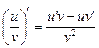5. Производная сложной функции 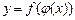, где 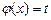находится по формуле

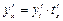
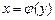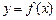6. Производная обратной функции , где и 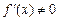находится по формуле

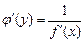
7. Производная функции 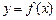заданной параметрическими уравнениями

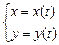
находится по формуле

.

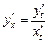Пример 3.1. Найти производные функций:

а) 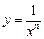; б) .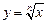

Решение.

Используя данные таблицы производных, получим:

а)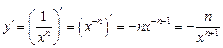

б)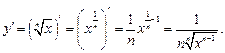

Пример 3.2. Найти производные функций:

а) 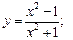б) .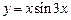

Решение.

Используя данные таблицы производных и правила производной частного и произведения, получим:

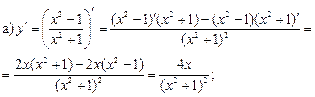
б) .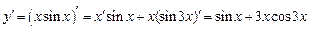

Пример 3.3.Найти производную сложной функции .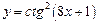

Решение.

Обозначим 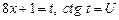, тогда получим .

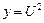Воспользуемся правилом производной сложной функции и таблицей производных, получим

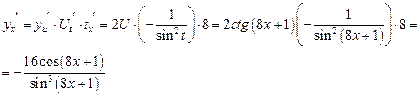
Пример 3.4. Пользуясь правилом дифференцирования обратной функции, найти производную 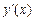для функции .

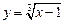Решение.Обратная функция 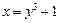имеет производную 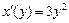. Следовательно,

.

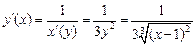Пример 3.5. Найти производную функции 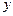заданной уравнением .

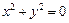Решение.Продифференцируем уравнение по х, рассматривая при этом у как функцию х.

.

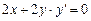Выразим из полученного уравнения 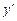, получим

.

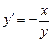Пример 3.6.Найти производную функции заданной системой

.

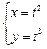Решение.По правилу производной функции заданной параметрическими уравнениями находим

.
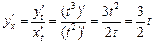