Понятие дифференциала числовой функции

Определение. Если числовая функция 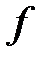дифференцируема в точке 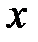, то ее

дифференциалом 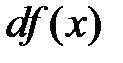в этой точке называют однородную линейную функцию

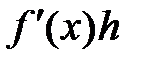(новой) независимой переменной .

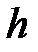Таким образом,

=

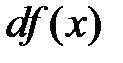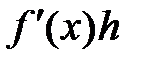
Положив в формуле 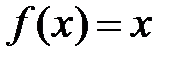, получим

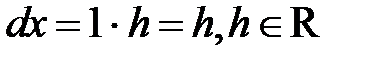
так что дифференциал 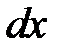функции 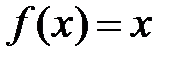в каждой точке 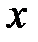есть

тождественная функция. Получаем

=

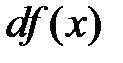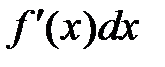
равенство двух линейных функци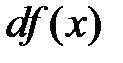й и 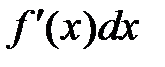. Из него следует, что часто используемое обозначение производной 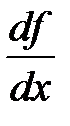можно рассматривать, как отношение дифференциалов

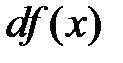и .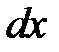

Функция 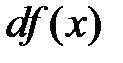определена для всех действительных значений .

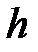Однако по традиции часто рассматривают 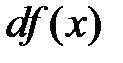лишь на множестве тех ,

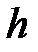для которых 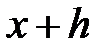принадлежит области определения функции; т.е.,

лишь на множестве приращений аргумента 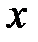функции .

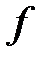Это объясняется тем, что дифференциал тесно связан с приращением функции.

Так как, по предположению, 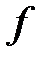дифференцируема в точке x, то

,

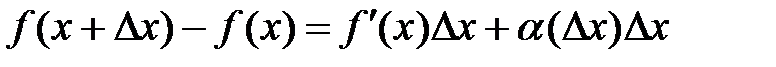где 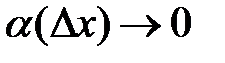при 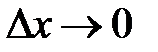и первое слагаемое в правой части дифференциал,

но рассматриваемый только для 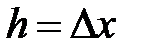. Если 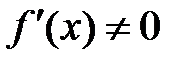, то

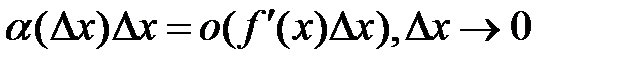,поэтому говорят, что «дифференциал есть главная

линейная часть приращения функции».

Геометрический и механический смысл дифференциала.

Пусть числовая функция 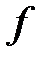дифференцируема в точке 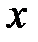. Как известно, ее график

имеет в точке 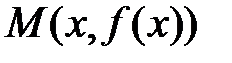касательную с угловым коэффициентом .

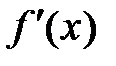ТеоремаЗначение 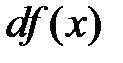= 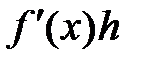дифференциала равно приращению ординаты этой

касательной при переходе от 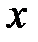к .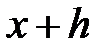

Инвариантность формы первого дифференциала

Правило дифференцирования сложной функции приведет нас к одному замечательному и важному свойству дифференциала.

Пусть функци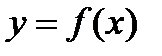и и 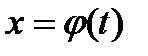таковы, что из них может быть составлена сложная функция: 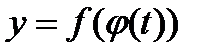. Если существуют производные 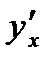и 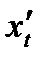, то существует и производная

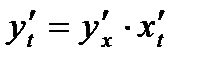
Перейдём теперь к независимой переменной 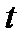; в этом предположении имеем другое выражение для дифференциала:

.

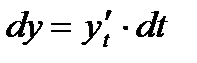Заменяя производную 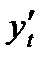её выражением и замечая, что 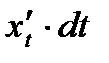есть дифференциал 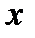как функции от 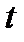, окончательно получим:

,

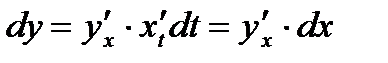т. е. вернёмся к прежней форме дифференциала.

Таким образом, мы видим, что

форма дифференциала может быть сохранена даже в том случае, если прежняя независимая переменная заменена новой.

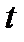Мы всегда имеем право писать дифференциал как в форме (1), будет ли независимой переменной или нет; разница лишь в том, что, если за независимую переменную выбрано , то 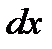означает не произвольное приращение 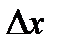, а дифференциал 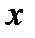как функции от 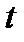. Это свойство и называют инвариантностью формы дифференциала.

Дифференциал суммы, произведения и частного функций.

Из любой формулы для производной в точке x при умножении на dx

получается соответствующая формула для дифференциала. В частности, в точках,

где функции u, v удовлетворяют условиям теорем о дифференцируемости суммы,

произведения или частного получаем: d(u+v)=du+dv;

аналогично, d(uv)=vdu+udv, d(u/v)=(vdu-udv)/v².

Отметим, что если C – постоянная, то dC=0, dCu=Cdu.