Понятие дифференциала и его геометрический смысл
Пусть функция 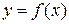 определена на промежутке
определена на промежутке 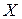 и дифференцируема в окрестности точки
и дифференцируема в окрестности точки 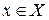 ,тогда
,тогда 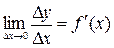 или по теореме о связи бесконечно малых с пределами функций имеем
или по теореме о связи бесконечно малых с пределами функций имеем 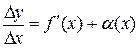 , где
, где 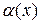 - бесконечно малая величина при
- бесконечно малая величина при 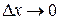 . Отсюда:
. Отсюда: 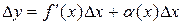 . Таким образом, приращение функции
. Таким образом, приращение функции 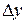 состоит из двух слагаемых: 1.
состоит из двух слагаемых: 1. 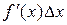 - линейного относительно
- линейного относительно 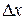 , т.к.
, т.к. 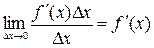 ; 2.
; 2. 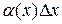 - нелинейного относительно
- нелинейного относительно 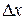 , т.к.
, т.к. 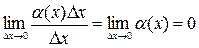 .
.
Дифференциалом функции называется главная, линейная относительно 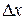 часть приращения функции, равная произведению производной на приращение независимой переменной:
часть приращения функции, равная произведению производной на приращение независимой переменной: 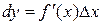 .
.
Пример. Найти приращение функции 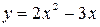 при
при 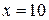 и
и 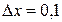
Пример. Найти дифференциал функции 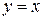 .
.
Дифференциал независимой переменной 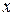 равен приращению этой переменной:
равен приращению этой переменной: 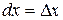 .
.
Тогда формулу для дифференциала функции можно записать в виде: 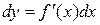 . Откуда
. Откуда 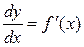 , поэтому
, поэтому 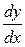 можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем
можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем 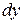 и знаменателем
и знаменателем 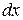 .
.
Геометрический смысл.На графике функции 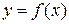 (рис. 5.) возьмем произвольную точку
(рис. 5.) возьмем произвольную точку 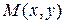 . Дадим аргументу
. Дадим аргументу 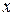 приращение
приращение 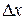 , тогда функция получает приращение
, тогда функция получает приращение 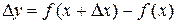 . В точке
. В точке 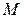 проведем касательную, образующую угол
проведем касательную, образующую угол 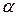 с осью
с осью 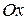 . Из
. Из 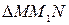 видно, что
видно, что 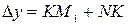 . Из
. Из 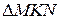 имеем:
имеем: 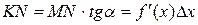 . Таким образом,
. Таким образом, 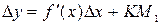 и соответствует формуле
и соответствует формуле 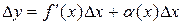 .
.
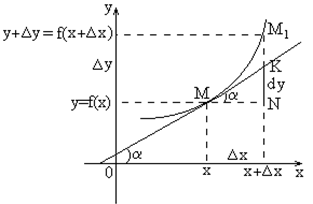
Рис. 5.
Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции 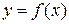 в данной точке, когда
в данной точке, когда 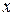 получает приращение
получает приращение 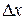 .
.
Свойства дифференциала аналогичны свойствам производной:
1) 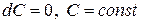 . . | 4) 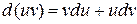 . . |
2) 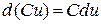 . 3) . 3) 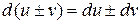 . . | 5) 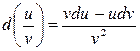 . . |
Формула дифференциала не изменится, если вместо функции от независимой переменной 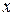 рассматривать функцию от зависимой переменной
рассматривать функцию от зависимой переменной 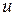 . Это свойство дифференциала получило название инвариантности (т.е. неизменности) формы дифференциала, т.е.
. Это свойство дифференциала получило название инвариантности (т.е. неизменности) формы дифференциала, т.е. 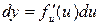 .
.
Приближенные вычисления с помощью дифференциала.Согласно формулы 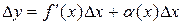 , т.е.
, т.е. 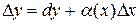 , при достаточно малых значениях
, при достаточно малых значениях 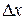 приращение функции
приращение функции 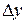 приблизительно равно ее дифференциалу
приблизительно равно ее дифференциалу 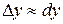 ,
, 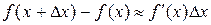 . Эту формулу часто используется в приближенных вычислениях.
. Эту формулу часто используется в приближенных вычислениях.
Пример. Вычислить 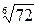 .
.
