Указания по технике безопасности. При выполнении работы студенты должны руководствоваться общими для учебных аудиторий правилами техники безопасности.

При выполнении работы студенты должны руководствоваться общими для учебных аудиторий правилами техники безопасности.

Методика и порядок выполнения работы

Получить вариант задания (таблица 7.1).

Порядок выполнения рассмотрим на примере.

Пример. Решить задачу линейного программирования симплекс - методом. Для нахождения опорного плана использовать метод искусственных переменных.

Ограничения:

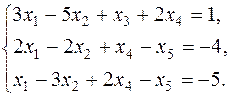
Целевая функция:

.

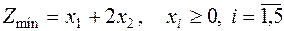В базис можно выделить переменную 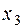. Введем две искусственные переменные 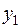и .

;

.

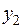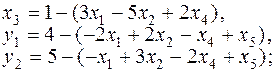
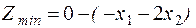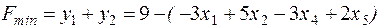Составим первую симплекс- таблицу:

Свободные Базисные	Свобод­ный член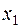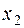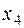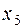
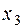			-5
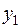		-2		-1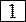
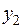		-1		-2
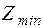		-1	-2
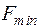		-3		-3

Наименьший положительный элемент в строке линейной формы 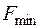равен 2. Разрешающий элемент находится на пересечении столбца переменной 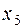и строки переменной .

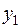Заполним следующую симплекс - таблицу:

Свободные Базисные	Свободный член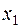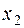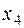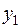
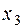			-5
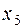		-2		-1
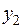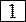				-1	-1
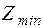		-1	-2
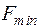				-1	-2

Наименьший положительный элемент в строке линейной формы 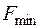равен 1. Минимальное симплекс - отношение соответствует строке переменной .

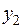Заполним следующую симплекс - таблицу:

Свободные Базисные	Свобод­ный член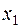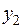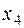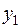
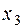				-3
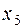		-4	-2
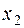				-1	-1
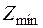				-2	-1
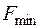			-1		-1

Так как 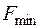=0, а 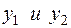переведены в число свободных, переход к первому опорному решению завершен. Строку, соответствующую 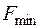, и столбцы переменных 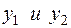вычеркиваем в последней таблице и перепишем ее в новом виде:

Свободные Базисные	Свободный Член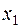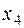
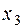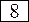			-3
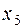		-4
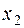			-1
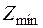			-2

Решим задачу для исходной линейной формы 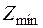. В последней таблице находим разрешающий элемент - он равен 8. Выполняя действия согласно алгоритму симплекс - метода, получим следующую таблицу:

Свободные Базисные	Свободный член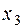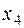
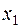	6/8	1/8	-3/8
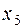		4/8	-12/8
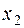	2/8	-1/8	-5/8
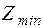	10/8	-1/8	-13/8

В последней строке ( 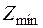) положительных элементов нет, следовательно, оптимальное решение найдено.

Значение целевой функции 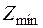равно 10/8. Оптимальный план 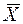=(6/8; 2/8; 0; 0; 5).

Содержание отчета и его форма

Отчет должен содержать:

6.1 Задачу приведенную к виду, допускающему применение симплекс-алгоритма;

6.2 Симплекс-таблицу;

6.3 Оптимальное решение;

6.4 Выводы.

Контрольные вопросы и защита работы

7.1В каком случае применяется метод искусственного базиса?

7.2 Как анализируются варианты решения задачи линейного программирования при использовании метода искусственного базиса?

7.3 Чем определяется количество вводимых искусственных переменных?

Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.

Практическое занятие 20, 21.

Моделирование движения транспортных средств на регулируемых перекрестках

Цель и содержание

Цель работы – приобрести навыки моделирование движения транспортных средств на регулируемых перекрестках.

В результате выполнения работы студенты должны:

1. Определить интенсивность обслуживания.

2. Определить среднее число находящихся в системе заявок на обслуживание.

3. Определить среднюю продолжительность пребывания заявки в системе.

4. Определить среднее число заявок в очереди на обслуживание.

5. Определить среднюю продолжительность пребывания автомобиля в очереди.

6. Сделать выводы.

Теоретическое обоснование

Одним из способов моделирования движения транспортных средств на перекрестках (и не только) является применение метода теории массового обслуживания.

Перекресток, имеющий светофорное регулирование, не сложно представить как одноканальную (или многоканальную) систему массового обслуживания с неограниченным временем ожидания, где:

1. Интенсивность заявок 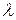– интенсивность движения транспортных средств n, авт/с;

2. Дисциплина очереди – первый пришел – первый обслуживаешься;

3. Четкий механизм обслуживания – при структуре цикла регулирования:

,

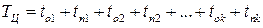(4.1)

интенсивность обслуживания определится:

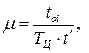авт/с,

(4.2)

где 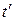– время обслуживания одного автомобиля, с;

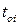– продолжительность разрешающего сигнала для i-го направления, с.

Время обслуживания автомобиля зависит от комплексного показателя.

Стационарный режим функционирования данной системы массового обслуживания (СМО) существует при 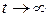для любого n = 0, 1, 2, ... и когда 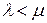. Система алгебраических уравнений, описывающих работу данной СМО имеет вид:

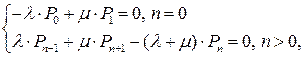(4.3)

где 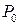– вероятность того, что перекресток свободен для движения и заявок не поступает,

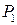– вероятность того, что перекресток обслуживает один автомобиль, очереди нет,

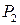– вероятность того, что перекресток обслуживает один автомобиль, очередь – один автомобиль,

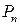– вероятность того, что перекресток обслуживает один автомобиль, очередь – 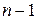автомобилей.

Решение данной системы уравнений имеет вид:

,

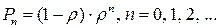(4.4)

где .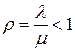

Характеристики данной СМО следующие:

Среднее число находящихся в системе заявок на обслуживание:

.

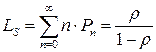(4.5)

Средняя продолжительность пребывания заявки в системе:

.

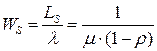(4.6)

Среднее число заявок в очереди на обслуживание:

.

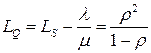(4.7)

Средняя продолжительность пребывания автомобиля в очереди:

.

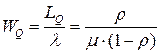(4.8)

Аппаратура и материалы

Микрокалькулятор, программное обеспечение MS Excel.