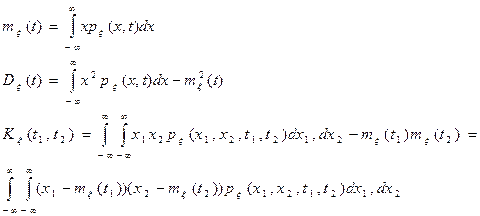Удовлетворяющее условиям 1-6. Тогда существует вероятностное пространство и случайный процесс такие, что семейство конечномерных распределений СП совпадает с .
Теорема Колмогорова показывает, что условия 1-6 являются необходимыми и достаточными для существования процесса с заданными конечномерными распределениями 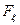 .Таким образом, всегда найдется СП с заданным семейством конечномерных распределений. Более того, в общем случае такой процесс будет не единственным. Т.е. семейство конечномерных распределений задает целый класс случайных процессов, которые в некотором смысле являются эквивалентными.
.Таким образом, всегда найдется СП с заданным семейством конечномерных распределений. Более того, в общем случае такой процесс будет не единственным. Т.е. семейство конечномерных распределений задает целый класс случайных процессов, которые в некотором смысле являются эквивалентными.
СП  и
и 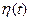 , определенные на одном и том же множестве Т и в одном и том же вероятностном пространстве
, определенные на одном и том же множестве Т и в одном и том же вероятностном пространстве 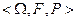 и принимающие значения в одном и том же измеримом пространстве, называются стохастически эквивалентными, если они совпадают почти наверное при любом фиксированном t:
и принимающие значения в одном и том же измеримом пространстве, называются стохастически эквивалентными, если они совпадают почти наверное при любом фиксированном t: 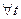
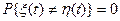 .
.
Согласно общему духу ТВ, пренебрегающей событиями с Р=0 , считается что можно заменить изучение одного СП стохастически эквивалентным.
Моментные характеристики СП [1,4]
Раздел теории СП, занимающийся только моментами первых двух порядков, называется корреляционной теорией.
Для характеристики СВ были определены неслучайные числовые характеристики – матожидание 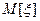 - среднее значение СВ; дисперсия
- среднее значение СВ; дисперсия 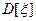 - разброс значений относительно
- разброс значений относительно 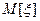 ; корреляционный (ковариационный) момент
; корреляционный (ковариационный) момент 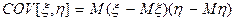 , который характеризует степень линейной зависимости между СВ
, который характеризует степень линейной зависимости между СВ 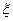 и
и 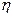 .
.
Так как сечения СП представляют собой СВ, мы можем определить основные моментные характеристики СП. Моментные характеристик СП задают его простейшие свойства и вычисляются с помощью конечномерных распределений различных порядков.
Пусть  - действительный скалярный процесс. Неслучайная функция
- действительный скалярный процесс. Неслучайная функция 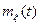 ,
, 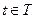 , которая
, которая 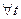 равна матожиданию соответствующего сечения СП
равна матожиданию соответствующего сечения СП 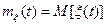 , называется матожиданием СП. Его можно найти через одномерный закон распределения.
, называется матожиданием СП. Его можно найти через одномерный закон распределения.
Если 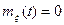
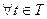 , то СП называется центрированным. Центрированный СП можно получить
, то СП называется центрированным. Центрированный СП можно получить 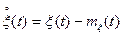 . Реализации
. Реализации 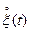 - отклонения от 0.
- отклонения от 0.
Дисперсия СП – это неслучайная функция СП, которая при каждом t равна дисперсии соответствующего сечения. 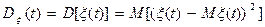 - можно найти через одномерный закон распределения.
- можно найти через одномерный закон распределения.
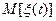 и
и 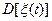 важны, но не характеризуют внутреннюю структуру процессов.
важны, но не характеризуют внутреннюю структуру процессов.
Неслучайная функция
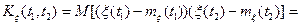
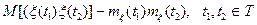 называется корреляционной функцией СП.
называется корреляционной функцией СП.
Т.е. корреляционная функция – функция двух аргументов - для каждой пары чисел 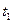 и
и 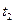 равна корреляционному моменту соответствующих сечений и характеризует степень их линейной зависимости. Для расчёта корреляционной функции необходимо знать двумерное распределение.
равна корреляционному моменту соответствующих сечений и характеризует степень их линейной зависимости. Для расчёта корреляционной функции необходимо знать двумерное распределение.
Если распределения 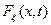 и
и 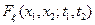 имеют плотности распределения, то
имеют плотности распределения, то