Уравнение прямой с угловым коэффициентом

Аксиомы стереометрии

• На каждой прямой и в каждой плоскости имеются, по крайней мере, две точки.
• В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
• Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
• Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
• Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
• Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
• Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;
2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
• Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

Точка

В геометрии, топологии и близких разделах математики то́чкой называют абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни каких-либо других измеримых характеристик. Таким образом, точкой называют нуль мерный объект. Точка является одним из фундаментальных понятий в математике; любая геометрическая фигура считается состоящей из точек.

Прямая

Пряма́я — одно из фундаментальных понятий геометрии.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Согласно примеру Д. Гильберта («точкой можно назвать хоть стул»), может обозначать достаточно произвольные объекты, даже изображение которых будет зависеть от выбранной аксиоматики и/или модели геометрии. Например, в модели Пуанкаре геометрии Лобачевского прямыми являются полуокружности.

Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени

Свойства

• Через любые две несовпадающие точки можно провести единственную прямую.
• Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
• В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
• прямые пересекаются;
• прямые параллельны;
• прямые скрещиваются.
• Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

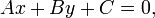
где 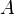, 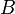и 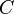— произвольные постоянные, причем постоянные 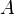и 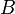не равны нулю одновременно. Вектор с координатами 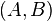называется нормальным вектором, он перпендикулярен прямой.

При 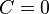прямая проходит через начало координат. Также уравнение можно переписать в виде

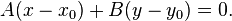
Уравнение прямой с угловым коэффициентом

Уравнение прямой линии, пересекающей ось 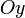в точке 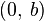и образующей угол 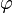с положительным направлением оси :

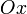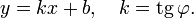
Коэффициент 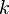называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси