Задача 1 задача 2 задача 3 задача 4

Задача 1 - Жестко соединенная конструкция из легкого стержня и небольшого по размерам шарика массой m может совершать колебания в вертикальной плоскости под действием пружины k, двигаясь при вращении без трения вокруг горизонтальной оси О. Пружина легкая, точка прикрепления ее к стержню делит его длину в отношении 1:2, считая от шарика. В положении равновесия шарик горизонтален, а ось пружины вертикальна. Найдите удлинение пружины в положении равновесия системы. Найдите период малых колебаний конструкции.

Задача 2 - Жестко соединенная конструкция из легкого стержня и небольшого по размерам шарика массой m может совершать колебания под действием двух пружин жесткостью k₁ и k₂, двигаясь при вращении без трения вокруг вертикальной оси О по гладкой поверхности стола. Пружины легкие, их оси горизонтальны, а точки прикрепления их к стержню делят его на три равные части. В положении равновесия оси пружин перпендикулярны

стержню, и пружина жесткостью k₁ растянута на величину L₁. Найдите деформацию второй пружины в положении равновесия. Найдите период малых колебаний конструкции.

Задача 3 - Металлический прут в форме дуги окружности радиусом L висит на двух легких нитях длиной L каждая. Масса прута равна m, его поперечное сечение постоянно. Угол между нитями 2b. Найдите силу натяжения нитей в положении равновесия. Найдите период малых колебаний такой «дуги» в вертикальной плоскости, совпадающей с плоскостью «дуги».

Задача 4 - Как изменится частота колебаний математического маятника, представляющего собой груз на легкой пружине, если к середине стрежня прикрепить горизонтальную пружину жесткости k?

Дифференцируем закон сохранения механической энергии

Задача 1 - Получите дифференциальное уравнение гармонических колебаний для уже исследованных и знакомых Вам колебательных систем: горизонтального и вертикального пружинногомаятников, математического маятника. Убедитесь в том, что в рассматриваемых ситуациях это равноценный математический прием.

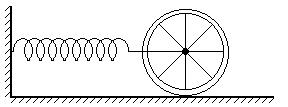
Задача 2 - Пружина жесткостью k одним концом присоединена к оси колеса массы m, которое способно катиться без проскальзывания, а другим концом присоединена к стенке. Какова частота колебаний системы? Масса колеса однородно распределена по ободу.

Задача 3 - К ободу колеса с горизонтально расположенной осью прикрепили грузик массы m. Найдите массу колеса, предполагая ее однородно распределенной по ободу, если частота малых колебаний колеса с грузиком вокруг оси равна W, а его радиус равен R. (МГУ)

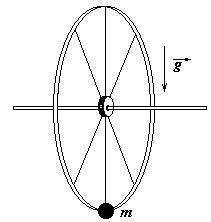
Задача 4 - Найдите частоту колебаний тонкого обруча радиуса R, подвешенного на гвозде. Проскальзывания нет; колебания происходят в плоскости обруча.

Колебательные системы

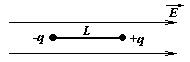1 Жесткий диполь, длина которого L и концевые заряды q, помещен в однородное электрическое поле напряженностью Е. Определите период малых колебаний диполя в электрическом поле. Масса каждого из концевых зарядов m.

2 Бусинка массой m с зарядом q может двигаться без трения по натянутой нити длины 2L, на концах которой закреплены заряды Q. Найдите период малых колебаний бусинки относительно положения равновесия.

3 В модели атома Томсона предполагалось, что положительный заряд q, равный по модулю заряду электрона, равномерно распределен внутри шара радиусом R. Чему равен период колебаний (внутри шара, вдоль его диаметра) электрона, помещенного в такой шар? Масса электрона m.

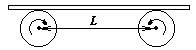4 Доска массы m лежит на двух катках, вращающихся с большой угловой скоростью навстречу друг другу. Расстояние между осями катков L, коэффициент трения скольжения доски по катку m. Найдите частоту продольных колебаний доски.

5 Определите период малых колебаний ртути массы m = 200 г, налитой в U-образную трубку сечения S = 0,50 см². Плотность ртути r = 13,6×10 кг/м³.

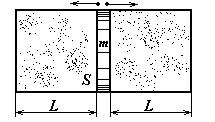
6 Найдите период малых колебаний поршня массы m, разделяющего гладкий горизонтальный цилиндрический сосуд сечения S на две части длины L каждая. По обе стороны поршня находится га при давлении p₀ и температуре Т₀. При колебании поршня температура газа не меняется.

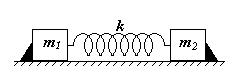
7 Два грузика, скрепленные пружиной жесткости k, находятся на гладкой горизонтальной поверхности. Пружину сжимают и удерживают в деформированном состоянии двумя упорами. Упоры убирают.. Найдите период колебаний, которые возникнут в системе.

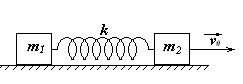8 Два грузика, скрепленные пружиной жесткости k, находятся на гладкой горизонтальной поверхности. Пружина не деформирована. Толчком одному из грузов сообщают скорость v₀. Опишите дальнейшее поведение системы. Найдите максимальную деформацию пружины.

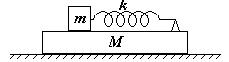9 Тело массы m скреплено пружиной жесткости k с бруском массы M. Пружину сжимают, удерживая тела в неподвижном состоянии, а затем освобождают. Определите периоды колебаний Т₁ и Т₂ тела и бруска.

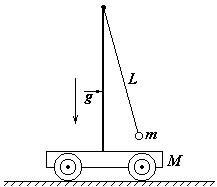
10 На гладкой горизонтальной поверхности находится тележка массы М с установленным на ней математическим маятником длины L и массы m. Найдите период колебаний системы.

11 Найдите отношение частот колебаний молекулы Н₂ и молекулы НD (D – атом дейтерия).

12 В системе из задачи 1 убирают один из упоров (допустим, правый). Как будет зависеть от времени величина деформации пружины? Начальная деформация пружины DL.
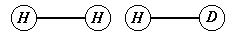