Свойства операций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A')'=A

(λA)'=λ(A)'

(A+B)'=A'+B'

(AB)'=B'A'

Виды матриц

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

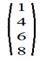
5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

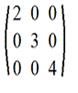
6. Единичная матрица: m=n и

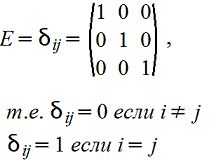
7. Нулевая матрица: a_ij=0, i=1,2,...,m

j=1,2,...,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симметрическая матрица:m=n и a_ij=a_ji(т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательноA'=A

Например,

10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=jимеем a_ii=-a_ii)

Пример.

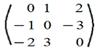
· Ясно,A'=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji- комплексно - сопряженное к a_ji, т.е. если A=3+2i, то комплексно - сопряженное Ã=3-2i)

Пример

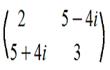
9. Обратная матрица. Определение.

10. Вычисление обратной матрицы.

Алгоритм вычисления обратной матрицы

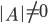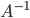1. Находим определитель исходной матрицы. Если , то существует.

2. Находим транспонированную матрицу .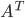

3. Находим алгебраические дополнения элементов транспонированной матрицы 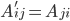и составляем из них присоединённую матрицу 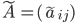, где 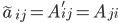(i,j=1,…,n).

4. Вычисляем обратную матрицу по формул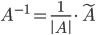е где .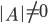

5. Проверяем правильность вычисления обратной матрицы 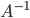, исходя из определения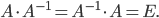

Пример:

Задача:Найти матрицу обратную к матрице

Решение:

1.

Следовательно 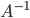, существует.

2.

3.

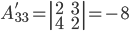
Т.е. присоединённая матрица имеет вид:

4. Выписываем обратную матрицу по формуле:

Полученная обратная матрица имеет вид:

11. Ранг матрицы. Определение.

Ранг матрицы. Определение.
Рангом системы строк (столбцов) матрицы
А с m строк и n
столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков всевозможных ненулевых миноров этой матрицы. Если все миноры равны нулю, то ранг тоже равен нулю.
Ранг матрицы — Размерность образа dim(im(A))
линейного оператора, которому соответствует матрица.
Обычно ранг матрицы
A обозначается rang A,rg A или rank A.

12. Вычисление ранга матрицы.