Свойства линейных операций над матрицами
1. А + В = В + А; 2. А + (В + С) = (А + В) + С;
3. А + 0 = А (0 – нулевая матрица); 4. А – В = А + (– 1) ∙ В;
5. А + (– А) = 0; 6. 1 ∙ А = А;
7. (α + β) А = αА + βВ; 8. α(А + В) = αА + αВ;
9. α(βА) = (αβ)А, где А, В, С – матрицы, α и β – скаляры (любые действительные числа)
● Под элементарными преобразованиями матриц понимают следующие действия:
1) умножение всех элементов какой-либо строки (или столбца) на действительное число λ ¹ 0;
2) прибавление к элементам какой-либо строки (или столбца) величин, пропорциональных элементам другой строки (или столбца) (замена элементов строки (столбца) линейными комбинациями соответствующих элементов других строк (столбцов);
3) перестановку местами двух строк (или столбцов).
Матрицы называются эквивалентными, если одна может быть получена из другой с помощью элементарных преобразований.
● Если в прямоугольной матрице 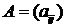 , размера n ´ m выделим k столбцов и k строк, причем k не больше наименьшего из чисел m и n и составим определитель из элементов, стоящих на пересечении выбранных строк и столбцов, то полученные указанным способом определители называются минорами матрицы А. Наивысший возможный порядок минора прямоугольной матрицы размера n ´ m равен наименьшему из чисел m и n. Для квадратной матрицы размера n наибольший возможный порядок минора равен n.
, размера n ´ m выделим k столбцов и k строк, причем k не больше наименьшего из чисел m и n и составим определитель из элементов, стоящих на пересечении выбранных строк и столбцов, то полученные указанным способом определители называются минорами матрицы А. Наивысший возможный порядок минора прямоугольной матрицы размера n ´ m равен наименьшему из чисел m и n. Для квадратной матрицы размера n наибольший возможный порядок минора равен n.
● Определение. Матрица имеет ранг r, если среди ее миноров существует хотя бы один, отличный от нуля, минор порядка r, а все миноры порядка r + 1 и выше равны нулю или не существуют.
Ранг нулевой матрицы считается равным нулю.
Пример. Для квадратной матрицы 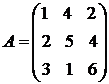 порядка n = 3 ее ранг r £ 3. Поскольку
порядка n = 3 ее ранг r £ 3. Поскольку 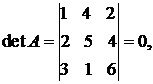 но, например, составленный из элементов этой матрицы минор
но, например, составленный из элементов этой матрицы минор 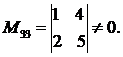 Размерность этого минора равна 2, следовательно, ранг данной матрицы r = 2. Однако этот способ определения ранга матрицы не всегда прост. Удобнее привести данную матрицу А к так называемой ступенчатой форме, что возможно с помощью элементарных преобразований. Матрица ступенчатой формы
Размерность этого минора равна 2, следовательно, ранг данной матрицы r = 2. Однако этот способ определения ранга матрицы не всегда прост. Удобнее привести данную матрицу А к так называемой ступенчатой форме, что возможно с помощью элементарных преобразований. Матрица ступенчатой формы 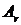 такова, что все «диагональные» элементы
такова, что все «диагональные» элементы 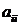 , где
, где 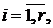 отличны от нуля, а все элементы, расположенные под этой диагональю, равны нулю:
отличны от нуля, а все элементы, расположенные под этой диагональю, равны нулю:
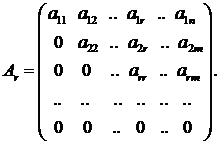
Число r элементов 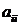 стоящих на главной диагонали, не зависит от способа приведения прямоугольной матрицы А к виду ступенчатой матрицы Аr и называется рангом матрицы А.
стоящих на главной диагонали, не зависит от способа приведения прямоугольной матрицы А к виду ступенчатой матрицы Аr и называется рангом матрицы А.
Следствие. Ранги двух эквивалентных матриц равны.
● Операция над матрицей 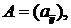 при которой ее строки становятся столбцами с теми же номерами, а столбцы – строками, называется транспонированием. Обозначается транспонированная матрица
при которой ее строки становятся столбцами с теми же номерами, а столбцы – строками, называется транспонированием. Обозначается транспонированная матрица 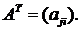
Операция транспонирования обладает следующими свойствами:
1. 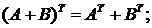 2.
2. 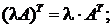
3. 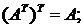 4.
4. 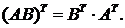
● Произведение матрицы А на матрицу В определяется только в случае, если число столбцов матрицы А равно числу строк матрицы В.
В этом случае матрицы А и В называются согласованными.
Замечание. Из того что матрица А согласована с В, а значит существует матрица АВ, не следует что матрицу В можно умножить на А, т. к. из согласованности А с В не следует согласованность В с А. Следовательно,
в общем случае АВ ¹ ВА. Однако АЕ = ЕА.
Действие умножения матриц выполняется по принципу «строка на столбец», что схематично представлено на рис. 24.
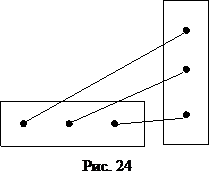 Произведением матрицы
Произведением матрицы 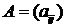 на матрицу
на матрицу 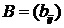 называется такая матрица
называется такая матрица 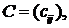 элементы которой
элементы которой 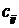 равны сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:
равны сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В: 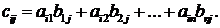
Примеры. Найти АВ и ВА, если:
1) 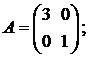
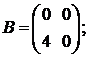 2)
2) 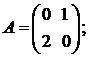
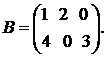
Решение. 1) А согласована с В и В согласована с А, значит, существуют матрицы АВ и ВА:
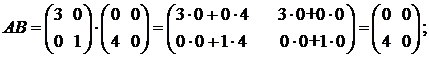
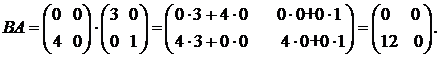
Итак, существуют матрицы АВ и ВА, однако АВ ¹ ВА.
2) Матрица А с В согласована, значит существует АВ:
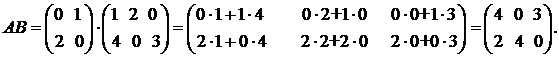
Но матрица В не согласована с А, следовательно, произведение матриц ВА не существует.
Свойства умножения матриц
1. (АВС) = А(ВС); 2. А(lВ) = l(АВ) = (lА)В;
3. (А + В)С = АС + ВС; 4. С(А + В) = СА + СВ;
5. АЕ = ЕА = А, где Е – единичная матрица; 6. А0 = 0А = 0.
7. det (АВ) = det А det В, т. е. определитель произведения квадратных матриц равен произведению их определителей.
ОБРАТНАЯ МАТРИЦА
Определение. Обратной матрицей относительно данной квадратной невырожденной матрицы А называется такая квадратная матрица 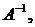 произведение которой на данную есть единичная матрица:
произведение которой на данную есть единичная матрица: 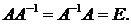
Вырожденная матрица 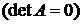 обратной не имеет.
обратной не имеет.
Любая невырожденная матрица имеет единственную обратную.
