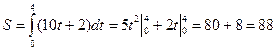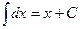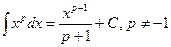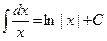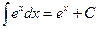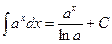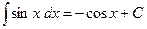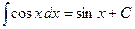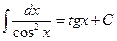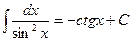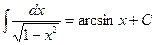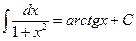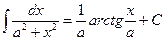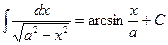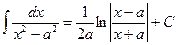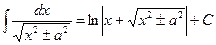Раздел 1. Основы математического анализа
Методические указания
К выполнению контрольных работ
По дисциплине
«МАТЕМАТИКА»
Для студентов заочного обучения
Для специальностей:, 270841, , 270802
С О Д Е Р Ж А Н И Е
Предисловие………………………………………………………………………… 2
Раздел 1. Основы математического анализа………………………………………. 3
Раздел 2.Основные численные методы……………………………………………. 10
Раздел 3. Элементы линейной алгебры…………………………………………….. 15
Раздел 4. Основы линейного программирования………………………………….. 20
Раздел 5. Основы теории множеств…………………………………………………. 27
Раздел 6. Элементы теории вероятности……………………………………………. 29
Рекомендуемая литература………………………………………………………….. 32
Предисловие
В настоящее время математика и ее методы широко используются при решении научно-технических проблем. Происходит математизация всех наук, математика глубоко проникает во все области деятельности современного человека. Математические методы позволяют решать проблемы планирования производства и расшифровывать древние рукописи, проверять качество проектов, прокладывать каналы и запускать космические корабли.
Математика является одной из таких наук, развитие которых служит необходимым условием ускорения научно-технического прогресса и повышения эффективности других наук.
Основная задача предмета «Математика» для средних специальных учебных заведений состоит в том, чтобы вооружить учащихся основами математических знаний, умений и навыков в объеме, необходимом для их повседневной практической деятельности, для усвоения общетехнических и специальных предметов, а также для дальнейшего повышения квалификации путем самообразования.
Раздел 1. Основы математического анализа
Тема 1.1.Функция. Предел функции.
Понятие функции важнейшее понятие математики вообще и центральное
понятие высшей математики.
Основным вопросом математического анализа является изучение зависимости между двумя или несколькими переменными при их совместном изучении.
Определение: Если в силу некоторого правила каждому значению переменной x из её области изменения соответствует одно определённое значение переменной у, то переменная у называется функция переменной х.
Область изменения аргумента х называют областью определения функции у.
Основные способы задания функции:
ü Аналитический (формула);
ü Графический;
ü Табличный .
Пусть дана функция y = f ( x ) .
Определение: Число А называется пределом функции y = f ( x ) в точке х=a, если для всех x сколько угодно мало отличающихся от a, т.е. (|x-a|<б), значение функции у сколь угодно мало отличается от числа А, т.е. (|y-A|<Е), т.е. если x→а, то 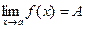
Свойство пределов:
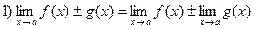
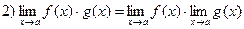
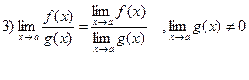
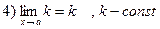
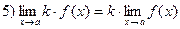
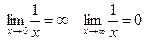
Примеры:
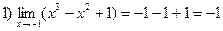
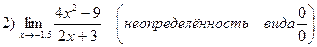
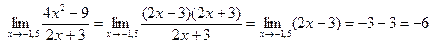
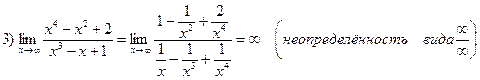
Функция y = f ( x ) называется непрерывной в точке х 0 , если она определенна в некоторой окрестности этой точки и если 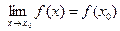
Тема 1.2. Производная и её приложения.
Пусть x1 и x2 – два значения аргумента, а y1=f(x1) и y2=f(x2) – соответствующие значения функции y=f(x).
Тогда разность 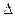 x=x2-x1 называется приращением аргумента, а разность
x=x2-x1 называется приращением аргумента, а разность 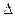 y=y2-y1= f(x2)- f(x1) приращением функции на отрезке [x1,x2]
y=y2-y1= f(x2)- f(x1) приращением функции на отрезке [x1,x2]
Определение: Производной функции y=f(x) по независимой переменной х при данном значении х (в данной точке х) называется предел отношения приращения 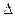 y функции y к вызывавшему его приращению
y функции y к вызывавшему его приращению 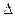 х независимой переменной х при стремлении
х независимой переменной х при стремлении 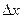 к нулю
к нулю
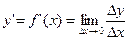
Если функция f(x) имеет производную в точке х, то она называется дифференцируемой в этой точке
Физический смысл производной функции
Задача. Пусть точка движется по прямой, и закон ее движения выражается зависимостью (функцией) пути от времени S=f(t)
Пусть в момент времени t точка занимает положение А; требуется определить её скорость в этот момент времени.
Перейдем для этого к моменту t1=t+ 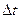 , когда точка займет положение В. Соответствующие приращение, т.е. путь, пройденный за промежуток времени
, когда точка займет положение В. Соответствующие приращение, т.е. путь, пройденный за промежуток времени 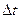 , выражается разностью
, выражается разностью 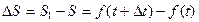
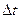 - промежуток времени, за который был пройден путь
- промежуток времени, за который был пройден путь 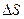 , тогда
, тогда 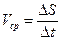 - средняя скорость за этот промежуток времени.
- средняя скорость за этот промежуток времени.
Пусть 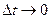 , тогда
, тогда 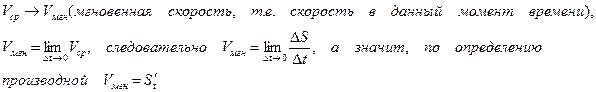
Производная пути по времени есть скорость в любой момент времени.
Пример:
 Дано: Решение:
Дано: Решение:

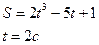
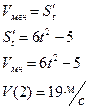
Найти: Vмгн
Правила и формулы дифференцирования

1) 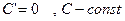
2) 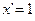
3) 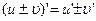
4) 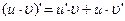
5) 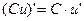
6) 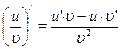
Производная сложной функции
Пусть y=f(и), где и- функция независимой переменной х: и=φ(х).
Тогда у=f(φ(х))- сложная функция, и - промежуточный аргумент.
Теорема: Если y=f(и) и и=φ(х) дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(х))существуют и равна произведению производной функции у по промежуточному аргументу и на производную промежуточного аргумента и по независимой переменной х: 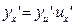
 |
7) 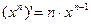 7а)
7а) 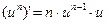
 8)
8) 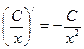 8а)
8а) 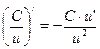
 9)
9) 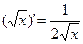 9а)
9а) 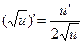

 10)
10) 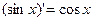 10а)
10а) 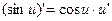
11) 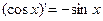 11а)
11а) 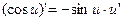
 12)
12) 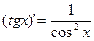 12а)
12а) 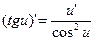
 13)
13) 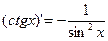 13а)
13а) 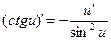
14) 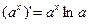 | 14а) 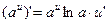 |
15) 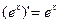 | 15а) 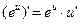 |
16) 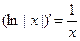 | 16а) 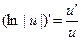 |
17) 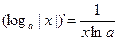 | 17a) 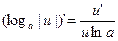 |
Формулы 7а, 8а, …….. 17а для сложных функций.
Примеры:
1) 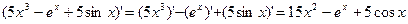
2) 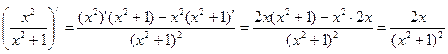
3) 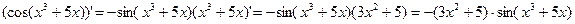
Вторая производная и производные высших порядков
Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее производной:
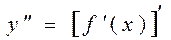
Производная n-го порядка (n-я производная) от функции y=f(x) есть производная от ее
(n-1)-й производной.
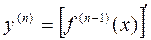
Тема 1.3. Интеграл и его приложения
Определение: Функция F(x) называется первообразной функции f(x) на интервале (a;в), если выполняется равенство F'(x)=f(x) Например:, первообразной функции y=x2, х R, является функция F(x)= 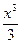 , т.к.
, т.к. 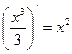 .Также
.Также  F'(x)=
F'(x)= 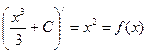
Определение: Множество всех преобразованных функций F(x)+С для f(x) называется неопределенным интегралом от функции f(x) и обозначается символом 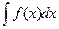
Таким образом, по определению 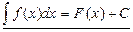 .
.
Основные свойства неопределенного интеграла:
1) 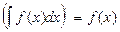
2) 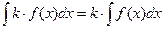
3) 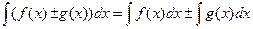
Основные формулы интегрирования.
Пример:
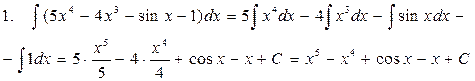
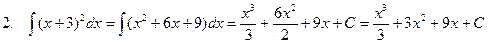
Интегрирование способом подстановки.
Пример: 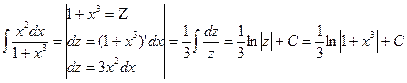
Определенный интеграл
Приращение F(в) – F(а) любой из первообразных функций F(x)+C при изменении аргумента от х=а до х=в называется определенным интегралом и обозначается:
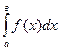
Т.е. 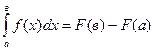
Для вычисления определенного интеграла 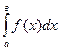 нужно наити соответствующий неопределенный интеграл, в полученное его выражение подставить вместо х сначала верхний, а затем нижний пределы определенного интеграла и из первого результата подстановки вычесть второй.
нужно наити соответствующий неопределенный интеграл, в полученное его выражение подставить вместо х сначала верхний, а затем нижний пределы определенного интеграла и из первого результата подстановки вычесть второй.
Решение прикладных задач с помощью определенного интеграла
Нахождение площади фигуры
Площадь фигуры, ограниченный кривой y=f(x), осью Ох и двумя прямыми х=а, х=в выражается определенным интегралом.
S= 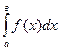




|
|


|
|


| |


Пример:
Определить площадь S фигуры, заключенной между графиком функции y=x2, осью Ох и прямыми х=0, х=3.
S= 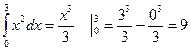
Нахождение пути, пройденного телом
Из физического смысла производной «скорость прямолинейного движения равна производной от пути по времени» т.е.
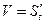
Интегрируя полученные равенство в пределах от t1 до t2, получаем
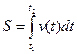
Пример: Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела v(t)=10t+2(м/с).
Решение: