Определение непрерывности функции

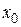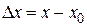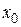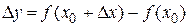Пусть на отрезке [a, b] задана функция y = f(x). Точки х и принадлежат интервалу (a, b). Разность называется приращением независимой переменной х в точке , а - приращением функции в точке 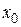при данном приращении Dх (рис. 9).

Пример 1.17. Найти приращения функций y = sinx и 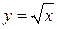в точке 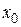при приращении аргумента .

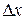Находим: 1) ;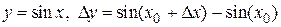

2) .

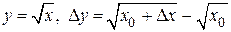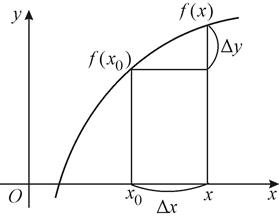
Рис. 9

Определение 1. Функция 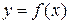называется непрерывной в точке 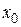, если она определена в окрестности этой точки и бесконечно малому приращению независимой переменной 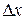соответствует бесконечно малое приращение функции Dy, т. е.

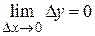. (1.4)

Например, функция y = С является непрерывной в любой точке хÎ(-¥ ; +¥), так как .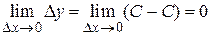

Функция y = х так же является непрерывной в любой точке хÎ(-¥ ; +¥), так как .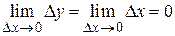

Преобразуем условие непрерывности (1.4)

.

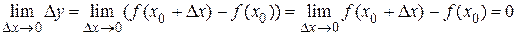Так как 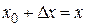, , 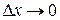то 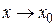. Учитывая это, получим

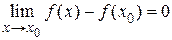или .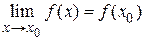

Последнее равенство можно записать следующим образом:

.

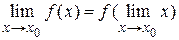Таким образом, если функция непрерывная, то предел от функции равен функции от предела независимой переменной, т. е. можно переходить к пределу под знаком непрерывной функции.

Определение 2. Функция 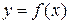называется непрерывной в точке 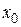, если она определена в окрестности этой точки и предел функции в этой точке равен значению функции в предельной точке, т. е.

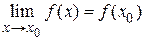. (1.5)

Определение 3. Функция 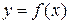называется непрерывной на отрезке [a, b], если она непрерывна в каждой внутренней точке этого отрезка и односторонние пределы функции в граничных точках равны значениям функции в этих точках, т. е. , .

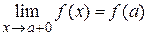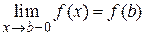Действия над непрерывными функциями

Теорема 1.11.Если функци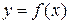и и 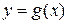непрерывны в точке 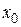, то в этой точке также непрерывны следующие функции:

1) ;

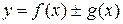2) ;

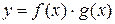3) 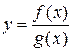, где .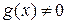

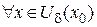Д о к о з а т е л ь с т в о. Используем второе определение непрерывности функции в точке и свойства пределов, получим:

1) ;

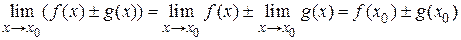2) ;

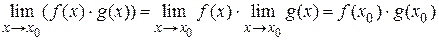3) .

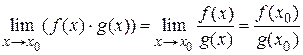Так как пределы от рассмотренных функций равняются значениям этих функций в предельной точке, то эти функции непрерывны.

Непрерывность элементарных функций

1. Многочлен 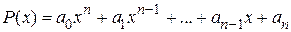является непрерывной функцией, так как он образован с помощью алгебраических действий сложения и умножения непрерывных функций: постоянных коэффициентов 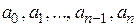и функции y = х (теорема 1.11).

2. Докажем, что функция y = sinx является непрерывной. Найдем

.

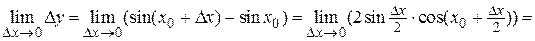
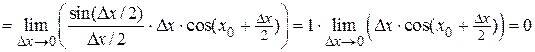Здесь использовали первый замечательный предел и то, что произведение бесконечно малой функции Dх на ограниченную функцию 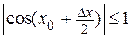является бесконечно малой. Так как 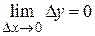, то по первому определению непрерывности функции функция y = sinx является непрерывной.

3. Докажем непрерывность функции y = lnx.

Найдем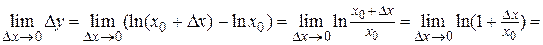

.

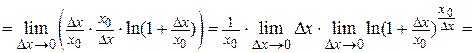
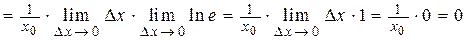Здесь был использован второй замечательный предел.

Аналогично можно доказать непрерывность других элементарных функций.