Определители третьего порядка

ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ

Методические указания к выполнению самостоятельной работы для студентов всех специальностей

Санкт-Петербург

УДК 519.95 (075.8)

Основы линейной алгебры: Методические указания к выполнению самостоятельной работы для студентов всех специальностей / Л.Е.Морозова, О.В.Соловьева. СПб. гос. архит.-строит. ун-т.- СПб., 2005. с.

Методические указания предназначены для самостоятельного изучения линейной алгебры студентами всех специальностей. Даны основные определения и теоремы теории матриц и определителей. Приводится методика решения систем линейных уравнений методом Гаусса.

Библиогр.: 4 назв.

Определители второго порядка.

Понятие определителя возникло в связи с проблемой отыскания формул для значений неизвестных в системе линейных уравнений.

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

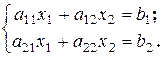
Таблица из коэффициентов вида 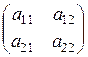называется матрицей системы.

Решим систему методом исключения. Чтобы найти неизвестное 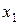, умножим первое уравнение на 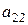, а второе - на 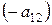и сложим оба уравнения. Получим

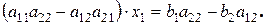
Аналогично, умножая первое уравнение на 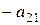, второе - на 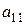и складывая оба уравнения, найдем

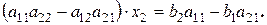
Коэффициент при 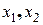называется определителем 2-го порядка и обозначается

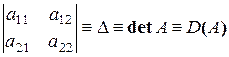, где

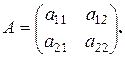
Таким образом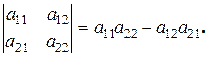

Пример1.1. Вычислить определители:

a) 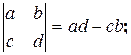b)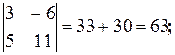

c)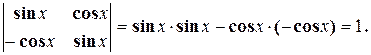

Определители третьего порядка.

Рассмотрим систему трех линейных уравнений с тремя не­известными:

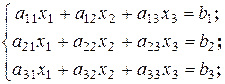
Матрица системы имеет вид: 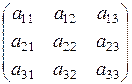. Решая систему методом исключения неизвестных, получим:

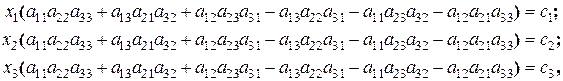
где 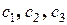- некоторые числа.

Определителем 3-го порядка называется коэффициент при неизвестных 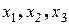и обозначается .

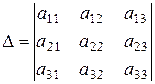Вычисляется определитель 3-го порядка по правилу Саррюса:

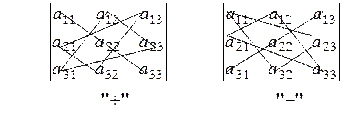
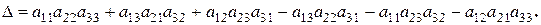
Величины 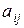- элементы определителя (матрицы). В определителе различают строки, столбцы, главную диагональ из левого верхнего угла и побочную диагональ из правого верхнего угла. Первый индекс элемента 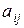указывает номер строки, второй – номер столбца.

Пример 2.1.Вычислить определитель по правилу Саррюса:

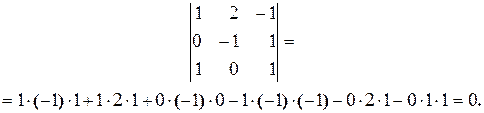
3.Элементарные сведения о перестановках.

Рассмотрим п целых чисел (элементов) 1, 2,..., п. Их можно располагать в различном порядке.

Определение 3.1: Всевозможные расположения чисел 1, 2, …, n называются перестановками. Переста­новка 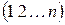, в которой числа идут в порядке возраста­ния, называется натуральной.

Пример 3.1. При п=3 возможны перестановки (1 2 3), (1 3 2), (2 1 3), (2 3I), (3 1 2), (3 2 1). Их число равно 3! = 6.

Определение 3.2: Факториалом n называется произведение первых n натуральных чисел.

n!=1∙2∙…∙n .

Принято считать 0!=1.

Методом математической индукции можно доказать, что из п элементов можно составить п!перестано­вок.

Определение 3.3:Назовем беспорядком(илиинверсией)в перестановке тот факт, что большее число стоит перед меньшим. Например, в перестановке (3 1 2 4) имеется два беспорядка; число 3 стоит перед числами 1 и 2.

Определим число беспорядков в перестановках из трех эле­ментов: в перестановке (1 2 3) — 0 беспорядков, (I 3 2) — 1, (2 1 3) — 1, (2 3 1) — 2, (3 1 2) — 2, (3 2 1) — 3.

Число беспорядков в перестановке может быть четным или нечетным. Перестановки с четным числом беспорядков назы­ваются четными, перестановки с нечетным числом беспорядков называются нечетными. Так, перестановки (1 2 3), (2 3 1), (3 1 2) четные, а перестановки (1 3 2),
(2 1 3), (3 2 1) не­четные.

Обмен местами двух элементов в перестановке называется транспозицией. Транспозиция переводит одну перестановку в другую. Одна транспозиция меняетчетность переста­новки, т. е. четная перестановка становится нечетной, а нечет­ная четной.

Для перестановки 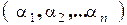количество беспорядков обозначают 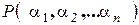, где 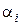-одно из чисел 1, 2,…, n ; 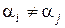, если .

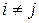Теперь отметим закономерности при вычислении определителя 3-го порядка.

1. Число слагаемых равно 6=3!, то есть равно числу перестановок из 3-х элементов.

2. Каждое слагаемое является произведением 3-х элементов 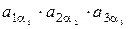, где перестановка первых индексов элементов – натуральная перестановка (1,2,3), а вторых индексов ( 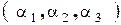)- некоторая перестановка чисел 1,2,3; таким образом элементы 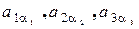из разных строк и столбцов.

3. Если перестановка 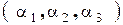четная, то слагаемое берется со знаком «+», а если нечетная, то со знаком «-».

Следовательно:

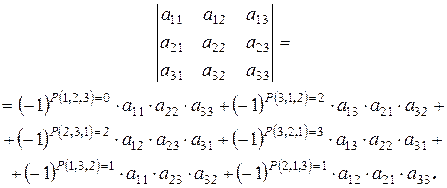
Для определителя второго порядка получим: