Указания по технике безопасности
1. Перед выполнением работы получите инструктаж у лаборанта.
2. Соблюдайте общие правила техники безопасности работы в лаборатории "Физика".
3. Осторожно обращайтесь с оборотным маятником. Не допускайте падений и ударов маятника, это может нарушить его регулировку.
Контрольные вопросы
1. Дайте определение колебательного процесса.
2. Перечислите параметры колебаний.
3. Дайте определения для основных параметров колебаний (амплитуда, частота, фаза, период).
4. Что такое гармонические колебания?
5. Что такое математический маятник?
6. Что такое физический маятник?
7. Что такое оборотный маятник?
8. Что называется приведенной длиной физического маятника?
9. Напишите уравнение движения при гармонических колебаниях.
10. Выведите формулу для периода колебаний математического маятника.
11. Выведите формулу для периода колебаний физического маятника
12. Покажите, что период колебаний физического маятника не зависит от его массы.
Лабораторная работа № 2
Измерение скорости тела методом баллистического маятника
 |
Цель лабораторной работы
Цель данной работы
заключается в изучении законов
сохранения количества движения и
полной механической энергии и их
применении при решении
практических задач.
Задачи лабораторной работы
Задачей работы является определение скорости шарика с помощью баллистического маятника.
Экспериментальное оборудование, приборы и принадлежности
Лабораторный стенд (рис.1) включает направляющую трубу (рис. 1-1) для фиксации траектории движения шарика, баллистический маятник с конусом — уловителем (рис. 1-2 и рис.2-1), датчик угла отклонения маятника на его оси (рис. 1-3 и рис.3), оптический датчик (рис. 1-4 и рис.2-2) для определения скорости вылета шарика.
 |
Рис.1
К приборам и принадлежностям относятся также компьютер с необходимым программным обеспечением, концентратор для подключения датчика к компьютеру и металлический шарик
(рис. 2-3).
Рис.2
Теоретическая часть
Вывод расчетной формулы основан на использовании законов сохранения полной механической энергии и сохранения момента импульса при неупругом ударе.
Ударом называется конечное изменение скоростей тел за весьма малый промежуток времени, происходящее при их столкновении.
В процессе деформации тел при ударе возникают мгновенные (ударные) силы, величина которых весьма значительна. Для системы соударяющихся тел эти силы являются внутренними. Их импульсы за время продолжительности удара называются мгновенными импульсами. Они во много раз больше импульсов за то же время всех внешних сил, приложенных к системе. Поэтому в процессе удара влиянием внешних сил можно пренебречь и считать, что система соударяющихся тел является замкнутой, т.е. з ней выполняется законы сохранения импульса (количества движения системы) и момента импульса.
Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругимназывается такой удар, при котором механическая энергия тел не переходит в другие, немеханические, вилы энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, причем тела разлетаются со скоростями, величина и направление которых определяются двумя условиями - сохранением полной энергии и сохранением полного импульса системы тел и момента полного импульса.
Абсолютно неупругийудар характеризуется тем, что потенциальной энергии деформации не возникает, кинетическая энергия тел полностью или частично превращается во внутреннюю энергию и после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь законы сохранения импульса и момента импульса, закон же сохранения механической энергии не соблюдается - имеет место закон сохранения суммарной энергии различных видов, механической и внутренней.
В момент попадания в неподвижный цилиндр баллистического маятника с конусом-уловителем шарик испытывает неупругий удар. После удара маятник с шариком начнет двигаться.
До момента попадания шарика в уловитель на систему не действуют никакие силы в горизонтальном направлении (в пренебрежении сопротивлением воздуха). Следовательно, момент импульса системы относительно оси вращения маятника остается постоянным.
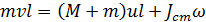 (1)
(1)
где т и M - массы шарика и уловителя; v и и - скорости шарика до столкновения и шарика вместе с уловителем после столкновения; l - длина
маятника; Jcm- момент инерции стержня 4 (рис.2), связывающего корпус уловителя с осью вращения маятника. Считая в первом приближении, что длина стержня равна расстоянию от оси до середины уловителя, т.е. l, воспользуемся формулой для оценки осевого момента инерции стержня относительно его торца:
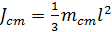 (2)
(2)
Здесь тст - масса стержня. Угловая скорость маятника после удара определяется из кинематики вращательного движения:
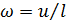 (3)
(3)
С учетом (3) после подстановки (2) в (1) получим выражение для скорости v:
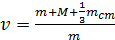 u (4)
u (4)
Кинетическая энергия вращательного движения системы после попадания шарика в цилиндр равна
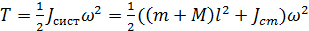 (5)
(5)
После подстановки выражений (2) и (3) получим:
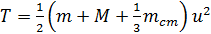 (6)
(6)
При последующем отклонении маятника в соответствии с законом сохранения механической энергии кинетическая энергия его движения переходит в потенциальную энергию сил тяжести. При максимальном его отклонении баланс энергий выглядит так:
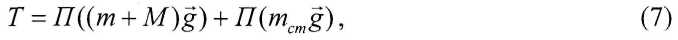
где П{(т + M)g) и П{mcmg) - потенциальные энергии сил тяжестей шарика с уловителем и стержня. Они определяются максимальным ростом их высот относительно своих нижних положений:
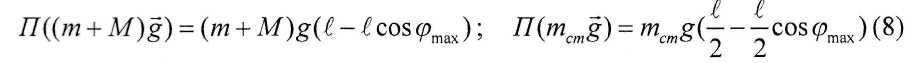
Во второй формуле в (8) введены коэффициенты 1/2 для учета положения центра тяжести стержня относительно оси вращения.
Приравняв правые части (6) и (7) с учетом (8), получим выражение для скорости движения маятника после столкновения и:
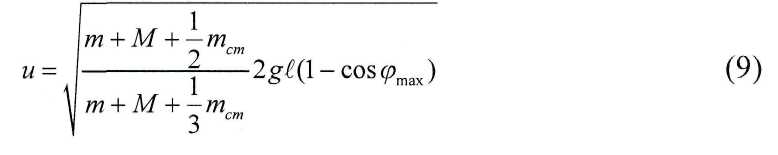
Воспользовавшись (4), можно получить расчетную формулу для определения скорости шарика:
