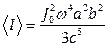Пространственно-временная дисперсия в электродинамике. Уравнения Максвелла для электромагнитного поля в среде с пространственно-временной дисперсией

Время релаксации 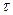- время установления равновесия при изменении поведения зарядов при наложении на систему зарядов внешнего поля.

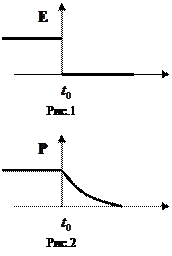
Включение или выключение поля не мгновенно изменяет состояние системы зарядов, а требуется некоторое время.

На рисунке 1 было поле 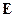, в момент времени 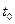поле отключили. Тогда на рисунке 2 приведено изменение поляризации системы.

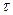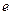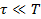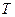- время, за которое исследуемая величина убывает в раз. Если , где - время, в течение которого поле меняется существенно, то можно считать, что исследуемая величина спадает мгновенно

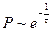
Но часто бывает иначе. Для описания того, что с исчезновением поля 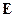величина 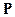спадает не сразу, используется временная дисперсия:

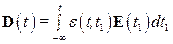
Если диэлектрические свойства стационарны по времени, то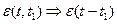

Для общего случая:

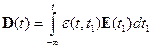, где 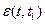- тензор

Аналогично, пространственная дисперсия – это влияние поля в соседних точках пространства на поляризацию в данной точке:

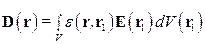
Для среды, однородной по диэлектрическим свойствам вводится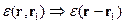

Размерность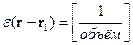

В общем случае имеем пространственно-временную дисперсию:

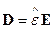
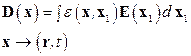
Интегрирование по 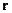по всему пространству, по 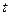на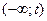

Для однородной стационарной среды:

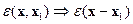
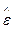- интегральный оператор, а 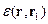- ядро этого интегрального оператора.

Запишем усреднённые уравнения Максвелла для среды:

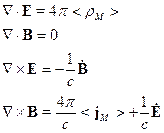(23.1)

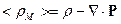, тогда первое уравнение переходит в .

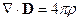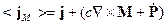
В случаях, когда пространственная дисперсия существенна (кристаллооптика для СВЧ полей) не удаётся измерить оба параметра 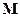и 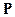, тогда удобно:

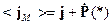- это для случая кристаллооптики с учётом пространственной дисперсии.

В этом случае четвертое уравнение из системы (1) принимает вид:

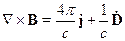
Это значит, что 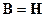, т.е. 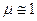и для описания среды остаётся только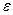

16 § 24. Волновое уравнение в случае среды с пространственной дисперсией

Запишем уравнения Максвелла для данного случая:

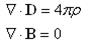
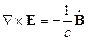(24.1)

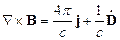(24.2)

и уравнение связи 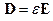. Если сторонних токов нет, то можно ещё привлечь закон Ома .

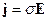Из (24.1) и (24.2) получим волновые уравнения. Подействуем операторами:

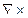на (24.1)

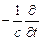на (24.2)

тогда получаем:

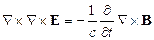(24.3)

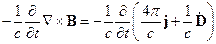(24.4)

Правая часть в выражении (24.3) и левая часть в выражении (24.4) совпадают, тогда:

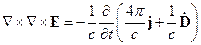(24.5)

(24.5) удобно записать в виде:

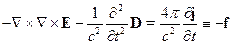
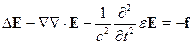
где 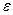- некоторый тензор.

Распишем в компонентах:

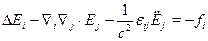
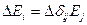, тогда

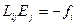
где оператор 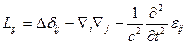- тензорный, дифференциальный оператор, он учитывает пространственную дисперсию.

Любое поле можно разложить по плоским монохроматическим волнам. Тогда решение уравнения 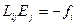сводится к нахождению и рассмотрению плоских монохроматических волн, этим плоским монохроматическим волнам соответствуют поля следующего типа:

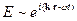
Разложение в интеграл Фурье:

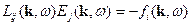
Операторы заменяем по правилу:

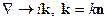
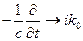
Последнее правило действует в случае плоских монохроматических волн. Тогда имеем выражение:

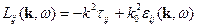
Здесь введён тензор 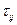, который определяется следующим образом:

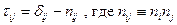
Решение уравнения 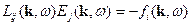зависит и от оператора в левой части, и от правой части. При 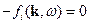мы имеем в решении нормальные волны (эти волны идут без источников).

17 § 25. Групповая скорость.

Фазовая скорость – это скорость распространения фронта волны. Если сигнал обрывается на каком-то моменте времени, то теряем монохроматичность. Тогда мы можем говорить о спектре частот, с несущей частотой 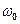и с разбросом частот .

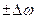Спектральную характеристику такого сигнала можно представить следующим образом:

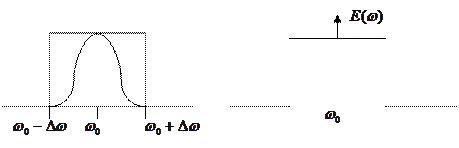Учитывая дисперсию среды (зависимость свойств среды от частоты), получаем искажение сигнала при прохождении среды. Каждая частота распространяется со своей скоростью в среде. Мы будем следить за распространением максимальной амплитуды.

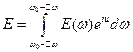, где фаза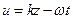

Зависимость 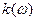означает дисперсию среды. Разложим 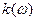в ряд:

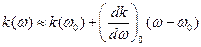
- такое разложение означает сильную дисперсию. Заметим, что 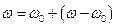. Разложим фазу 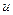в ряд по 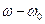до линейных слагаемых:

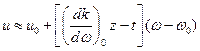
Считаем, что на краях интервала 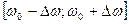сигнал спадает достаточно быстро:

,

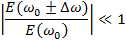
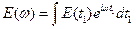
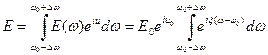где 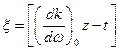, а 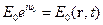. Тогда

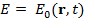
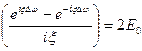
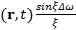
При 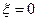имеем максимум амплитуды. Скорость перемещения максимума амплитуды находим из условия 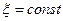, ξ = 0.

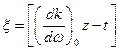
Тогда групповая скорость:

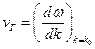
Фазовая скорость:

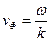
Групповая скорость – это скорость распространения сигнала. Найдём связь групповой и фазовой скорости:

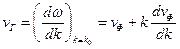
18 § 26. Метод самосогласования. Использование метода самосогласования для нахождения электростатического потенциала в плазме. Дебаевский радиус экранирования

Этот метод применяется тогда, когда задача достаточно сложна, но существует повторяющийся элемент в структуре задачи или существует статистическое усреднение.

Пусть 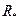- параметр, описывающий состояние среды в целом. Выделим элемент среды со свойствами 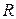(микросреда). Оставшемуся макрообъему приписываются свойства 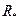. Тогда решают задачу

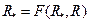
Мы получили самосогласованную задачу. Примером такой задачи может служить задача о расчете электрической цепи из бесконечно соединенных сопротивлений.

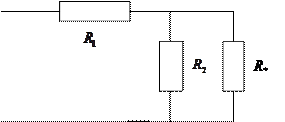
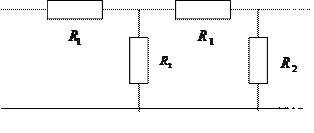
Метод самосогласования даст решение:

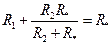
В плазме предполагаем сначала наличие частиц одного сорта. Вводим концентрацию частиц с номером 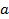в точке : .

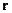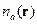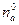- макроскопическое значение концентрации частиц.

Условие нейтральности означает:

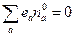
В некотором окрестном объеме суммарный заряд близок к нулю, но нулю не равен:

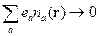
Концентрация заряженных частиц в различных плазмах (космическая, лазерная, и др.) разная и колеблется очень существенно:

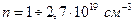
Часто накладывается ограничение: в плазме должно содержаться много частиц, чтобы проявлялись их коллективные свойства.

Используют формулу из статистической физики:

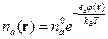
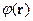- это электростатический потенциал.

Запишем уравнение Пуассона для электростатического потенциала в плазме:

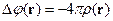
Используем идею самосогласования для электростатического потенциала.

Рассмотрим точечный заряд 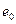в плазме, тогда 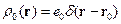. Запишем 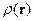всей среды – в ней надо учесть и 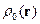и плотность зарядов остальной среды. Тогда

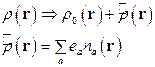
Используем формулу 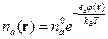. В экспоненте стоит потенциал 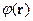, который и нужно найти. Для упрощения задачи разложим экспоненту в ряд. Если энергия электростатического взаимодействия во много раз меньше энергии теплового взаимодействия, т.е. плазма идеальная, то

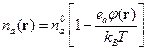
при условии, что 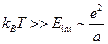(тепловое взаимодействие много больше электростатического).

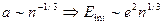
Условие идеальности плазмы принимает вид:

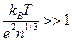
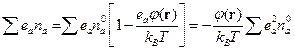
Тогда

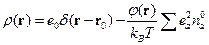
Подставим в уравнение Пуассона:

,

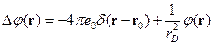где 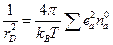, 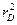- дебаевский радиус экранирования.

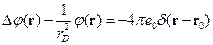
Мы получили уравнение Клейна, оно получается из уравнения Гельмгольца при замене 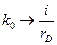. Решение уравнения Гельмгольца мы знаем:

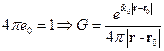- функция Грина

Тогда решение уравнения Клейна:

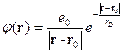
Часто пишут

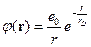
т.е. кулоновский потенциал, умноженный на экспоненту (влияние плазмы).

На расстоянии 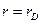от заряда потенциал убывает в е раз по сравнению с кулоновским и им пренебрегают. Потенциал экранируется зарядами противоположного знака из плазмы.

Для реализации коллективных свойств необходимо, чтобы концентрация частиц в объеме плазмы радиуса 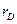была много больше единицы, т.е. .

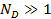Определение дебаевского радиуса экранирования было дано в предыдущем разделе:

(*)

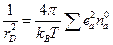С увеличение температуры радиус 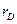растет, т.е. происходит размывание дебаевской области. Это происходит за счет теплового движения частиц в плазме.

Мы рассматриваем плазму, где нет столкновений между частицами. Опишем это качественно.

Пусть 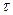- среднее время между столкновениями частиц. Плазма без столкновений – это плазма, в которой столкновения редки, по сравнению с параметрами поля. Пусть 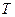- характерное время изменения поля, тогда

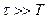или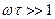

Наложим ещё одно условие. Пусть 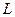- характерный размер, где расположена плазма, тогда:

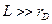
Так как эффекты, рассматриваемы нами, носят статистический характер, то число частиц в области радиуса 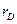должно быть достаточно большим, т.е. 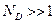. Оценим .

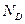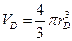, тогда ,

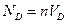здесь 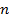- концентрация частиц в плазме, причем под 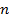понимают концентрацию разных частиц, например, может быть 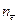. Под температурой 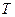понимают температуру электронного газа.

Если все заряды одинаковые, например, электроны, то 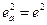. Тогда из формулы (*):

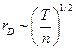
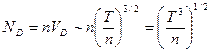
Условие идеальности плазмы 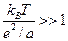дает нам ограничение:

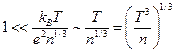
В результате получаем:

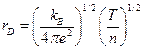и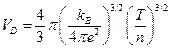

Обычно в плазме 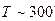К и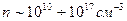

19 § 27. Запаздывающие потенциалы. Разложение запаздывающих потенциалов в ряды по малому параметру

Уравнения Даламбера для потенциалов в электромагнитном поле имеют вид:

ð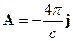

ð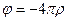

Здесь ð 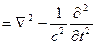- оператор Даламбера.

Для функции Грина в случае неограниченной среды имеем:

ð 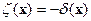, где 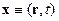- набор четырех переменных

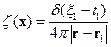- запаздывающая функция Грина

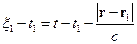или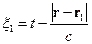

Тогда

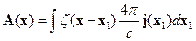
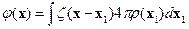
Используем свойство 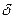-функции:

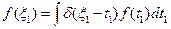
Получаем:

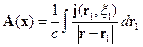
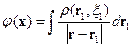
Мы получили частное решение уравнений Даламбера, т.е. реакцию среды на внешнее воздействие. Эти потенциалы – запаздывающие.

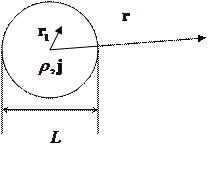
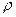и 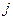- это источники поля. Рассмотрим поле на больших расстояниях.

Считаем, что выполнено условие:

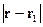
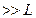
чем более точно оно выполнено, тем меньше нам нужно брать слагаемых в разложении. Запишем:

,

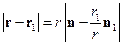где 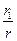- малый параметр, по которому производится разложение.

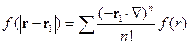
Разложим подынтегральные функции из 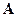и 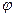в ряд Тейлора:

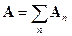
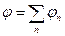
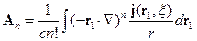
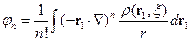
здесь 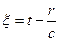, , 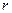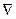от переменной интегрирования не зависят.

Рассмотрим .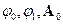

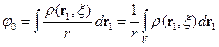
Здесь интегрирование ведется по всему объему системы с характерным размером .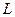

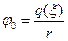- потенциал кулоновского типа

Зависимость 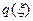- фиктивная, т.е. 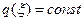. Обычно часть 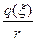не рассматривают, т.к. здесь не происходит излучения. Для излучения заряд должен двигаться ускоренно.

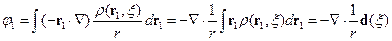
Дипольный момент зависит явно от переменной 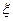, т.к. он берется в определенный момент времени ( 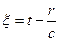). Тогда дипольный момент есть функция времени и координат.

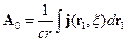
Интересно, что 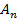и 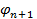связаны между собой калибровкой Лоренца.

20 § 28. Дипольное излучение. Волновая зона дипольного излучения

Дипольное излучение – это излучение системы, определяемое электрическим дипольным моментом.

Будем предполагать, что в выражениях для потенциалов учитываются только слагаемые, связанные с дипольным моментом:

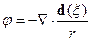
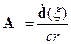
Потенциалы такого поля и приводят к излучению дипольного типа. Найдём напряженности электрического и магнитного полей:

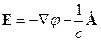
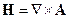
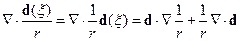
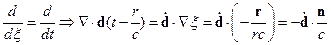
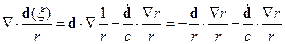
Множитель 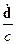имеет порядок .

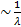Множитель 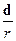имеет порядок .

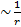Отсюда видим, что в от соотношения между 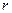и 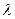мы можем пренебречь тем или иным слагаемым.

Рассмотрим следующие случаи:

1. Волновая зона дипольного излучения, т.е. r >> 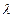, но r >>L (для наших разложений). Тогда r >> 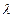>>L .

2. Ближняя зона, т.е. 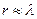, тогда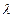 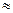r >>L

В волновой зоне 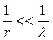и слагаемым 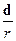можно пренебречь по отношению к 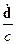и тогда:

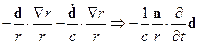
т.е. для волновой зоны .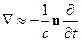

Для волновой зоны имеем условие .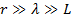

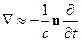
Тогда

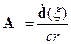
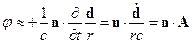
Т.е. 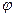- это продольная составляющая векторного потенциала.

Найдём напряженность электрического и магнитного полей.

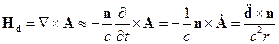
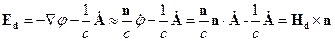
где 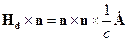. Тогда

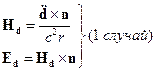
Дальше можно учитывать ещё слагаемые квадрупольного и других приближений.

Магнитный момент системы токов:

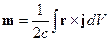
Если 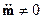, то можно говорить о магнитном излучении дипольного типа:

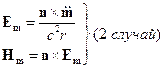
Можно так же учитывать слагаемые, связанные с излучением квадрупольного типа.

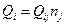
Тогда на базе тензора можно ввести вектор .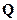

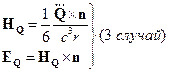
Размерность 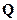на одну [длину] больше, чем размерность .

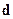(2 случай) и (3 случай) имеют один и тот же порядок малости и следующий по сравнению с (1 случаем), т.е.

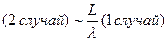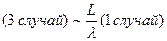и , где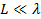

Соотношение 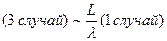следует из 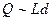, т.е.

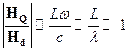
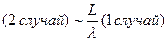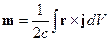
Рассмотрим соотношение . Здесь с учетом выражени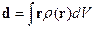й:

и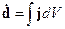

получаем:

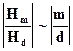
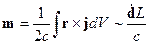
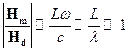
(2 случай) и (3 случай) надо учитывать, когда 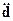- очень мало. Например, 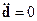для замкнутой системы зарядов, у которых .

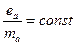21 § 29. Интенсивность дипольного излучения в волновой зоне. Примеры (задачи №23 и №28)

Поля 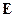и 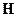для дипольного излучения в волновой зоне имеют вид:

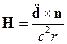
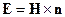
Интенсивность излучения – величина, определяемая через вектор Пойнтинга:

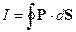- по замкнутой поверхности, охватывающей излучатель.

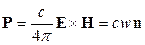, где 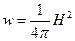- плотность энергии

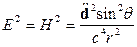
Угол 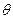- это угол, под которым наблюдают излучение.

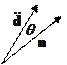
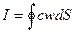
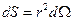
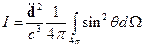
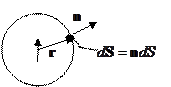
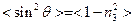
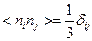, при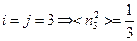

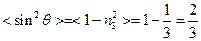
Тогда

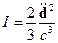
Пример 1.

Заряд, движущийся ускоренно:

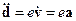
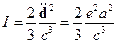
Эта формула справедлива для зарядов, движущихся с малыми скоростями 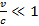. Если скорость заряда велика, то надо учитывать эффекты теории относительности, и вместо наших потенциалов надо использовать потенциалы Лиенара-Вихарта. Наш пример показал, что атом в классической теории не может быть устойчивой моделью.

Пример 2. Диполь Герца.

Дан кусок проволоки, в которой ток меняется по закону 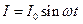. Рассчитать 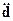можно, используя либо приближение линейного тока в тонких проводниках либо модель двух сфер, на которые подается пульсирующий заряд.

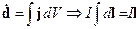
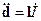
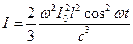
Средняя за период интенсивность составит:

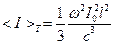
Пример 1 (задача №23)

Простейшая линейная антенна представляет собой тонкий прямолинейный провод длины l, по которому течет ток 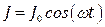. Определить интенсивность I длинноволнового излучения антенны в среднем за период колебания тока.

Решение

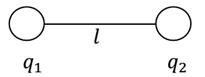
Пусть проводник соединяет две сферы. Заряд каждой сферы 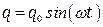. В этом случает ток 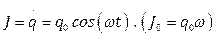. Таким образом, в целом, система представляет собой простейший диполь: 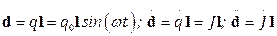. В результате интенсивность излучения такой системы равна:

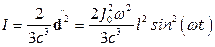
Интенсивность усредненная, за период колебаний тока 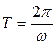, равна:

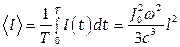
Ответ

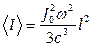
Пример 2 (задача №28)

Простейшая рамочная антенна представляет собой прямоугольную рамку со сторонами а и b, по которым течет ток 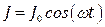. Определить интенсивность I длинноволнового излучения антенны в среднем за период колебаний тока.

Решение

По определению магнитный момент линейного тока: .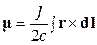
Т.к. 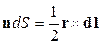, то 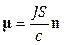, где площадь сечения S=ab, следовательно:

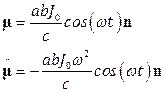
Отсюда интенсивность магнитно – дипольного излучения такой антенны равна:

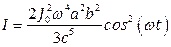
Интенсивность, усредненная за период колебаний:

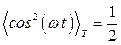
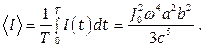
Ответ