Конспект лекций по обыкновенным дифференциальным уравнениям. ч.3. 1 страница

Федеральное АГЕНТСТВО СВЯЗИ

Государственное образовательное учреждение

высшего профессионального образования

Московский технический университет связи и информатики

А.Г. Кюркчан, Н.И. Смирнова

КОНСПЕКТ ЛЕКЦИЙ ПО ОБЫКНОВЕННЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ. Ч.3.

Учебное пособие

Москва 2011

УДК 517.9

Кюркчан А.Г., Смирнова Н.И. Конспект лекций по обыкновенным дифференциальным уравнениям. Ч. 3.: Учебное пособие/МТУСИ. – М., 2011 – с.

Предлагаемое учебное пособие предназначено, главным образом, для студентов, обучающихся по специальности «Прикладная математика», но может быть рекомендовано и студентам других специальностей. Оно составлено на основе существующей литературы по обыкновенным дифференциальным уравнениям, а также - методических разработок авторов. Курс дифференциальных уравнений входит в базовую часть перечня фундаментальных дисциплин образовательного стандарта по специальности «Прикладная математика». Для изучения этой дисциплины необходимы знания математического анализа и линейной алгебры, необходимо также уметь выполнять действия с комплексными числами.

Библиогр. 8 назв.

Рецензенты: д.ф.-м.н., профессор П.К.Суетин, МТУСИ,

д.ф.-м.н., профессор А.П.Анютин, РосНОУ.

Содержание

1. Понятие об устойчивости решений дифференциальных уравнений 4

1.1. Простейшие типы точек покоя 6

1.2. Замечания по поводу классификации точек покоя 10

1.3. Однородная система 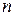линейных уравнений с постоянными коэффициентами 11

2. Теоремы Ляпунова об устойчивости 12

3. Исследование на устойчивость по первому приближению. 15

4. Дифференциальные уравнения с частными производными первого порядка 21

4.1. Первые интегралы систем дифференциальных уравнений 24

4.2. Характеристики 26

5. Линейные однородные дифференциальные уравнения в частных производных первого порядка с 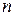независимыми переменными 28

6. Дифференциальные уравнения, допускающие понижение порядка 31

Список литературы 39

1. Понятие об устойчивости решений дифференциальных уравнений.

Исследование реальных явлений или систем обычно проводится при помощи математических модулей, при разработке которых исследование явления упрощается, идеализируется и т.п. При этом весьма важно, как влияют неучтенные факторы на решение.

Пусть некоторое явление или система может быть описана системой дифференциальных уравнений

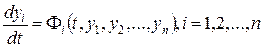(1)

с начальными условиями 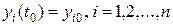, которые обычно задаются с некоторой погрешностью, т.к. полученное на основе эксперимента.

Если окажется, что сколь угодно малые изменения начальных данных могут сильно изменить решение, то такое решение не имеет никакой ценности, т.к. оно не может описывать изучаемое явление.

Если изменяется на конечном отрезке 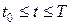, то в условиях справедливости теоремы существования и единственности решение непрерывно зависит от начальных значений и, следовательно, при малом изменении начальных значений решение изменится также мало.

Если же может быть сколь угодно большим, то на соответствующие вопросы ответ дает теория устойчивости.

Решение 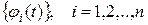системы (1) называется устойчивым по Ляпунову, если для 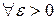можно подобрать такое 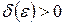, что для всякого решения 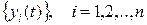, той же системы, начальные значения которого удовлетворяют неравенствам

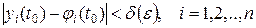
для всех 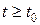справедливы неравенства

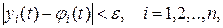(2)

т.е. близкие по начальным значениям решения остаются близкими при всех .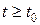

Если при сколь угодно малом 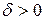хотя бы для одного решения 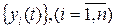неравенства (2) не выполняются, то решение 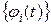называется неустойчивым.

Если решение 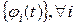не только устойчиво, но также удовлетворяет условию

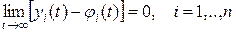(3)

когда 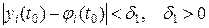, то решение 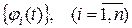называется асимптотически устойчивым.

Заметим, что из одного условия (3) ещё не следует устойчивости решения .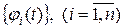

Пример.

Исследовать на устойчивость решение дифференциального уравнения 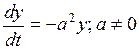, определенного начальным условием .

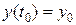Решение

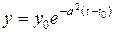
асимптотически устойчиво, т.к.

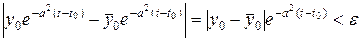
при 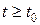, есл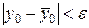и , и .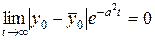

Исследование на устойчивость некоторого решения

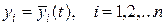
системы уравнений

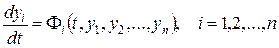(1)

Может быть сведено к исследованию на устойчивость тривиального решения – точки покоя, расположенной в начале координат.

Действительно, преобразуем систему уравнений (1) к новым переменным

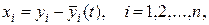(4)

где 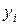– решение системы (1) с начальным условием 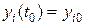. Новыми неизвестными функциями 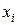являются отклонения 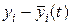“возмущенных” известных функций 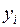от функций 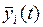, определяющих исследуемое на устойчивость решение.

При этом система (1) преобразуется к виду

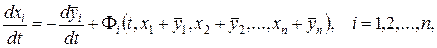(5)

или

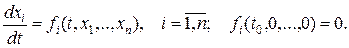(5а)

Очевидно, что исследуемому на устойчивость решению 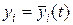системы (1), в силу зависимости 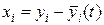соответствует тривиальное решение 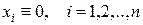, системы (5), удовлетворяющее нулевым начальным условиям 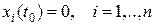, причем исследование на устойчивость решения 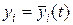системы (1) может быть заменено исследованием на устойчивость тривиального решения системы (5), т.е. расположенной в начале координат точки покоя системы уравнений.

Сформулируем условия устойчивости в применении к точке покоя .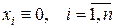

Точка покоя 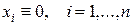системы (5) устойчива в смысле Ляпунова, если для каждого 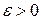можно подобрать 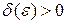такое, что из неравенства

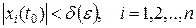
следует

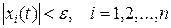при .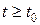

Иначе: точка покоя 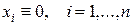устойчива в смысле Ляпунова, если для любого 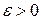существует 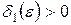, такое, что из неравенства

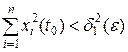
следует

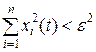
при 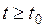, т.е. траектория, начальная точка которой находится в 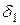окрестности начала координат, при 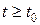не выходит за пределы 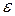– окрестности начала координат.

1.1. Простейшие типы точек покоя.

Исследуем расположение траекторий в окрестности точки покоя x=0, y=0 системы двух линейных однородных дифференциальных уравнений с постоянными коэффициентами.

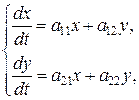(6)

где

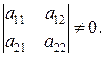
Решение ищем в виде 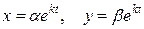. Тогда имеем характеристическое уравнение

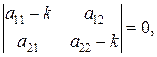
т.е.

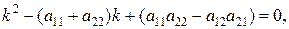
а 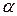и 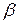с точностью до постоянного множителя определяются из одного из уравнений

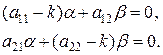(7)

Рассмотрим следующие случаи.

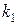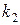а) Корни характеристического уравнения и действительны и различны.

Общее решение имеет вид

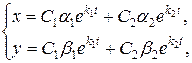
где 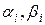– постоянные, определяемые из уравнений (7) соответственно 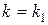при и при 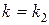, а 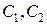– произвольные постоянные.

При этом возможны следующие случаи.

1) Если 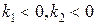, то точка покоя 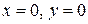асимптотически устойчива, т.к. из-за множителе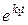й и 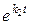в (8) все точки, находящиеся в начальный момент 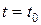в любой 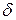- окрестности начала координат при достаточно большом переходят в точки, 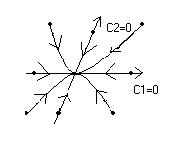достаточно большом переходят в точки, лежащие в сколь угодно малой 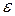– окрестности начала координат, а при 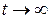стремятся к началу координат. Точка покоя рассматриваемого типа называется устойчивым узлом.

2) Пусть 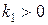и 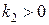. Этот случай переходит в предыдущий при замене на 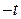. Следовательно, траектории имеют такой же вид, как и в предыдущем случае, но только точки по траекториям движутся в противоположном направлении. Очевидно, что с возрастанием точки, сколь угодно близкие к началу координат, удаляются из 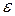–окрестности начала координат – точка покоя неустойчива в смысле Ляпунова. Такая точка покоя называется неустойчивым узлом.

3. Если 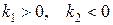, то точка покоя тоже неустойчива, т.к. движущаяся по траектории

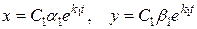(9)

точка при сколь угодно малых значениях 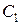с возрастанием выходит из 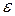– окрестности начала координат.

В рассматриваемом случае существуют движения, приближающиеся к началу координат, а именно

.

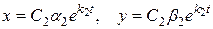При различных значениях 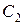получаем различные движения по одной и той же прямой

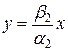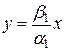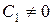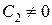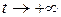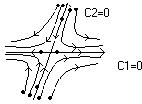
. При возрастании точки на этой прямой движутся по направлению к началу координат. Точки траектории (9) движутся с возрастанием по прямой , удаляясь от начала координат. Если же и , то как при , так и при 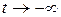траектория покидает окрестность точки покоя. Точка покоя рассматриваемого типа называется седлом, т.к. траектория в окрестности такой точки напоминают линии уровня в окрестности седловой точки поверхности .

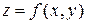б) Корни характеристического уравнения комплексные.

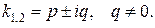
Общее решение системы (6) в этом случае можно представить в виде

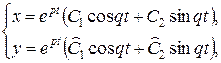(10)

где 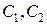– произвольные постоянные, а 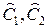– некоторые линейные комбинаци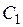и и 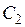. При этом возможны 3 случая:

1)

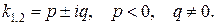
Множитель 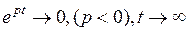, а второй - периодический множитель в соотношении (10) – ограничен. При 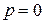траектории в силу периодичности вторых множителей в (10) были бы замкнутыми кривыми, окружающими точку покоя 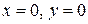. Из-за наличия множителя 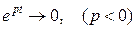при замкнутые кривые превра 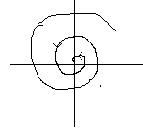щаются в спирали (направление закручивания траекторий определяется по вектору скорости 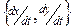в какой-либо точке 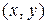), асимптотически приближающиеся при 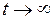к началу координат, причем при достаточно большом точки, находившиеся при 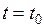в любой 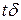- окрестности начала координат, попадают в заданную 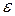– окрестность точки покоя 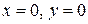, а при дальнейшем увеличении стремится к точке покоя. Следовательно, точка покоя асимптотически устойчива – это устойчивый фокус. Фокус отличается от узла тем, что касательная к траектории не стремится к определенному пределу при приближении точки касания к точке покоя.

2)

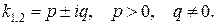
Этот случай переходит в предыдущий при замене на 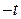. Следовательно, траектории имеют тот же вид, что и в предыдущем случае, но движение по ним при возрастании происходит в противоположном направлении (стрелки - от центра). Из-за наличия возрастающего множителя 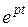точки, находившиеся в начальный момент сколь угодно близко к началу координат, с возрастанием удаляются из окрестности начала координат. Точка покоя неустойчива – это неустойчивый фокус.

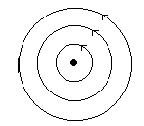
3)

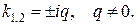
В этом случае траекториями являются, как отмечалось в пункте б)1), замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром. Центр является устойчивой точкой покоя. Т.к. для данной 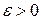можно подобрать 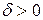такое, что замкнутые траектории, начальные точки которых лежат в 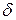– окрестности начала координат, не выходят за пределы 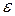– окрестности начала координат или, что то же самое, можно подобрать столь малые 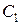и 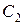, что решения

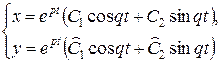(11)

будут удовлетворять неравенству

.

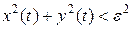Однако асимптотической устойчивости в рассматриваемом случае нет, т.к. 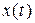и 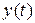в (11) не стремятся к нулю при .

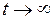в) Корни кратные .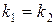

1) .

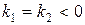Общее решение имеет вид

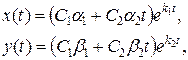
причем может быть 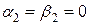, но тогда 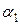и 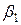будут произвольными постоянными, чтобы удовлетворить произвольным начальным условиям.

Из-за наличия множителя 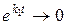при 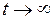произведение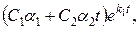 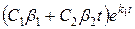стремятся к нулю при ,

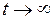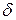причем при достаточно большом все точки любой – окрестности начала координат попадают в заданную 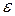– окрестность начала

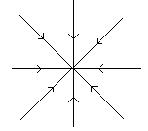
координат и, следовательно, точка покоя, асимптотически устойчива. Точка покоя рассматриваемого типа так же, как и в случае а)1) называется вырожденным устойчивым узлом. Этот узел занимает промежуточное положение между узлом а)1) и фокусом б)1), т.к. при сколь угодно малом изменении действительных коэффициентов 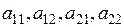он может превратится как в устойчивый фокус, так и в устойчивый узел типа а)1), ибо при сколь угодно малом изменении коэффициентов кратный корень может перейти как в пару комплексно сопряженных корней, так и в пару действительных различных корней. Если 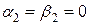, то тоже получается устойчивый узел - дикритический узел.

2) Если 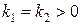, то замена на 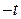приводит к предыдущему cлучаю, т.е. вид траекторий тот же, но движение происходит в противоположном направлении. В этом случае точка покоя, так же, как и в случае а)2) – неустойчивый узел.

Таким образом, исчерпаны все возможности, возникающие в случае 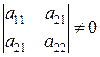, т.к. при этом характеристическое уравнение

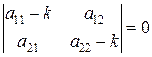
не имеет корней .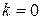

1.2. Замечания по поводу классификации точек покоя.

1) Если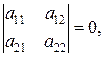

то характеристическое уравнение

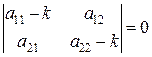
имеет нулевой корень .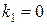

Предположим, что 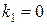, а 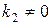. Тогда общее решение системы

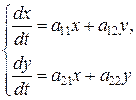(1)

Имеет вид

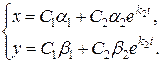
Исключая , получим семейство параллельных прямых

.

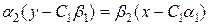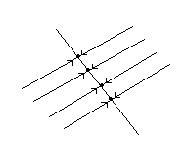При 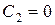получаем однопараметрическое семейство точек покоя, расположенных на прямой 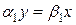. Если 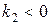, то при 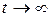на каждой траектории точки приближаются к лежащей на этой траектории точке покоя 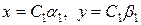. Точка покоя 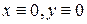устойчива, но асимптотической устойчивости нет. Если же 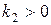, то траектории – те же, но движение по ним происходит в противоположном направлении – точка покоя 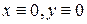неустойчива.